Podręcznik Grafika komputerowa i wizualizacja
Rozdział 4. PRZEKSZTAŁCENIA GEOMETRYCZNE
4.2. Przekształcenia 2D
Niech położenie punktu o współrzędnych (xp, yp) na płaszczyźnie reprezentuje wektor P :

Jeśli macierz M opisuje pewną transformację geometryczną to operację tę można opisać następująco:
![]()
czyli:
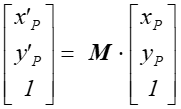
gdzie P’ opisuje położenie punktu po przekształceniu. Oczywiście, jeśli wynik mnożenia macierzy jest nieznormalizowany, to należy dokonać normalizacji.
Translacja.

Rys.4.2. Translacja o wektor na płaszczyźnie.
Jak opisać translację na płaszczyźnie?
Operację tę opisuje macierz
translacji 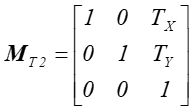 .
.
Między współrzędnymi zachodzi następujący związek:
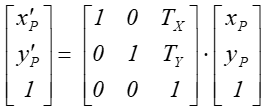
i jest to równoważne opisowi translacji o wektor w postaci układu równań:
 .
.
Symetrie osiowe.
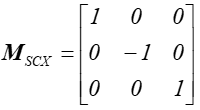

Rys.4.3 Symetria osiowa względem osi 0X.

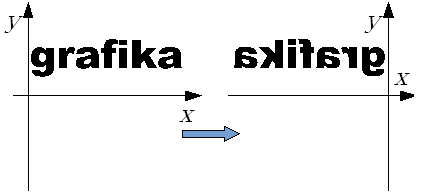
Rys.4.4 Symetria osiowa względem osi 0Y.
Symetria środkowa.
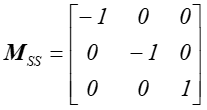
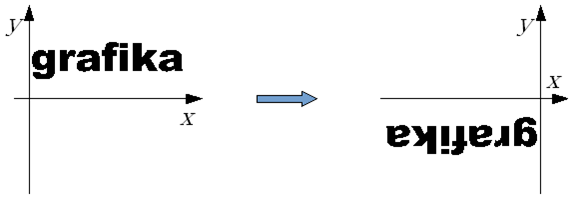
Rys.4.5
Symetria środkowa względem punktu [0,0] .
Obrót wokół początku układu współrzędnych.
 f
f 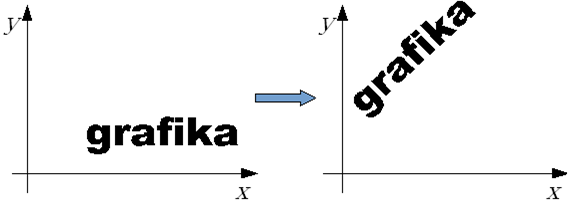
Rys.4.6 Obrót wokół początku układu współrzędnych o zadany kąt.
Skalowanie.

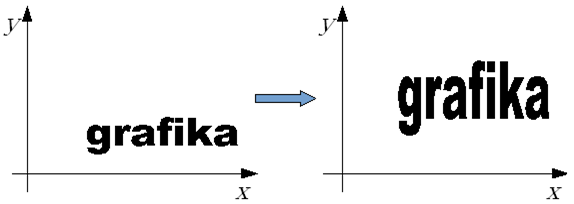
Rys.4.7
Symetria środkowa względem punktu [0,0] .
Skalowanie jest przykładem przekształcenia nieizometrycznego, to znaczy niezachowujacego odległości punktów.
Pochylenie.


Rys.4.8 Pochylenie:
zmiana współrzędnej y .


Rys.4.9 Pochylenie: zmiana współrzędnej x .
Pochylenie jest rzadziej stosowanym przekształceniem. Daje możliwość zniekształcenia figury. Nie zachowuje odległości punktów. Figura i jej obraz w tym przekształceniu nie są podobne.
