Podręcznik Grafika komputerowa i wizualizacja

Niech dane będą przekształcenia wykonywane kolejno M₁ i M₂  ,

czyli P' = M₁ · P   i   P'' = M₂ · P'  .

Podstawiając wynik pierwszej operacji do drugiego równania : P'' = M₂ · M₁ · P   .

Mnożenie macierzy jest operacją łączną więc :

                                                   P'' = M₂₁ · P  gdzie  M₂₁ = M₂ · M

Jeśli  zatem  M_C  opisuje całkowite przekształcenie będące wynikiem złożenia przekształceń elementarnych

  M₁ , M₂  , M₃ , . . . M_N         ( w takiej kolejności) to :

                                                    M_C = M_N · . . .  · M₃ · M₂ · M₁     

Oczywiście mnożenie macierzy jest operacją łączną ale nie jest operacją przemienną – złożenie najpierw translacji a potem obrotu jest innym przekształceniem niż złożenie najpierw obrotu a potem translacji.

 

Często pojawiającym się problemem w próbach implementacji przekształceń geometrycznych w grafice jest problem punktu odniesienia operacji.

Skalowanie jest operacją zmieniającą proporcje wymiarów względem początku układu współrzędnych. Punkt [0,0,0] jest punktem stałym tego przekształcenia. Wyobraźmy sobie dwukrotne powiększenie pewnego obiektu (np. powiększenie domu jak na rysunku 4.22). Powiększenie dwukrotne oznacza nie tylko, że zwiększą się wymiary obiektu. Oznacza również, że każdy punkt obiektu zwiększy dwukrotnie odległość od początku układu współrzędnych. A przecież obiekt jest „osadzony” w pewnych realiach sceny – np. wejście do domu jest w określonym miejscu. Prosta realizacja skalowania prowadzi do pewnych konfliktów. Aby tego uniknąć należy wybrać punkt obiektu, który powinien zachować współrzędne – punkt odniesienia. A następnie zrealizować skalowanie względem tego punktu odniesienia.  Efekt takiej (złożonej) operacji będzie uwzględniał uwarunkowania punktu odniesienia (rys. 4.23).

W przypadku skalowania złożenia operacji wygląda następująco:

1. Przesunięcie obiektu, aby punkt odniesienia znalazł się w początku  układu współrzędnych.
2. Skalowanie obiektu.
3. Przesunięcie odwrotne do operacji 1.

 

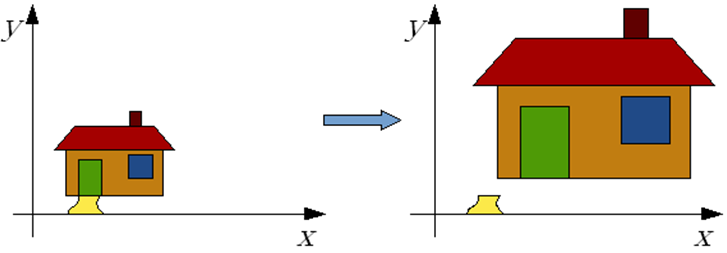
Rys.4.22. Skalowanie bez uwzględnienia punktu odniesienia.

   

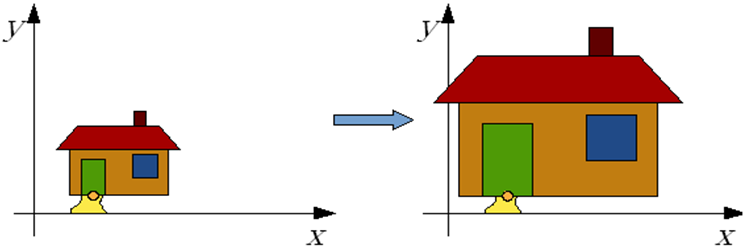
Rys.4.23. Skalowanie uwzględniające punkt odniesienia.

Jeśli macierz   M    opisuje pewną transformację geometryczną, przekształcenie współrzędnych jest opisane równaniem

                                                     P' = M · P     

i jeśli istnieje przekształcenie odwrotne opisane macierzą  M ^-1    to

                                                    P = M ^-1 · P' 

Oczywiście nie zawsze konieczne jest wyznaczanie macierzy odwrotnej, np. dla translacji o dany wektor przekształceniem odwrotnym będzie translacja o wektor przeciwny, dla obrotu o zadany kąt obrót wokół tej samej osi o kąt przeciwny itp.

Ponieważ symetrie, translacja, obroty i skalowanie opisane odpowiednimi macierzami są operacjami odwracalnymi, to w bardzo prosty sposób można pokazać, że dowolna operacja będąca złożeniem dowolnego zestawu tych operacji, jest też operacją odwracalną.

Jeśli zatem  M_C   opisuje całkowite przekształcenie będące wynikiem złożenia przekształceń elementarnych

                                               M_C = M_N · . . .  ·M₃ · M₂ · M₁

  i jeśli każde z nich jest odwracalne to :

                                               M_C^-1 = M₁^-1 · M₂^-1 · M₃^-1 · . . . · M_N^-1