Podręcznik Grafika komputerowa i wizualizacja

Niech X , Y  będą przestrzeniami metrycznymi z metrykami d_X, d_Y  (odpowiednio).

Niech ƒ: X → Y  będzie przekształceniem.

ƒ jest przekształceniem izometrycznym (izometrią) gdy   d_Y((f(p1),f(p2)) = d_X(p1,p2)

 Jeśli będziemy rozpatrywać przestrzeń Euklidesową oraz przekształcenia geometryczne w tej przestrzeni, to izometria będzie takim przekształceniem, które zachowuje odległości punktów.

 Bezpośrednio z definicji wynika również, że składanie izometrii jest także izometrią. Można wykazać, że w przestrzeni Euklidesowej  symetrie, translacje  i obroty są izometriami.

 W rozdziale tym przedstawione są różne (podstawowe) przekształcenia geometryczne opisane za pomocą rachunku macierzowego. Niech M będzie macierzą rozpatrywanego przekształcenia geometrycznego. Warto zadać sobie pytanie:

                                                           Jak sprawdzić czy przekształcenie to jest izometrią ???

 Pobieżna analiza zagadnienia może prowadzić do (częstego) błędu, że wystarczy obliczyć wyznacznik macierzy M i sprawdzić czy  det(M) = 1  (lub -1) . Jeśli sprawdzenie przyniesie pozytywny wynik to macierz M opisuje przekształcenie izometryczne. Niestety rozumowanie takie NIE JEST POPRAWNE.

Rozpatrzmy bowiem trzy przykładowe przekształcenia i macierze je opisujące:

                            skalowanie                                                                translacja                                                             pochylenie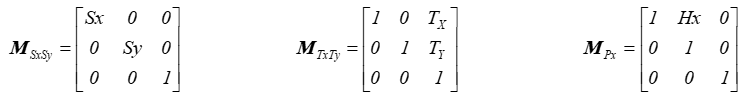

Jak łatwo obliczyć det(M_SxSy) = Sx ^.Sy  ,  det(M_TxTy) = 1  ,  det(M_Px) = 1  .  Oczywiście skalowanie nie zawsze jest przekształceniem izometrycznym (chyba że skala=1) i analiza problemu na podstawie wyznacznika dałaby poprawny wynik. Ale z pozostałych dwóch przekształceń tylko translacja jest izometrią. W przypadku pochylenia wynik jest BŁĘDNY.

 Jedyną  możliwością sprawdzenia czy przekształcenie jest izometrią jest porównanie odpowiednich odległości.

 Prawdziwe jest natomiast twierdzenie:

Jeśli przekształcenie opisane macierzą M jest izometrią   to  det(M) = 1  (lub -1) .

 

W praktyce stosując znane przekształcenia wykorzystujemy najczęściej twierdzenie, że składanie przekształceń izometrycznych jest izometrią. Stosując nieznaną macierz (macierz przekształcenia o nieznanych właściwościach) niestety pozostaje sprawdzić właściwości tego przekształcenia przez porównanie odległości odpowiednich punktów.