Podręcznik Grafika komputerowa i wizualizacja
Rozdział 4. PRZEKSZTAŁCENIA GEOMETRYCZNE
4.6. Przykład obrotu punktu wokół dowolnej prostej
Dana jest prosta 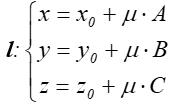
Na prostej tej
znajdują się dwa punkty T1 [x0,y0,z0] i T2 [x0+A,y0+B,z0+C],
wektor ![]() określa zorientowanie
prostej.
określa zorientowanie
prostej.
Zadanie: obrócić dowolny punkt P wokół prostej l o kąt![]() . (rys.4.24).
. (rys.4.24).
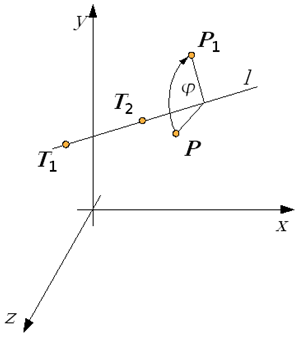
Rys.4.24. Zadanie: obrócić punkt wokół dowolnej prostej.
Zestaw podstawowych operacji obejmował obroty,
ale tylko wokół osi układu współrzędnych. Obrót wokół dowolnej osi musi być
zatem zrealizowany jako złożenie operacji. Można przyjąć założenie, że
generalnie celem operacji wstępnych jest takie przekształcenie przestrzeni, aby
zadana oś obrotu (prosta l na rysunku) pokryła się z wybraną
osią układu współrzędnych. Przy czym przyjęty zwrot osi obrotu powinien być
zgodny ze zwrotem osi okładu. Takie warunki pozwolą obrót o kąt ![]() wokół
zadanej osi zrealizować bezpośrednio jako obrót o kąt
wokół
zadanej osi zrealizować bezpośrednio jako obrót o kąt ![]() wokół osi układu.
wokół osi układu.
Zadanie można rozwiązać na wiele sposobów. Przyjęto następujący zestaw operacji:
- Przesunięcie, aby punkt T1 znalazł się w początku układu współrzędnych.
- Obrót wokół osi OX.
- Obrót wokół osi OY. Obroty (etap 2. i 3. ) zapewniają, że zadana oś obrotu (prosta l) pokryje się (z uwzględnieniem zwrotów) z osią OX układu współrzędnych.
- Realizacja zadanego
obrotu o kąt
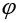 wokół
osi OX.
wokół
osi OX. - Obrót będący operacją odwrotną do operacji 3.
- Obrót będący operacją odwrotną do operacji 2.
- Przesunięcie odwrotne do przesunięcia 1.
Etap 1. Translacja o wektor [-x0, -yo, -zo]
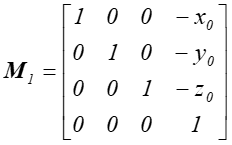
Rys.4.25 wynik pierwszej operacji – przesunięcia. Zadana oś obrotu zawiera teraz przekątną prostopadłościanu o bokach A, B, C. Ułatwi to definicje kątów obrotu.
Etap
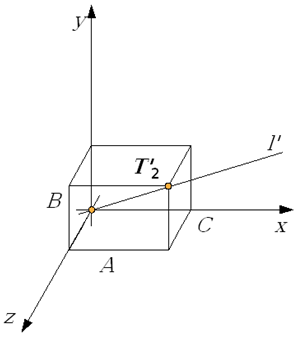
2. Obrót wokół oso OX i kąt ϕX taki,
że: ![]()
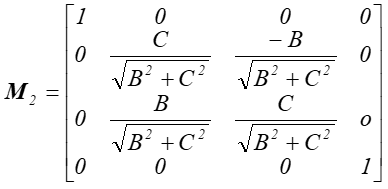
Rys.4.26 Po zrealizowaniu obrotu wokół OX prosta l znalazła się na płaszczyźnie XOZ.
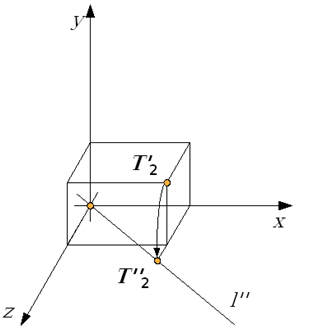
Etap 3. Obrót wokół osi 0Y o kąt kąt ϕY taki że: 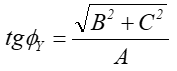
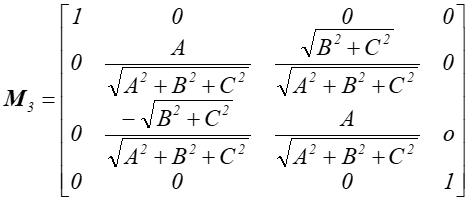
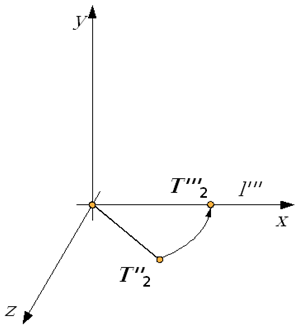
Rys.4.27 Po zrealizowaniu obrotu wokół OY prosta l pokryje się z osią OX układu współrzędnych. Jednocześnie odpowiednio dobrane operacje zapewniły zgodność zwrotów obu osi.
Etap 4. Obrót wokół osi OX o kąt ![]()
g 

Rys.4.28 Teraz
można wreszcie wykonać obrót o kąt ![]() wokół
prostej l co, dzięki odpowiednim operacjom wstępnym,
odpowiada obrotowi o kąt
wokół
prostej l co, dzięki odpowiednim operacjom wstępnym,
odpowiada obrotowi o kąt ![]() wokół osi OX układu współrzędnych.
wokół osi OX układu współrzędnych.
Następnymi etapami (5., 6., 7) będą operacje przeciwne do operacji 1., 2., 3. realizowane w odwrotnej kolejności.
Macierz przekształcenia całkowitego jest iloczynem macierzy opisujących przekształcenia odpowiadające kolejnym przedstawionym etapom.
A zatem macierz przekształcenia całkowitego jest opisana następującą zależnością:
MC = M1-1 · M2-1 · M3-1 · M4 · M3 · M2 · M1
