Podręcznik Grafika komputerowa i wizualizacja
Rozdział 4. PRZEKSZTAŁCENIA GEOMETRYCZNE
4.8. Kwaterniony
Kwaterniony (quaternions) są czterowymiarowym rozwinięciem liczb zespolonych, to znaczy można je traktować jako rozszerzenie do liczby o trzech składowych urojonych. q=s+ix+jy+kz (rys. 4.31). Kwaterniony zostały zaproponowane przez Williama Hamiltona w 1843 roku. Jako ciekawostkę warto dodać, że kwaterniony powstały jako kolejna próba rozszerzenia liczb zespolonych. Początkowo Hamilton próbował rozszerzenia z dwóch na trzy wymiary jednak okazał się, że jest to niemożliwe. Dopiero rozwinięcie czterowymiarowe okazało się dobrym rozwiązaniem. Hamilton wpadł na swój genialny pomysł przechodząc przez most w Dublinie. Przypomina o tym tablica (rys. 4.32).
Kwaternion może też być zapisany w postaci wektorowej jako:
![]()
gdzie ![]() .
.

Rys.4.31 Właściwości jednostek urojonych kwaterniona.

Fragment rysunku z Wikipedii (Autorstwa Cone83 - Praca własna, CC)
Rys.4.32 Tablica na moście w Dublinie upamiętniająca genialny pomysł Sir W.R Hamiltona.
Właściwości jednostek urojonych kwaterniona.
Dla dowolnego kwaterniona ![]() istnieje kwaternion przeciwny (sprzężony) o
postaci
istnieje kwaternion przeciwny (sprzężony) o
postaci ![]() .
.
Czyli ![]() .
.
Kwaternion przeciwny bywa
także oznaczany jako ![]() .
.
Można określić normę w postaci:
![]() .
.
Dla dowolnych kwaternionów p i q oraz liczby rzeczywistej a
![]() oraz
oraz ![]()
Kwaternion jednostkowy (jego norma jest równa 1)
![]()
Dla każdego kwaterniona ![]() różnego od zera istnieje kwaternion odwrotny
różnego od zera istnieje kwaternion odwrotny
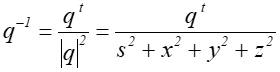
więc
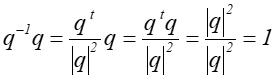 .
.
Zdefiniowane są też operacje dodawania i mnożenia kwaternionów.
Niech ![]() oraz
oraz ![]()
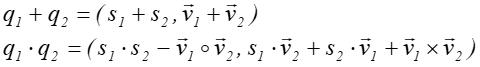
Dodawanie kwaternionów jest operacją łączną i przemienną.
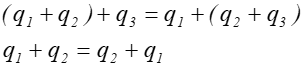
Mnożenie kwaternionów jest operacją łączną i nie jest operacją przemienną.

Kwaterniony są stosowane w teorii liczb i algebrze. Są bardzo użytecznym narzędziem do opisu zorientowania i obrotów. Stąd zastosowania w mechanice, robotyce i grafice komputerowej.
W grafice komputerowej kwaterniony są wykorzystywane w związku z jedną operacją w przestrzeni trójwymiarowej: z obrotem punktu wokół dowolnie zdefiniowanej osi.
Aby skorzystać z tej możliwości należy zdefiniować reprezentację punktu w postaci kwaternionu.
Dany jest punkt ![]() ,
odpowiada mu kwaternion
,
odpowiada mu kwaternion ![]() gdzie
gdzie ![]()
Niech jednostkowy
wektor ![]() reprezentuje oś obrotu w przestrzeni.
reprezentuje oś obrotu w przestrzeni.
Biorąc pod uwagę kwaternion jednostkowy postaci
![]()
związany
z tym wektorem jednostkowym, można wyznaczyć kwaternion ![]() o postaci.
o postaci.
![]()
Kwaternion ten reprezentuje punkt będący obrazem w
obrocie wokół osi wyznaczonej przez wektor ![]() o kąt
o kąt ![]() .
.
Aby dokonać obrotu punktu ![]() o kąt
o kąt ![]() wokół osi określonej przez wektor
wokół osi określonej przez wektor ![]() należy:
należy:
- wyznaczyć
kwaternion
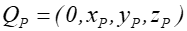 ,
, -
wyznaczyć kwaternion
 oraz
oraz  ,
, -
wyznaczyć kwaternion
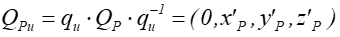 ,
, -
na podstawie
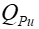 wyznaczyć
wyznaczyć 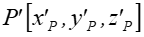 .
.
Porównując to rozwiązanie z zadaniem opisanym wcześniej widać prostotę operacji obrotu wykonywanej z wykorzystaniem kwaternionów.
Większość obrotów realizowanych w grach komputerowych jest wykonywana w taki sposób.
Więcej informacji na temat kwaternionów wraz z przykładami można znaleźć w pracach [2,4].
Problem obrotu w przestrzeni wokół dowolnie zdefiniowanej osi można rozwiązać korzystając z twierdzenia Eulera (rys.4.33).
Każdy obrót w przestrzeni może być opisany za pomocą trzech kątów w odpowiednim układzie współrzędnych.

Rys.4.33. Kąty Eulera definiujące dowolny obrót w
przestrzeni
Naturalną implementacją twierdzenia Eulera jest złożenie trzech macierzy
![]()
Takie podejście byłoby bardzo wygodne, gdyby nie problem niejednoznaczności, tzw. problem blokady przegubowej (gimbal lock). W trakcie realizacji tak zdefiniowanego obrotu może się bowiem zdarzyć, że dwie osie obrotu znajdą się na jednej prostej. Wtedy obrót wokół jednej osi wpływa na obrót wokół drugiej. Nazwa problemu pochodzi od mechanizmu przegubowego stosowanego np. do obsługi żyroskopu lub kompasu (rys.4.34), gdzie problem ten uniemożliwia jednoznaczne sterowanie urządzeniem.
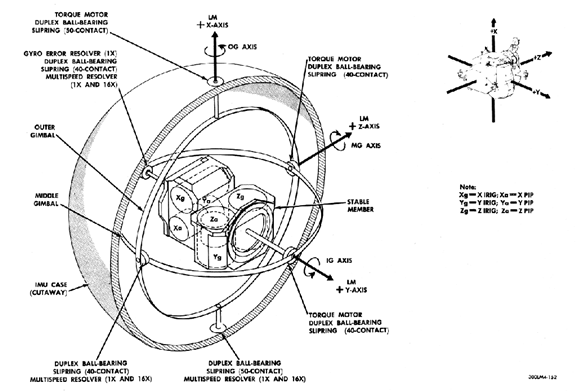
Rys.4.34. Przykład mechanizmu przegubowego do sterowania żyroskopem modułu księżycowego NASA. Rysunek pochodzi z Wikimedii (Public Domain) na podstawie https://www.nasa.gov/wp-content/uploads/static/history/alsj/lm10handbookvol1.pdf
Oczywiście stosując twierdzenie Eulera o trzech kątach w grafice komputerowej do opisania obrotów w zadanej sytuacji, można byłoby przewidzieć problem blokady przegubowej i zmienić warunki (np. kolejność operacji) aby nie dopuścić do niejednoznaczności. Niestety nie zawsze jest to wygodne, a często nie jest to możliwe, szczególnie w sytuacji interpolacji obrotu np. dla potrzeb animacji.
Realizacja obrotu z wykorzystaniem kwaternionów jest pozbawione tej wady. W tym przypadku definiowany jest od razu obrót wokół dowolnego wektora bez rozkładania na kolejne obroty składowe.
Podsumowując rozważania o kwaternionach warto porównać realizację obrotu za pomocą złożenia macierzy i operacji na kwaternionach. Tradycyjne składanie macierzy opisuje obrót w postaci sekwencji trzech, kolejno po sobie następujących operacji. Jest to podejście intuicyjne i łatwe w interpretacji. I niestety są to jedyne zalety. Składanie takie jest skomplikowane obliczeniowo. A przede wszystkim sekwencyjna realizacja obrotów może prowadzi do niejednoznaczności (gimbal lock). Tej podstawowej wady jest pozbawiona realizacja za pomocą kwaternionów, gdyż daje ona możliwość definicji obrotu bez rozbijania na składowe. Realizacja ta jest jednocześnie prostsza obliczeniowo. Jedyną wadą realizacji obrotów z wykorzystaniem kwaternionów jest złożona i trudna interpretacja operacji.
Więcej informacji na temat zastosowania kwaternionów i problemów związanych z obrotami można znaleźć w pracach [2,5,7].
