Podręcznik Grafika komputerowa i wizualizacja

Współczynnik sprzężenia można wyznaczyć na podstawie cząstkowych współczynników dla powierzchni elementarnych:    

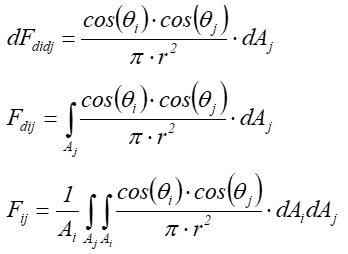
Współczynnik sprzężenia optycznego jest większy od zera jeśli powierzchnie „widzą się”, lub jest zerem gdy powierzchnie „nie widzą się”.

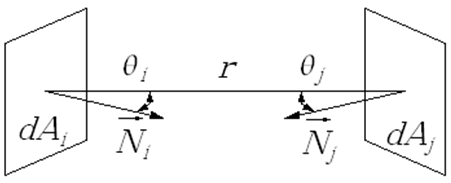
Rys.13.2. Wyznaczanie współczynnika sprzężenia optycznego.

Dla dowolnych powierzchni A_i oraz A_j

czyli

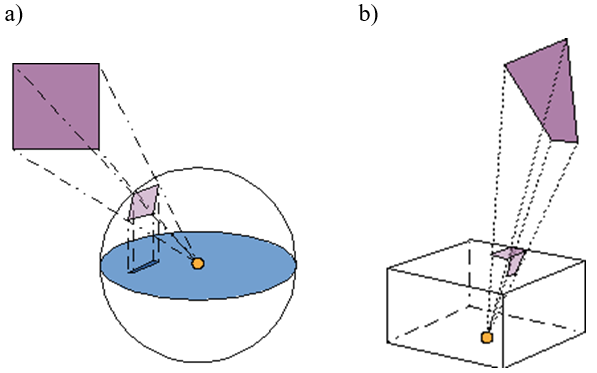
Rys.13.3. Wyznaczanie współczynnika sprzężenia optycznego. a) Rzut na półsferę – metoda Nusselta.
b) Rzut na półsześcian – metoda Cohena i Greenberga.

Współczynnik sprzężenia nie jest zależny od obserwatora, jest zależny natomiast  od właściwości powierzchni obiektów i ich wzajemnego ustawienia. Powinien być wyznaczony dla każdej pary powierzchni przed przystąpieniem do rozwiązywania układu równań bilansu energetycznego.

Zależności geometryczne współczynnika sprzężenia można opisać rzutując jeden z płatów na drugi. 
Pośrednio  jako:

W praktyce współczynnik sprzężenia bardzo rzadko jest liczony analitycznie.

Nusselt zauważył, że jeśli element i zostanie otoczony półsferą i dokonamy rzutu elementu j na tę półsferę, to z punktu widzenia oddziaływania w postaci współczynnika sprzężenia, obiekt j oraz jego rzut są równoważne. To znaczy, że obiekty mające taki sam rzut na półsferę maja takie same współczynniki sprzężenia.

Jeśli półsfera byłaby otoczona półsześcianem, to rzut na półsześcian tego samego obiektu byłby równoważny jego rzutowi na półsferę. Metodę opartą na tym spostrzeżeniu zaproponowali Cohen i Greenberg w 1985 roku.

W praktyce rzut na półsześcian okazał się najefektywniejszy obliczeniowo. Półsześcian dzieli się na powierzchnie elementarne (prostokątne „piksele”) i wyznacza współczynnik sprzężenia na podstawie rzutu obiektu na mapę pikseli półsześcianu.