Podręcznik Grafika komputerowa i wizualizacja

Reakcja światła z materią

Kolejnym problemem wymagającym rozwiązania, jeśli chcemy osiągnąć realizm rysunku, jest problem oświetlenia. Każda powierzchnia reaguje w jej właściwy sposób na padające na nią światło. Barwy, faktury i inne właściwości przedmiotów postrzegamy dzięki temu, że przedmioty te są oświetlone i odbijają światło w naszym kierunku. Symulacja tych zjawisk pozwala oddać realny wygląd elementów wirtualnej sceny.

Można wyróżnić dwa niezależne przypadki: odbicie światła i przenikanie światła (dla materiałów przezroczystych). Oczywiście może zachodzić jeszcze pochłanianie, ale z punktu widzenia obserwatora jest to najmniej interesujący przypadek. Dla przypadku odbicia mówimy o odbiciu kierunkowym (lustrzanym) lub rozproszonym (dyfuzyjnym). W pierwszym przypadku padający promień odbija się pod kątem równym kątowi padania. W drugim przypadku odbicie może być widoczne pod dowolnym kątem. Analogiczna sytuacja może zajść dla przenikania światła.

 

Właściwości reakcji na padające światło zależą od:

Rys.11.1.  Odbicie światła od powierzchni materiału:  a) .Odbicie kierunkowe idealne.
b) Odbicie kierunkowe rzeczywiste. c) Odbicie powrotne. d) Odbicie rozproszone.
e) Odbicie sumaryczne (wynikowe) rzeczywiste.

Odbicie rzeczywiste od powierzchni materiału jest zjawiskiem złożonym. Nawet dla najlepszych zwierciadeł promień odbity jest widoczny w pewnym niewielkim (niezerowym) kącie wokół kierunku odbicia idealnego (teoretycznego). W najprostszym przypadku wyróżnia się odbicie kierunkowe i rozproszone. Dla rzeczywistych powierzchni zawsze zachodzą oba przypadki i jednocześnie odbicie kierunkowe nie występuje w postaci idealnej. Dodatkowo może występować składowa odbicia powrotnego (współdrożnego) w kierunku, z jakiego padało światło. Można więc przyjąć rzeczywiste odbicie jako wypadkową 4 składowych (rys.11.1): rozproszonej, kierunkowej idealnej, kierunkowej rzeczywistej (ang. glossy – odbicia połysku), powrotnej. Analogiczne przypadki można wyróżnić rozpatrując załamanie promieni.

Rozkład kątów i wektorów związanych z odbiciem pokazano na rysunku 11.2.

 

Rys.11.2. Rozkład wektorów związanych z opisem odbicia światła  - wektor normalny do powierzchni w punkcie odbicia światła,     - wektory skierowane odpowiednio do obserwatora i do źródła światła,     - wektor idealnego odbicia,    - wektor wyznaczający dwusieczną kąta między   .

Anizotropia odbicia światła

Anizotropia jest zjawiskiem polegającym na zależności właściwości fizycznych od charakterystycznych kierunków materiału. Pojęcie anizotropii optycznej jest najczęściej kojarzone z przechodzeniem światła przez kryształy i zjawiskiem dwójłomności. Spowodowane to jest zależnością współczynnika załamania światła od kierunku rozchodzenia się fali względem głównego przekroju kryształu. Wyróżnia się anizotropię naturalną (wykazuje ją większość kryształów) i anizotropię wymuszoną, spowodowaną takimi czynnikami zewnętrznymi jak  działanie pól elektrycznych (zjawisko Kerra) i magnetycznych (zjawisko Cottona-Moutona) lub odkształcenia mechaniczne (ściskanie lub rozciąganie w zadanym kierunku). Z anizotropią mamy także do czynienia w przypadku odbicia promieniowania od powierzchni materiału. Wiele powierzchni, zarówno naturalnych, jak i uzyskanych w wyniku technologicznej obróbki odbija światło w sposób anizotropowy, zależny od kierunku jego padania – w sposób zależny od usytuowania powierzchni względem źródła światła. 

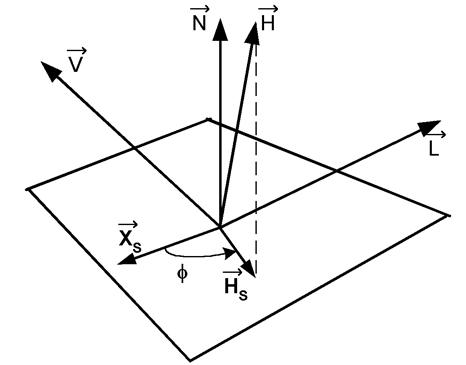
Rys.11.3. Anizotropia odbicia – rozkład wektorów.     - wektory jak na rysunku 11.2.
     - wektor określający charakterystyczny kierunek na powierzchni, 
   - rzut prostokątny wektora   na płaszczyznę styczną do powierzchni w punkcie odbicia światła.

Dobrym przykładem powierzchni wykazującej naturalne właściwości anizotropowe jest powierzchnia drewna. Odbija ona światło zależnie od kąta między kierunkiem padania a kierunkiem słojów przekroju. Powierzchnia metalu poddana obróbce mechanicznej (np. polerowaniu) będzie odbijała światło zależnie od kąta między padającym promieniem, a kierunkiem obróbki.

 

 11.1.3 Model odbicia Phonga

Najstarszy, z praktycznie wykorzystywanych w grafice komputerowej modeli odbicia, zaproponował Bui Tuong Phong w 1975 roku Model Phonga jest modelem eksperymentalnym, nieuzasadnionym fizycznie i niespełniającym zasady zachowania energii. Mimo to jest, chyba, najczęściej stosowanym modelem odbicia w grafice komputerowej, gdyż pozwala szybko uzyskać rysunki o wystarczająco realistycznych barwach. W literaturze są opisywane metody poprawy modelu Phonga, aby spełniał on zasadę zachowania energii.

Równanie oświetlenia ma w tym modelu postać:

 

gdzie  I  jest wynikowym natężeniem światła w punkcie analizowanego obiektu, I_a jest natężeniem światła otoczenia (tła),    I_p jest natężeniem światła punktowego,  k_a ,   k_d ,  k_s  -  są współczynnikami odbicia tła, rozproszonego i kierunkowego,      f_att jest współczynnikiem tłumienia źródła zależnym od odległości,   określa gładkość powierzchni – im wartość tego parametru jest większa, tym powierzchnia bardziej zbliża się do lustra idealnego.

 

Pierwszy składnik wzoru opisuje światło otoczenia (tła). Zakłada się, że jest ono rozproszone i bezkierunkowe oraz, że na skutek wielokrotnych odbić pada jednakowo pod wszystkimi kierunkami na rozpatrywane powierzchnie. Oczywiście również I_a jest jednakowe dla wszystkich obiektów.

Drugi składnik opisuje odbicie rozproszone tak zwane lambertowskie. Powierzchnie matowe; rozpraszające światło jednakowo we wszystkich kierunkach opisane są prawem Lamberta, zgodnie z którym światłość promieniowania odbitego jest proporcjonalne do kosinusa kata padania. Oczywiście rzeczywiste powierzchnie rozpraszające zachowują się zgodnie z tym prawem tylko w pewnym zakresie kąta. Niemniej jednak taki opis odbicia rozproszonego jest najczęściej stosowany w modelach odbicia.

Trzeci składnik opisuje odbicie kierunkowe (zwierciadlane). Maksimum natężenia promieniowania światłą odbitego występuje dla zerowego kąta α  natomiast potęga n we wzorze charakteryzuje właściwości odbiciowe danego materiału.

Warto jeszcze zwrócić uwagę na współczynnik tłumienia źródła światła. Wiemy z fizyki, że strumień światła pochodzący z punktowego źródła światła maleje z kwadratem odległości jaką przebywa. Zastosowanie tej reguły w modelu odbicia Phonga nie daje, niestety, w praktyce dobrych rezultatów. Dla dużych odległości od źródła zmiany są zbyt mało zauważalne, z kolei dla małych odległości zmiany występują zbyt szybko. Okazało się, że w praktyce dobre rezultaty można uzyskać dla współczynnika postaci  f_att=1/(c+r) gdzie c jest pewną stałą.

 

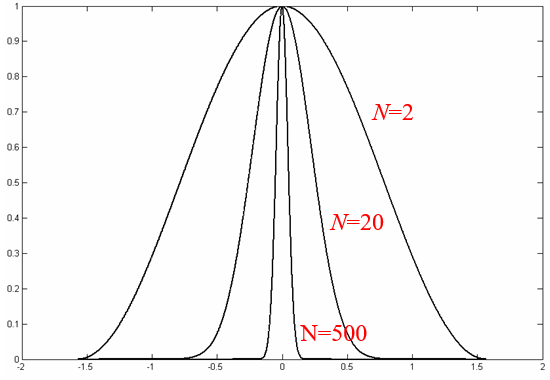
Rys.11.4.Wykres funkcji   f(α) = cos^N(α)  dla N=2, N=20 i N=500.

Funkcja f(α) = cos^N(α)  opisuje odbicie kierunkowe (zwierciadlane) przy czy N charakteryzuje dany materiał (właściwości odbiciowe powierzchni). Warto zwrócić uwagę na właściwości tej funkcji. Idealne odbicie kierunkowe to takie, w którym odbicie występuje tylko dla zerowego kąta a (to znaczy poza tym kątem natężenie światła odbitego jest zerowe). Funkcja f(α) = cos^N(α)  opisuje taki przypadek dla N dążącego do nieskończoności. Zatem im większa wartość N tym bardziej powierzchnia zbliża się do powierzchni lustrzanej. Tym lepsze właściwości kierunkowe charakteryzują odbicie od tej powierzchni. W praktyce już dla N rzędu kilkuset mamy do czynienia z bardzo dobrym lustrem.

 

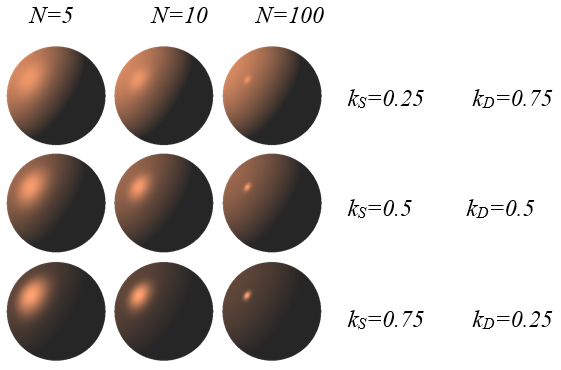
Rys.11.5. Kule o różnych właściwościach odbiciowych oświetlone źródłem punktowym.

 

Na rysunku 11.5 widać wpływ parametrów modelu odbicia Phonga na obraz odbicia światła na symulowanej powierzchni. Górny rząd charakteryzuje się przewagą odbicia rozproszonego, dolny – kierunkowego. Jednocześnie kolumny charakteryzują odbicie kierunkowe od lewej o złych parametrach odbicia kierunkowego (N=5) do prawej zbliżającej się do właściwości lustrzanych.