Podręcznik Grafika komputerowa i wizualizacja

Wybrane modele odbicia światła

 

W literaturze można wskazać wiele prac porównujących, przede wszystkim pod względem obliczeniowym, różne podejścia do opisu zjawiska odbicia. Znane funkcje BRDF można podzielić na dwie grupy : zależności opracowane eksperymentalnie i zależności mające podłoże fizyczne. Pierwszą grupę stanowią zależności, których opis matematyczny został eksperymentalnie dobrany do oczekiwanych (lub zmierzonych) efektów. Nie mają one żadnego uzasadnienia teoretycznego, ale są dobrą aproksymacją rzeczywistych zjawisk. Drugą grupę stanowią opracowania, które powstały na podstawie odpowiedniej teorii fizycznej opisującej gładkość (chropowatość) powierzchni. Obie jednak grupy są pewnym przybliżeniem rzeczywistości. Natomiast ze względów praktycznych nie zawsze jest celowe korzystanie z funkcji BRDF powstałych na podstawie pomiarów rzeczywistej powierzchni, gdyż jest to bardzo kosztowne obliczeniowo. Nawet w takich przypadkach stosuje się pewne aproksymacje . Warto więc zastanowić się nad wyborem odpowiedniej funkcji BRDF. Szczególnie jest to istotne w sytuacji prowadzenia obliczeń z wykorzystaniem gotowych pakietów numerycznych gdzie wybór dostępnych parametrów może być ograniczony.

 

Model Cooka-Torrance’a (1981 r.)

Zaproponowany przez Cooka i Torrance’a  w 1981 roku na podstawie wcześniejszych prac Torrance’a i Sparrowa dotyczących fizycznego opisu gładkości (chropowatości) powierzchni oraz  rozważań Blinna. Model Cooka-Torrance’a jest modelem uzasadnionym fizycznie, spełniającym zasadę wzajemności i zasadę zachowania energii, chociaż znane są w literaturze rozważania wskazujące na pewne problemy, które mogą się pojawić dla kątów padania promienia bliskich kątowi prostemu.

Funkcja BRDF opisująca odbicie kierunkowo-rozproszone w tym modelu jest dana zależnością:

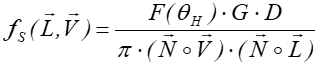
gdzie           jest współczynnikiem odbicia Fresnela opisującym zależność odbicia światła od kąta padania i od długości fali.

 G   opisuje tłumienie geometryczne. W modelu Cooka-Torrance’a założono, że powierzchnia materiału jest wielościanem złożonym z mikroelementów (mikroluster). Ich rozmiary i rozkład położeń decydują o chropowatości lub gładkości powierzchni. Przyjęto, że powierzchnia pokryta jest wgłębieniami typu V – to znaczy są to wgłębienia o kształcie ostrosłupa.

Tłumienie geometryczne jest wzajemnym zasłanianiem mikroelementów powierzchni i jest opisane następującą zależnością.

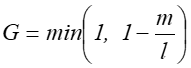
Biorąc pod uwagę rozkład wektorów i fakt, że analogiczne zasłanianie zachodzi przy zamianie źródła z obserwatorem (symetria) otrzymuje się:

                           

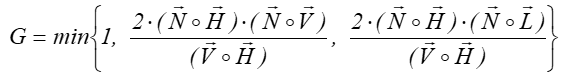
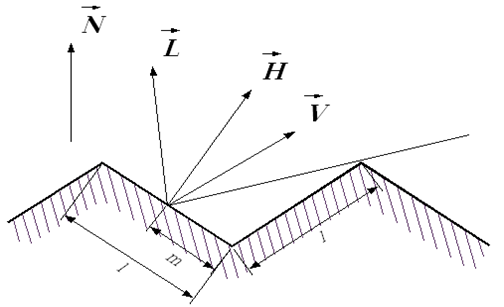
Rys.11.6. Tłumienie geometryczne – rozkład wektorów.

D   jest funkcją rozkładu mikroelementów tworzących powierzchnię . Cook i Torrance zaproponowali użycie funkcji rozkładu Beckmanna jako najbardziej odpowiadającej wielościennemu charakterowi powierzchni dla różnych materiałów:

                       

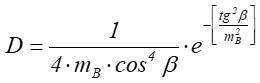
    opisuje właściwości powierzchni, im mniejsza wartość tym powierzchnia gładsza (odbicie bliższe idealnemu kierunkowemu).

 Znane jest również uproszczenie modelu Cooka-Torance’a - model Schlicka, zaproponowany w 1994 roku. Autor starał się dokonać uproszczenia z zachowaniem fizycznego charakteru modelu pierwotnego. Starał się jednocześnie znacznie podnieść atrakcyjność obliczeniową. W modelu Cooka-Torrance’a w równaniu zastąpione zostały wielkości G i D (funkcja rozkładu Beckmanna) prostszymi funkcjami wymiernymi.

 

Współczynnik Fresnela

Współczynnik Fresnela opisuje zależność odbicia światła od kąta padania i długości fali. Określa stosunek energii światła odbitego do energii światła padającego. Współczynnik ten jest wykorzystywany przez wszystkie modele odbicia opierające się na zależnościach fizycznych. Warto pamiętać, że kształt zależności kątowych tego współczynnika zależy od długości fali oraz polaryzacji światła.

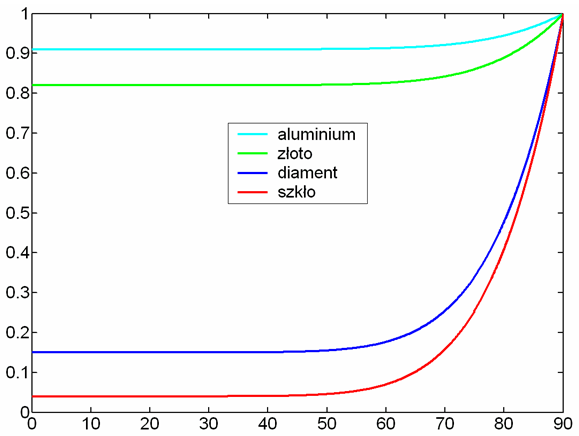
Rys.11.7. Przykłady współczynnika Fresnela      dla różnych materiałów. 
Prezentowane wykresy pokazują wartości średnie światła niespolaryzowanego.

Schlick zaproponował dobrą aproksymację tej funkcji (według autora aproksymacji błąd jest mniejszy niż 1%). Opisuje ją wielomianowa funkcja kąta i wartość współczynnika F₀ dla zerowego kąta oraz określonej długości fali. Wartości F₀ są podawane przez tablice materiałowe.

                

Funkcja rozkładu mikropowierzchni

O właściwościach kierunkowego odbicia w przyjętym modelu decyduje funkcja  D  rozkładu mikropowierzchni (czasami nazywana funkcją dystrybucji). Funkcja tego typu jest również wykorzystywana przez większość modeli odbicia. D  jest najczęściej funkcją kąta  β   lub kąta a (jak np.  w przypadku modelu Phonga) – rysunek 11.2. Spełnienie zasady zachowania energii wymaga, aby funkcja dystrybucji spełniała warunek normalizacji. Oznacza to dla powierzchni izotropowych następującą zależność:

            

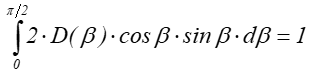
Autorzy funkcji dystrybucji nie zawsze dbali o spełnienie tego warunku. Czasem dopiero niezależne prace późniejsze doprowadzały do spełnienia zasady zachowania energii – tak było np. w przypadku modelu odbicia Phonga.

Istnieje wiele różnych funkcji dystrybucji – funkcji o podobnym charakterze – rys.11.8. Blinn w 1977 roku zasugerował możliwość zastąpienia jednej funkcji drugą. Czasami jest to opłacalne obliczeniowo, jednak może powodować powstanie drobnych różnic w rozkładzie światła symulowanego odbicia. Różnice te mogą być widoczne na rysunku.

 

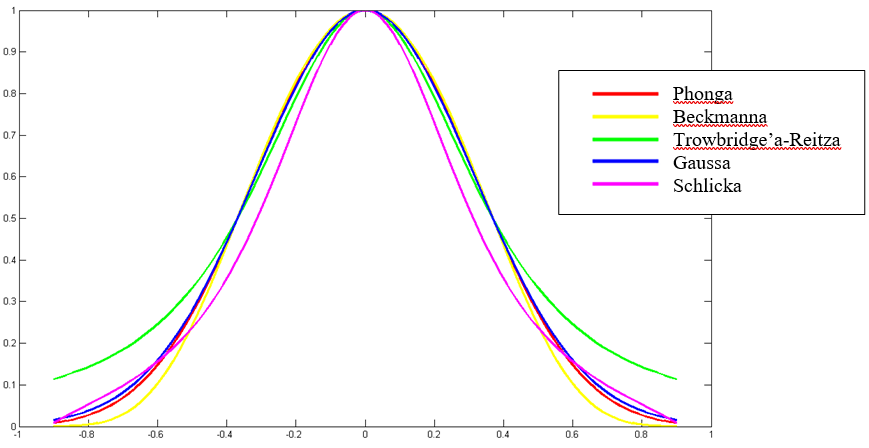
Rys.11.8 Wykresy znormalizowanych funkcji rozkładu mikropowierzchni.

 Na rysunku 11.8 są pokazane różne funkcje rozkładu mikropowierzchni w postaci znormalizowanej (oznaczone jako)   tzn. takie, że  .  Normalizacja pozwala porównać właściwości różnych funkcji.  Dla większości funkcji dystrybucji (wszystkich tutaj rozpatrywanych) jej maksimum występuje dla  β = 0 .

W pracy [9] przedstawiono różne funkcje rozkładu mokropowierzchni. Można przeczytać o ich właściwościach oraz możliwościach zastąpienia jednej funkcji drugą oraz konsekwencjach wizualnych takiego zastąpienia.

Model Warda (1992 r.)

Model Warda zaproponowany w 1992 roku  uwzględnia anizotropię odbicia światła. Jest to jeden z pierwszych tego typu modeli i jednocześnie jest on nadal często używany – jest często dostępny w gotowych pakietach oprogramowania.

Model Warda niestety nie uwzględnia współczynnika Fresnela, co nie daje możliwości opisania w pełni właściwości materiałowych i uwzględnienia zależności kątowych. Jest to szczególnie widoczne dla dużych kątów padania światła. Składowa kierunkowa (kierunkowo-rozproszona) jest wyrażona w tym modelu wzorem:

 

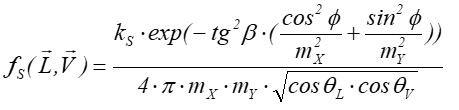
k_s   - jest współczynnikiem materiałowym,   m_x  oraz  m_y  opisują gładkość niezależnie wzdłuż kierunków prostopadłych powierzchni

 

Model Orena-Nayara (1994 r.)

Oren i Nayar zwrócili uwagę na rozkład postrzeganej luminancji na rzeczywistych powierzchniach rozpraszających. Zastosowanie modelu odbicia Lambertowskiego (opisu idealnego odbicia rozproszonego), tak jak w większości modeli oświetlenia, powoduje. że efekt często całkowicie odbiega od rzeczywistego. Jest to spowodowane przede wszystkim rzeczywistym odbiciem rozproszonym, które odbiega od modelu Lambertowskiego. Rzeczywiste obiekty (np. porcelana nieszkliwiona) odbijają w taki sposób, że dla dużych kątów padania światła luminancja odbicia jest większa niż w modelu Lambertowskim.

W modelu Orena-Nayara funkcja opisująca odbicie rozproszone (dyfuzyjne) ma postać:

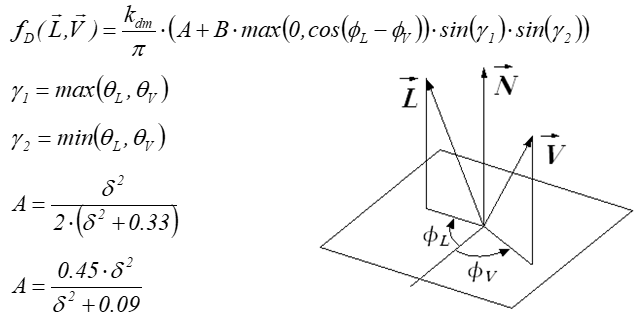
k_dm    jest współczynnikiem odbicia rozproszonego,   d   jest stałą materiałową.

Oren i Nayar opracowali model, w którym przybliżyli powierzchnię obiektu powierzchnią wielościenną. Założyli, że obiekt pokryty jest wgłębieniami typu V podobnie jak w modelu Cooka-Torrance’a. Przy czy w modelu Orena-Nayara mikropowierzchnie nie są lustrzane ale rozpraszają w sposób lambertowski. To znaczy dla każdej pojedynczej mikropowierzchni jest stosowany Lambertowski model odbicia.

Dla takiego modelu powierzchni zastosowali rozkład Gaussa kierunku wektora normalnego do powierzchni wielościennej. W efekcie uzyskali model uwzględniający wzajemne zasłanianie powierzchni wielościennej typu V ale przy lambertowskim odbiciu od mikropowierzchni. Ponieważ uzyskany opis był zbyt skomplikowany do zastosowań praktycznych, zaproponowali aproksymację prostymi równaniami.

 

Model Ashikhmina-Shirleya (2000r.)

Model Ashikhmina-Shirleya jest współczesnym modelem odbicia. Jest on niejako rozszerzeniem modelu Phonga, ale spełnia on wszystkie podstawowe wymagania (zasada wzajemności, zasada zachowania energii, uwzględnia współczynnik Fresnela odbicia światła). Odbicie kierunkowe w tym modelu opisuje równanie:

 

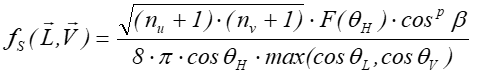
przy czym    ,  gdzie współczynniki  n_u   oraz   n_v  opisują gładkości niezależnie wzdłuż odpowiednich prostopadłych kierunków powierzchni – im większa wartość tym powierzchnia gładsza.

Model został sformułowany w taki sposób, że może być wykorzystywany w dowolnych obliczeniach graficznych – także we wszystkich wariantach metody śledzenia promieni.  Pozwala także uwzględnić anizotropię odbicia pokazaną na rys. 11.9.

 

Rys.11.9. Rysunki kul o powierzchniach charakteryzujących się  anizotropią odbicia,
wartości współczynników we współrzędnych sferycznych    .

 W modelu Ashikhmina-Shirleya opisano także odbicie rozproszone. Przy czym opisano je w sposób bliższy zmianom rzeczywistym niż uwzględnia teoretyczny opis Lamberta.

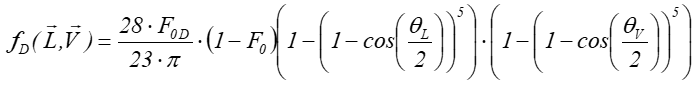
F₀ — współczynnik Fresnela dla zerowego kąta,

F_0D — współczynnik Fresnela dla zerowego kąta dla odbicia dyfuzyjnego.

 

Jednocześnie trzeba podkreślić, że jest to inne podejście do opisu odbicia rozproszonego niż w modelu Orena-Nayara. W modelu Ashikhmina-Shirleya wykorzystano opis oparty na pomyśle Schlicka aproksymacji wielomianowej.

Model Ashikhmina-Shirleya ma dodatkowo jeszcze jedną zaletę: jest modelem atrakcyjnym obliczeniowo.

 

Model He-Torrance’a-Silliona-Greenberga (1991 r.)

 Model He-Torrance’a-Silliona-Greenberga został opracowany jako rozszerzenie modelu Cooka-Torrance’a.

Jest to najpełniejszy ze znanych modeli odbicia, uwzględnia praktycznie wszystkie znane zjawiska fizyczne z tym związane (polaryzację, dyfrakcję, interferencję). Ma tylko jedną wadę: jest całkowicie niepraktyczny, czas obliczeń może być kilkaset (100 – 300) razy dłuższy w stosunku do innych opisywanych tutaj modeli. Dodatkowo, ze względu na sposób prowadzenia obliczeń nie może być wykorzystywany w algorytmach typu Monte-Carlo. Złożoność modelu uniemożliwia również jego prostą prezentację.

 

Porównanie właściwości

Na rysunku 11.10 przedstawiono zmianę kształtu funkcji odbicia w zależności od kąta padania światła dla przykładowych wartości parametrów. Aby możliwe było porównanie różnych modeli odbicia przeprowadzono przeliczenie parametrów między modelami w taki sposób, aby uzyskać zgodność dla kątów odpowiadających połowie wartości funkcji. – Takie postępowanie opisał Blinn w 1977 roku dla funkcji rozkładu mikropowierzchni. Jednocześnie dokonano normalizacji funkcji dla zerowego kąta padania światła. Dzięki temu możliwe staje się zastąpienie jednej funkcji drugą. Możliwe jest także porównanie kształtów – właściwości poszczególnych funkcji.

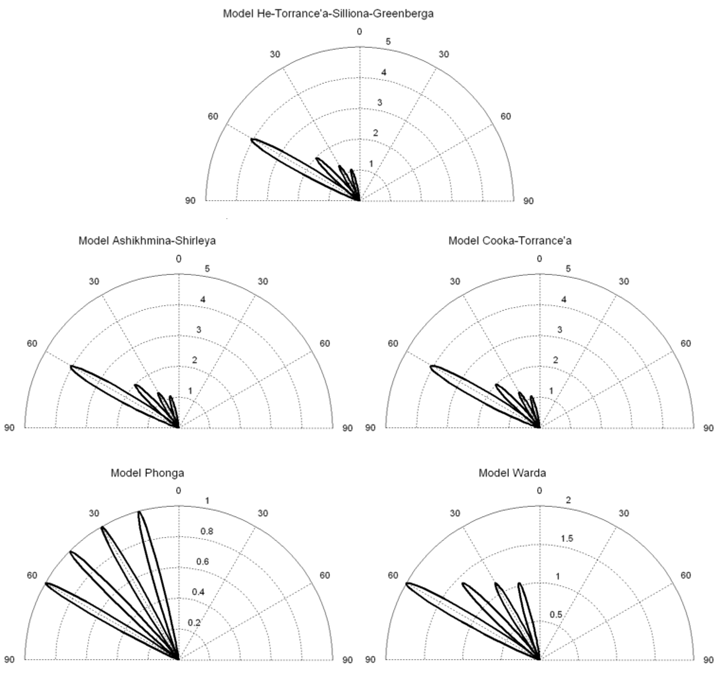
Rys.11.10. Wykresy znormalizowanej funkcji BRDF różnych modeli  dla kątów padania światła :  15^o,  30^o,  45^o,  60^o

Jak widać modele Cooka-Torrance’a, Ashikhmina-Shirleya, He-Torrance’a-Silliona-Greenberga i Warda wykazują zbliżone kształty funkcji BRDF dla różnych kątów padania światła. Przy czym zależności Warda dają inne proporcje zależności kątowych. Model ten nie uwzględnia współczynnika Fresnela. Stąd wartości maksymalne w opisie Warda odbiegają od wartości w modelach Cooka-Torrance’a, Ashikhmina-Shirleya, He-Torrance’a-Silliona-Greenberga.

Jako punkt odniesienia przyjmuje się model He-Torrance’a-Silliona-Greenberga. Badania doświadczalne pokazały, że najlepiej opisuje on zachowanie rzeczywistych powierzchni. Niemniej jednak, ze względu na złożoność obliczeniową i jednocześnie bardzo zbliżone właściwości (rys.11.10) modele Cooka-Torrance’a oraz Ashikhmina-Shirleya są atrakcyjniejsze. Warto pamiętać jednocześnie, że model He-Torrance’a-Silliona-Greenberga nie może być stosowany w odmianach metody śledzenia promieni, gdzie wymagana jest funkcja gęstości prawdopodobieństwa.

Model Phonga nie pasuje do pozostałych, gdyż w ogóle nie uwzględniono w nim ani kąta padania, ani współczynnika Fresnela.