Podręcznik Grafika komputerowa i wizualizacja
Rozdział 6. MODELOWANIE OBIEKTÓW
6.3. Konstruktywna geometria brył
Konstruktywna geometria brył (ang. constructive solid geometry – CSG) jest metodą reprezentacji obiektów polegająca na definicji obiektu jako wyniku regularyzowanych operacji boolowskich (rys. 6.2). Obiekt jest zapisywany (pamiętany) jako drzewo o odpowiedniej budowie ( z określonymi operacjami w węzłach i prymitywami w liściach.
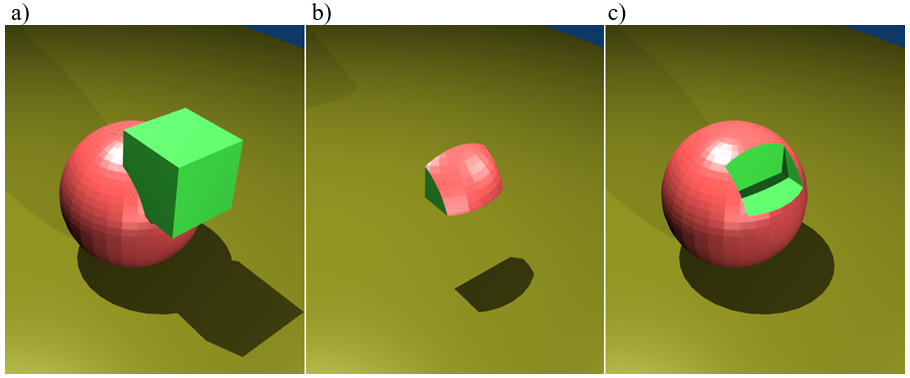
Rys.6.2. a) Suma obiektów, b) iloczyn (część wspólna), c) różnica.
Aby zdefiniować obiekt trzeba podać, z jakich elementów go zbudować (z jakich prymitywów jest on skonstruowany) oraz podać w jaki sposób prymitywy te konstruują obiekt (podać drzewo operacji koniecznych do uzyskania obiektu) – rys.6.3. Najczęściej stosowane operacje to suma, iloczyn (przecięcie), różnica zbiorów.
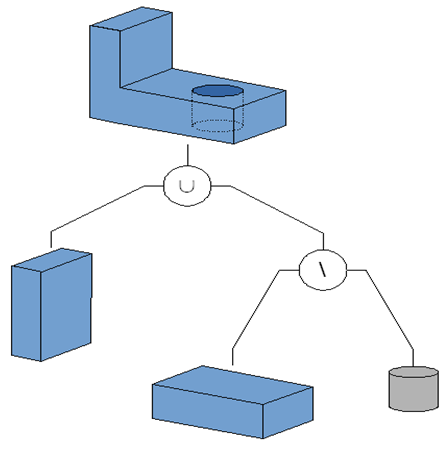
Rys.6.3. Drzewo konstrukcji prostego elementu mechanicznego. Rysunki na podstawie [1].
Zbiór prymitywów:
- Zestaw „klocków” dobranych dla danej sceny, obiektu.
- Prymitywy mogą być definiowane w sposób bardzo ogólny. Np. jako dowolna półprzestrzeń — zbiór punktów (xP, yP, zP) takich że f (xP, yP, zP) < 0, przy czym f jest funkcją ciągłą.
Zestaw prymitywów należy rozumieć bardzo szeroko. Z jednej strony jest to zestaw „klocków” potrzebny do definicji danego zestawu elementów na scenie. Z drugiej strony zestaw ten powinien być na tyle szeroki aby nie stwarzać problemów przy definicji dowolnych elementów sceny w ramach pewnej klasy. Można na przykład założyć że scena będzie zawierała tylko elementy wielościenne. Wtedy naturalnym byłoby zestawienie zbioru prymitywów w postaci wzorców każdego rozpatrywanego typu wielościanu.
Można się zastanowić, czy wygodniejszym nie byłoby użycie tylko jednego prymitywu – półprzestrzeni. W takiej sytuacji za pomocą różnych ustawień półprzestrzeni i operacji boolowskich (regularyzowanych) można byłoby skonstruować dowolny wielościan bez żadnych ograniczeń i co ważne, zawsze w taki sam sposób. Jednak w takiej sytuacji należałoby pamiętać o tym, że w przeciwieństwie do operacji na klockach będących bryłami, operacje przeprowadzane na półprzestrzeniach mogą w ogóle nie dawać bryły. I regularyzacja operacji w takiej sytuacji nie pomoże. Wybór prymitywów jest sprawą bardzo ważną . Powinien być dokonany w zależności od typu obiektów jakie pojawiają się na scenie oraz możliwości systemu modelowania i celów dla jakich został on zbudowany..
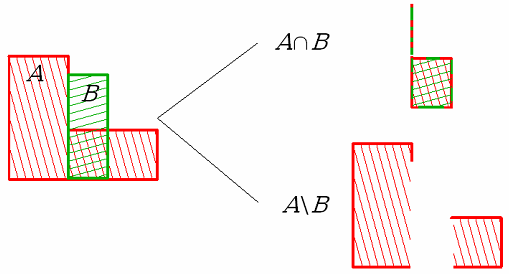
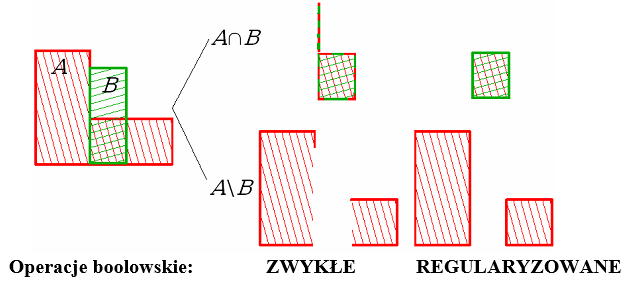
Rys.6.5. Rozwiązanie problemu brzegu (niejednorodności topologicznej) za pomocą regularyzacji operacji.
Konstruktywna geometria brył jest techniką, w której poważnym problemem jest definicja brzegu i wyznaczenie go po wykonaniu operacji boolowskich. Z punktu widzenia obserwatora brzeg jest tym, co świadczy o kształcie obiektu. Patrząc na obiekt widzimy brzeg obiektu (powierzchnię zewnętrzną) i jego właściwości. I na tej podstawie wyrabiamy sobie opinię o obiekcie. W tym kontekście rysowanie brzegu obiektu nie może być związane z jakimikolwiek niejednoznacznościami (rys.6.4). Konsekwentne stosowania operacji regularyzowanych może rozwiązać tego typu problemy (rys.6.5).. Jeśli wykonamy iloczyn lub różnicę brył A i B, to mogą pojawić się obszary dla których nie będzie zdefiniowany brzeg, ale również obszary dla których brzeg będzie określony niejednoznacznie. Zastosowanie regularyzacji zbioru (regularyzowanych operatorów boolowskich) zapewnia poprawność konstrukcji.
Podstawowe właściwości konstruktywnej geometrii brył można scharakteryzować w sposób następujący.
- Zalety
- Bezpośrednia reprezentacja (punkty) w oparciu o operacje boolowskie.
- Reprezentacja zwięzła i efektywna.
- Szczególnie użyteczna w zastosowaniach śledzenia promieni (ray-tracing).
-
Wady
- Aproksymacja obiektu 3D (zależnie od opisu CSG).
- Wizualizacja (czasem) utrudniona (wymaga opisu właściwości powierzchni brzegowej).
- Problem regularyzacji (nietrywialny).
