Podręcznik Grafika komputerowa i wizualizacja

Reprezentacja brzegowa (ang. b-rep – boundary representation) opisuje obiekt za pośrednictwem opisu jego brzegu – powierzchni ograniczającej obiekt (rys.6.6). Możemy tu  mieć do czynienia z modelem wielościennym (ang. polygonal representation) lub powierzchniowym, w którym kształt brzegu obiektu jest opisany parametrycznie.

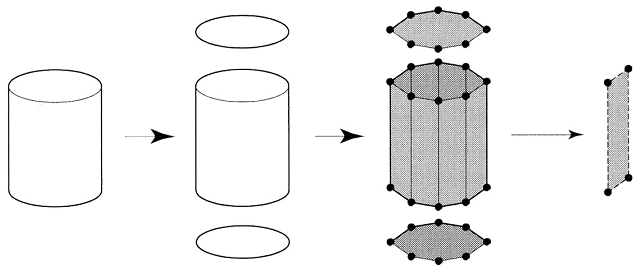
Rys.6.6. Bryła modelowana jako zbiór powierzchni formujących jej brzeg. 
Bryła  =>  Powierzchnie  =>  Wielokąty  =>  Węzły (Krawędzie).

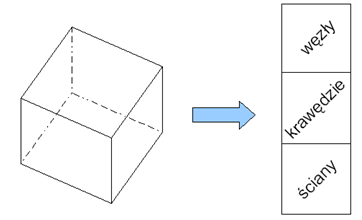
Rys.6.7. Bryła reprezentowana przez jej powierzchnię brzegową.
Dla wielościanu struktura danych pozwala zapamiętać listy (lub tablice)  węzłów, krawędzi i ścian.

Dla modelu wielościennego istotnym problemem jest organizacja struktury danych zapamiętującej obiekt. Realizowane jest to w postaci list lub tablic ścian, krawędzi i wierzchołków. Pamiętanie powiązań między elementami obiektów prowadzi do struktur redundantnych. Wiąże się to oczywiście ze wzrostem kosztu pamięciowego. Czasami celowo wprowadzane są struktury redundantne w celu przyspieszenia wyszukania elementów. Takimi strukturami są na przykład DCEL (double connected edg list) i struktura krawędziowa Baumgarta. Są to struktury, w których deskryptory krawędzi zawierają wskazania na sąsiednie krawędzie, węzły i ściany (rys.6.8).

          

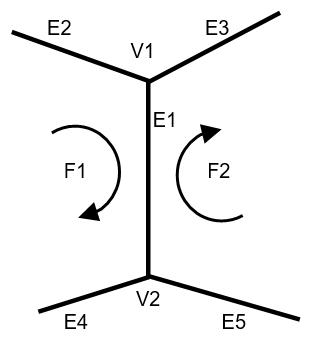
Rys.6.8. „Skrzydlata gałąź” Baumgarta (zaproponowana w 1972).

 Zastosowanie tego typu struktur danych ułatwia wyszukiwanie określonych ciągów elementów. Np. korzystając ze skrzydlatej gałęzi Baumgarta można szybko wyznaczyć pętlę krawędzi dla ściany, albo pętlę krawędzi dla wierzchołka.

 Model wielościenny może być reprezentowany dowolną siatką wielokątów. Rodzaj siatki zależy od budowy obiektu i sposobu jego definiowania. Przypisanie położenia poszczególnym punktom i powiązań tworzących siatkę może być realizowane ręcznie przez konstruktora. Może wynikać z matematycznego opisu obiektu – można wykorzystać charakterystyczne przekroje obiektu, albo linie stałego parametru. Może to być zrealizowane automatycznie na podstawie pomiarów położenia i kształtu obiektu rzeczywistego lub jego modelu. Często wykorzystywane są siatki trójkątów, gdyż przy dowolnym rozmieszczeniu węzłów siatka taka gwarantuje, że każde jej oczko zawsze będzie figurą płaską – wielokątem.

 Problemem na który często jest zwracana uwaga jest trudna weryfikacja poprawności struktury B-rep

 

Wyróżnia się wielościan zwykły (prosta bryła Eulera) dla którego :

Reguła Eulera

                w-k+s=2                        

gdzie:

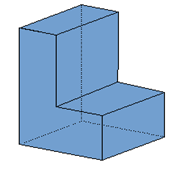
                                                                                                                  w=12. k=18, s=8

Uogólniona reguła Eulera

                w-k+s=2 ^. (c-t)+d

gdzie:

      c — liczba rozłącznych  elementów składowych,
      t — liczba tuneli (w bryle),
      d — liczba dziur (w ścianach)

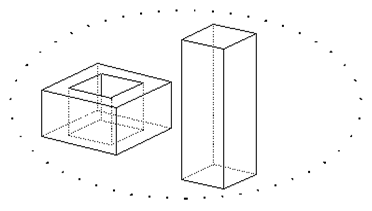
     w=24, k=36, s=16,  c=2, t=1, d=2

 Rys.6.9.Reguła Eulera i uogólniona reguła Eulera.

Dla każdego wielościanu zwykłego spełniona jest reguła Eulera. Rozszerzoną klasę obiektów - rozmaitości dwuwymiarowych obowiązuje uogólniona (rozszerzona) reguła Eulera (rys.6.9).

Należy jednak pamiętać że spełnienie tych warunków jest warunkiem koniecznym ale niewystarczającym przynależności do odpowiedniej klasy. Na przykład sześcian, do którego krawędzi doczepiono prostokąt nie jest już wielościanem zwykłym ale regułę Eulera (podstawową) spełnia.

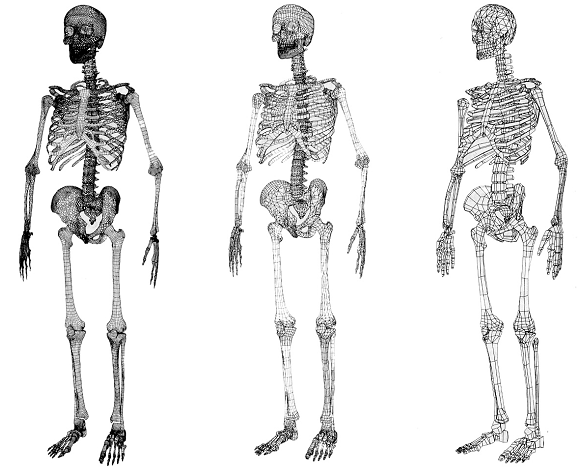
141788 wielokątów       35305 wielokątów      8993 wielokąty

Rys.6.10. Problem aproksymacji kształtu przy modelu wielościennym.
Rysunek pochodzi  z Viewpoint Digital’s catalogue.

Reprezentacja brzegowa jest bardzo efektywna dla obiektów (brył) wielościennych. Dla innych wymagana jest aproksymacja kształtu (np. dla obiektów typu kula czy obiekty obrotowe. Jeśli chcemy oddać kształt obiektu w sposób satysfakcjonujący, to wymagana jest duża liczba wielokątów (rys.6.10). Przy źle zaprojektowanej reprezentacji właściwości modelu wielościennego (i aproksymacji kształtu) mogą prowadzić do utraty cech wizualnych obiektu. 
Reprezentacja brzegowa jest często łączona w systemach modelowania z konstruktywną geometrią brył.

 Podsumowując, właściwości reprezentacji brzegowej można scharakteryzować w następujący sposób