Podręcznik Grafika komputerowa i wizualizacja

Wydawać by się mogło, że najprostszą forma modelowania krzywej jest wskazanie zbioru punktów na niej leżących a następnie połączenie ich krzywą interpolującą – najprościej wielomianową.

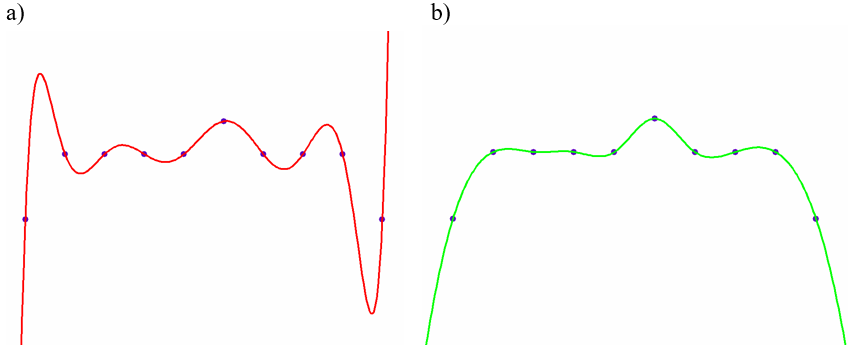
Rys.7.1. Próba modelowania kształtu z wykorzystaniem interpolacji.
a) Krzywą wielomianową stopnia 9.  b) Krzywymi sklejanymi stopnia 3.

Jeżeli dany jest ciąg parami różnych liczb t₀, t₁, t₂, …t_n – węzłów interpolacyjnych i odpowiadających im punktów P₀, P₁, P₂,…P_n. To poszukujemy krzywej wielomianowej P(t) takiej, że jest ona stopnia co najwyżej n oraz  P(t_i)=Pi dla każdego i. Tak sformułowane zadanie jest zadaniem interpolacyjnym Lagrange’a i ma dokładnie jedno rozwiązanie w postaci:

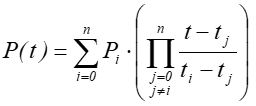
Dla małej liczby punktów (kilku) uzyskana krzywa zachowuje się zgodnie z oczekiwaniem. Niestety dla większej liczby punktów – krzywa wykazuje bardzo dużą wrażliwość na zaburzenia węzłów i skłonność do oscylacji – co pokazuje rysunek 7.1 a). Dodatkowo każdy fragment krzywej zależy od położenia wszystkich węzłów – brak jest lokalnej reprezentacji. Problem oscylacji można rozwiązać korzystając z interpolacji krzywą sklejaną – przedziałami wielomianową niskiego stopnia, rysunek b). Jednak w obu przypadkach kontrola kształtu krzywej pomiędzy węzłami jest trudna.

Wady te powodują, że takie rozwiązanie jest praktycznie nieprzydatne.