Podręcznik Grafika komputerowa i wizualizacja: 8.5. Modelowanie wolumetryczne

Rozdział 8. MODELOWANIE OBIEKTÓW NATURALNYCH. MODELOWANIE FRAKTALNE I WOLUMETRYCZNE

8.5. Modelowanie wolumetryczne

Modelowanie wolumetryczne jest próbą rozwiązania problemu modelowania i wizualizacji zjawisk, które nie dają się opisać w prosty sposób klasycznymi metodami, a które to zjawiska związane są z objętościowym rozproszeniem światła. Efekt taki powstaje zazwyczaj na skutek istnienia pewnego dodatkowego czynnika zmieniającego warunki rozchodzenia się światła. Przykładem może być mgła, chmury lub wydobywający się gaz.

Podobne efekty mogą powstawać przy przechodzeniu światła przez niejednorodne ośrodki półprzezroczyste np. powierzchnię morza.

Wykorzystując modelowanie wolumetryczne modeluje się przekroje na potrzeby prześwietleń w medycynie. Są to wizualizacje trójwymiarowego pola skalarnego. Dane uzyskane ze skanowania obiektów w tomografii komputerowej (Computer Tomography - CT), rezonansie magnetycznym (Magnetic Resistance Imaging - MRI), tomografii pozytronowej (Positron Emission Tomography - PET). Najczęściej jest to związane z wizualizacją trójwymiarowej funkcji pochłaniania promieniowania. Funkcja ta określona jest dla każdego punktu przestrzeni pokazując właściwości badanej tkanki. W symulacjach naukowych również często stosuje się wizualizacje pola trójwymiarowego wykorzystując dane z modeli matematycznych lub informacje uzyskane z przeprowadzonych eksperymentów.

Rys.8.14. Przykład modelowania wolumetrycznego. Nocne szachy i nocne szachy z mgiełką.
Rysunki Łukasz Stelmach ©, POV-Ray. Rysunki publikowane za zgodą Autora.

Wizualizacja zjawisk naturalnych jako pola skalarnego może obejmować naturalne zjawiska atmosferyczne takie jak np. mgła, deszcz, chmury. Zjawiska gazowe takie jak np. turbulencje powietrza, para, płomień.

Najczęściej w grafice komputerowej stosuje się następujące metody:

Metody uproszczone. Wizualizacja za pomocą tekstur (dwuwymiarowych rzadziej trójwymiarowych). Wizualizacja za pomocą półprzepuszczalnych płaszczyzn (jednej lub kilku) z nałożonymi obrazami zjawiska. Metody te dają dobre efekty i są efektywnie obliczeniowo, ale związane są tylko z określonym kierunkiem patrzenia. Metody takie stosuje się do uproszczonego modelowania mgły i chmur oraz podobnych zjawisk (np. w grach komputerowych).
Metoda próbek w przestrzeni (particle tracing) polegająca na umieszczeniu (zazwyczaj półprzezroczystych) elementów (kul, walców, sześcianów) w przestrzeni, mających rozpraszać światło – lub generalnie zmieniać warunki jego rozchodzenia się. Metodami takimi wizualizuje się chmury, mgłę i podobne zjawiska.
Metoda analizy objętościowej. (volume rendering) polegająca na przypisaniu właściwości rozpraszających określonym punktom w przestrzeni. Jest to realizowane najczęściej w postaci wokselowej – każdy weksel ma określone parametry związane z przechodzeniem światła. Podczas śledzenia promieni wyznaczane są woksele na drodze promienia i ich parametry wpływają na barwę promienia. Analogicznie jest analizowane tak zwane światło wolumetryczne (volume light). Metody te stosuje się przede wszystkim w medycynie. Czasami stosuje się je do modelowania mgły lub chmur. Światło wolumetryczne pozwala symulować reflektory świecące we mgle, kurz unoszący się w powietrzu i rozpraszający światło w delikatny sposób, zadymione pomieszczenia.
Metody uproszczonego opisu fizycznego zjawiska. Opis szumu trójwymiarowego i turbulencji, wykorzystanie szumu Perlina. Takie metody najczęściej stosuje się do wizualizacji płomienia, dymu, chmur, tworzenia efektu ognia i wybuchu. Metody te są często realizowane w postaci złożonej tekstury trójwymiarowej.

Aby uprościć zadanie modelowania wolumetrycznego stosuje się podział przestrzeni na komórki elementarne. Najczęściej wymaga się od komórek, aby były one wypukłe, minimalne (elementarne) na tyle, na ile pozwalają zobrazować oczekiwane szczegóły, niezależne w ramach podziału przestrzeni.

W zależności od celu wizualizacji, obiektu (pola skalarnego) oraz przyjętego uproszczenia można stosować różne rodzaje komórek:

Sześcienne (woksele odpowiadające podziałowi równomiernemu w układzie współrzędnych).
Regularne (prostopadłościenne).
Regularne o zmiennych rozmiarach.
„Strukturalne” (proste wielościany).
„Niestrukturalne” (skomplikowane wielościany, piramidy).
Hybrydowe (kombinacje powyższych).

Dobrym przykładem modelowania wolumetrycznego wykorzystującego najprostszy podział przestrzeni jest modelowanie chmur (rys.8.15). W zależności od kształtu chmury jej gęstości i barwy, wybierane są odpowiednie komórki przestrzeni, w których „znajduje się” chmura. Następnie przeprowadzane jest wygładzanie sąsiednich komórek w przestrzeni. Ostatni etap to wizualizacja z uwzględnieniem lokalnych zmian barwy komórek oraz przezroczystości. Przedstawiony sposób jest rzeczywiście jednym z najprostszych metod rysowania chmur, jednak dającym dość dobre rezultaty. Istnieje wiele innych metod uwzględniających także właściwości fizyczne takie jak pochłanianie czy załamanie światła. Odpowiednie opisy można znaleźć w literaturze.

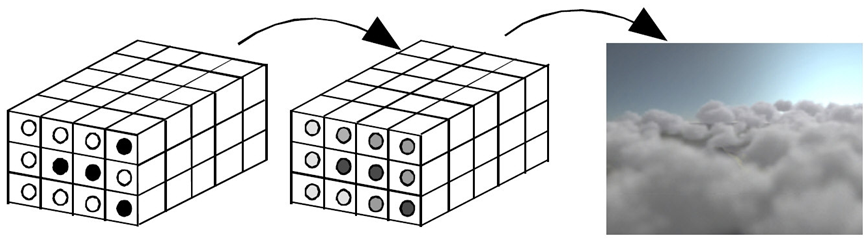
Rys.8.15. Przykład wolumetrycznego modelowania chmur.
Rysunki na podstawie: Dobashi Y.: A Simple, Efficient Method for Realistic Animation of Clouds, SIGGRAPH’00.

Przykładem podejścia „warstwowego” w modelowaniu wolumetrycznym może być modelowanie płomienia (rys.8.16). Prezentowana metoda wykorzystuje dodatkowe techniki dając bardzo efektywne rozwiązanie. Płomień jest w tej metodzie modelowany następującymi etapami:

Przestrzeń obejmującą płomień jest dzielona na warstwy.
W każdej warstwie generowana jest tekstura na podstawie bardzo prostego modelu zmian temperatury (i barwy).
Tekstura jest zaburzana funkcją turbulencji.

Rys.8.16. Przykład warstwowego modelowania płomienia. Na podstawie [5].

Podział na warstwy musi uwzględniać rozdzielczość tekstury – płomień nie zawsze będzie obserwowany z kierunku dokładnie prostopadłego do tekstury warstwy. Jednocześnie funkcja turbulencji powinna uwzględniać zjawiska fizyczne nie tylko w płaszczyźnie warstwy ale także między nimi. Proste podobieństwo między sąsiednimi warstwami nie rozwiązuje sprawy, gdyż może prowadzić do nienaturalnego wyglądu obiektu szczególnie przy zmianie kąta patrzenia. Biorąc pod uwagę modelowanie płomienia dla potrzeb animacji warto zauważyć także pewne reguły zmian obiektu występujące między kolejnymi klatkami (rys.8.17). Kolejne warstwy płomienia w ramach jednej klatki zmieniają się zgodnie z omówionymi wcześniej zasadami. Natomiast ta sam warstwa w kolejnych klatkach animacji powinna wyglądać tak samo (lub podobnie) ale z uwzględnieniem wrażenia unoszenia się płomienia do góry.

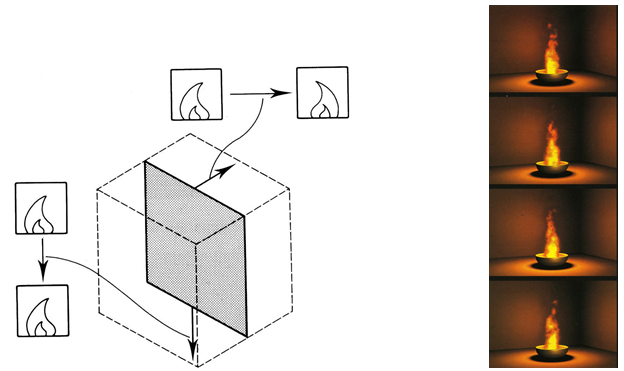
Rys.8.17. Modelowanie kolejnych klatek animacji płomienia. Na podstawie [5].

Modelowanie wolumetryczne wykorzystuje wiele różnych metod, czasami dość zaskakująco łączonych ze sobą. Często stosowane są techniki teksturowania oraz funkcje wprowadzające lokalne zaburzenia lub szum. Warto zwrócić uwagę na funkcję szumu opracowaną przez K.Perlina w 1985 roku (uzupełnioną w 2002). Funkcja ta jest gładką interpolacją wektora gradientu między węzłami siatki. Jest ona prosta w implementacji i daje zaskakująco dobre efekty. Z tego powodu szum Perlina jest często dodawany do tekstur różnych powierzchni, aby podkreślić drobne niejednorodności rzeczywistych obiektów i nadać im naturalny wygląd.