Podręcznik Grafika komputerowa i wizualizacja

Pomysł wykorzystania zorientowania ścian pochodzący z 1969 roku (Schumacker) został zastosowany w latach 1980-1983 do budowy algorytmu rozstrzygania widoczności zwanego algorytmem drzewa binarnego podziału przestrzeni (ang. BSP tree). Autorami algorytmu są Fuchs, Kedem, Taylor.

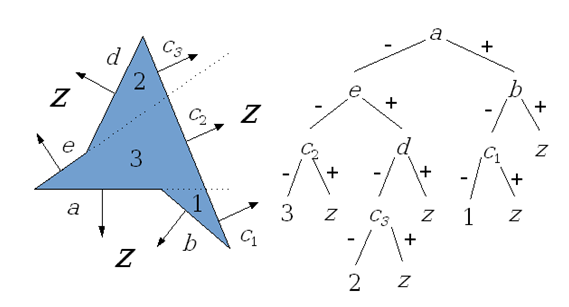
Rys.9.12. Podział przestrzeni płaszczyznami a,b,c,d,e oraz odpowiadające temu podziałowi
drzewo binarne. Strzałki oznaczają zorientowanie dodatnie (+), z – oznacza obszar zewnętrzny.

Rozpatrzmy przypadek jak na rysunku 9.12. Każdej płaszczyźnie można przypisać zorientowanie (zaznaczone strzałkami, zwrot zgodny ze strzałkami w drzewie został zaznaczony + , zwrot przeciwny został oznaczony - ). Kolejność analizy (budowy drzewa podziału) – to znaczy wybór kolejnych płaszczyzn jest dowolny. Może to oczywiście wpłynąć na kształt drzewa, wpływa także na konieczność podziału ścian wielościanu. Na przykład ściana c na rysunku została podzielona na fragmenty c₁, c₂ i c₃ co wynika z wcześniejszego podziału przestrzeni. Algorytm podziału binarnego w takiej postaci może zostać także wykorzystany do sprawdzenia czy dany punkt należy do wnętrza wielościanu.

 

ALGORYTM_PODZIAŁU_BINARNEGO

1. zbuduj drzewo BSP tak, aby każdy obiekt (przynajmniej) znalazł się    w odrębnej komórce.

2. przeglądaj drzewo w kolejności INORDER z uwzględnieniem zorientowania.

    procedure przeglądaj_BSP (drzewo)

    begin

                if drzewo jest niepuste then

                            if  obserwator „z przodu” (+) korzenia drzewa then

                                        begin 

                                                    przeglądaj_BSP (tylne (-) poddrzewo);

                                                   narysuj obiekt z korzenia drzewa;

                                                    przeglądaj_BSP (przednie (+) poddrzewo);

                                        end;

                            else   // tu obserwator „z tyłu” (-) korzenia drzewa

                                        begin 

                                                    przeglądaj_BSP (przednie (+) poddrzewo);

                                                    narysuj obiekt z korzenia drzewa;

                                                    przeglądaj_BSP (tylne (-) poddrzewo);

                                        end;

    end;

 

W warunkach rzeczywistej analizy sceny przy wyborze płaszczyzn podziału warto posługiwać się płaszczyznami związanymi bezpośrednio z obiektami (zawierającymi na przykład ściany). Przykład przekroju sceny i odpowiadające mu drzewo podziału prezentuje rysunek. Zakładamy dla uproszczenia, że w każdym obszarze (ponumerowanym) znajduje się jeden obiekt. Stosując algorytm binarnego podziału należy wyznaczyć kolejność rysowania, w taki sposób, aby z punktu widzenia obserwatora rysować obiekty od najdalszych do najbliższych (najpierw zasłaniane potem zasłaniające). Drzewo uwzględnia wszystkie ściany i pozwala wskazać kolejność zasłaniania po przejściu zaproponowanym algorytmem drzewa.

Oczywiście drzewo nie uwzględnia położenia obserwatora, natomiast położenie to wpływa na drogę przejścia przez drzewo. Rysunek 9.13 pokazuje różne kolejności rysowania obiektów dla dwóch różnych położeń obserwatora.

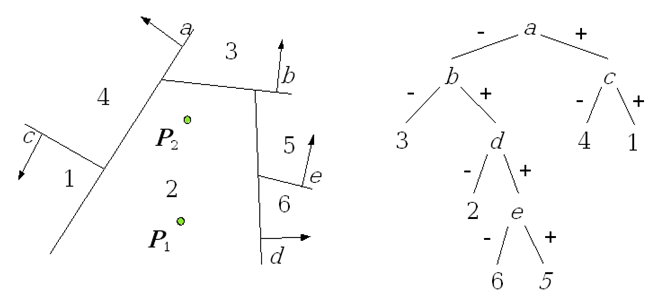
Rys.9.13. Podział przestrzeni i odpowiadające mu drzewo BSP.
Kolejność rysowania obiektów zależna od położenia obserwatora.
Obserwator w P₁ kolejność rysowania: 4,1,3,5,6,2.
Obserwator w P₂ kolejność rysowania: 1,4,3,6,5,2.

Ciekawym przypadkiem jest sytuacja, gdy obserwator znajduje się wewnątrz obszaru. Wtedy drzewo binarnego podziału pokazuje właściwą kolejność bez względu na kierunek patrzenia obserwatora !

Algorytm drzewa binarnego podziału przestrzeni był bardzo długo traktowany jako niezwykle elegancka ciekawostka, ze względu na skomplikowanie tworzenia drzewa podziału. Dopiero silny rozwój gier komputerowych w latach 90 dwudziestego wieku spowodował, że algorytm ten przeżywa swój renesans. Zauważono bowiem, że warto na użytek gier rozdzielić etap tworzenia drzewa od etapu przeglądania. Jeśli przyjmiemy, że w każdym elemencie podziału znajduje się jeden obiekt sceny, to samo przeglądanie algorytmem INORDER  ma złożoność liniową ze względu na liczbę obiektów  i to niezależnie od zbalansowania drzewa.

Drzewo zostaje zatem  utworzone przez twórców gry w momencie generowania „mapy” gry. Natomiast przeglądane jest w momencie realizacji (wirtualnego poruszania się gracza/bohatera po świecie gry). Co więcej, sprawę można dodatkowo uprościć dzieląc mapę na obszary, w których jest ustalona kolejność rysowania obiektów, a następnie zapisać gotowe schematy kolejności dla poszczególnych obszarów. W tym przypadku podczas realizacji gry nawet przeglądanie drzewa nie jest potrzebne.

Warto dodać, że w latach 1992-1995 (prace Tellera, Luebkego, Georgesa) powstała metoda wyboru potencjalnych elementów widocznych (ang.PVS – Potentially Visible Set) pozwalająca określić przybliżony zakres widoczności obiektów. Metoda ta jest często łączona z generacją drzewa BSP.

 

Podstawowe właściwości algorytmu podziału binarnego można scharakteryzować w następujący sposób:

• Zalety:
  • Prosty i elegancki. Niepotrzebna informacja o głębokości.
  • Tylko zapis do bufora rysunku (framebuffer), niepotrzebne porównywanie bieżącego położenia (jak w Z_buforze), ani sortowania (jak w malarskim).
  • Można podzielić na preprocesing (budowanie drzewa) i przeglądanie drzewa (rysowanie) !!!
  • Bardzo szybkie rysowanie – złożoność O(n) , efektywne wykorzystanie w grach komputerowych.
• Wady:
  • Duża złożoność preprocesingu ogranicza zastosowanie do scen statycznych.
  • Konstrukcja drzewa: O(nlogn) podziału i sortowania.
  • Podział powiększa liczbę wielokątów: O(n²) .