Podręcznik: Formalizacja elementów PD

1. Programowanie dynamiczne

1.1. Formalizacja elementów PD

Programowanie dynamiczne wymaga wyróżnienia etapów (ang. stages), w których są podejmowane decyzje (akcje, ang. actions) specyficzne dla konkretnych stanów (ang. states) procesu decyzyjnego. Przejścia (ang. transitions) z jednego stanu do drugiego, wiążą się z kosztem i są efektem podjętej decyzji, lub losowego zdarzenia (deterministyczne vs. stochastyczne PD).

Własność Markowa. Stan (czyli wartość) zmiennych decyzyjnych

$x$ w danym etapie

$t$ zależy tylko od stanu oraz akcji

$u$ z poprzedniego etapu

$t-1$ , zgodnie z funkcją przejścia

$g(\cdot)$ :

$x_{t+1} = g(x_t, u_t),\;\; \forall t = 1\ldots T-1$

Proces decyzyjny spełniający tę własność jest procesem Markowa, który można przedstawić tak jak na poniższym schemacie.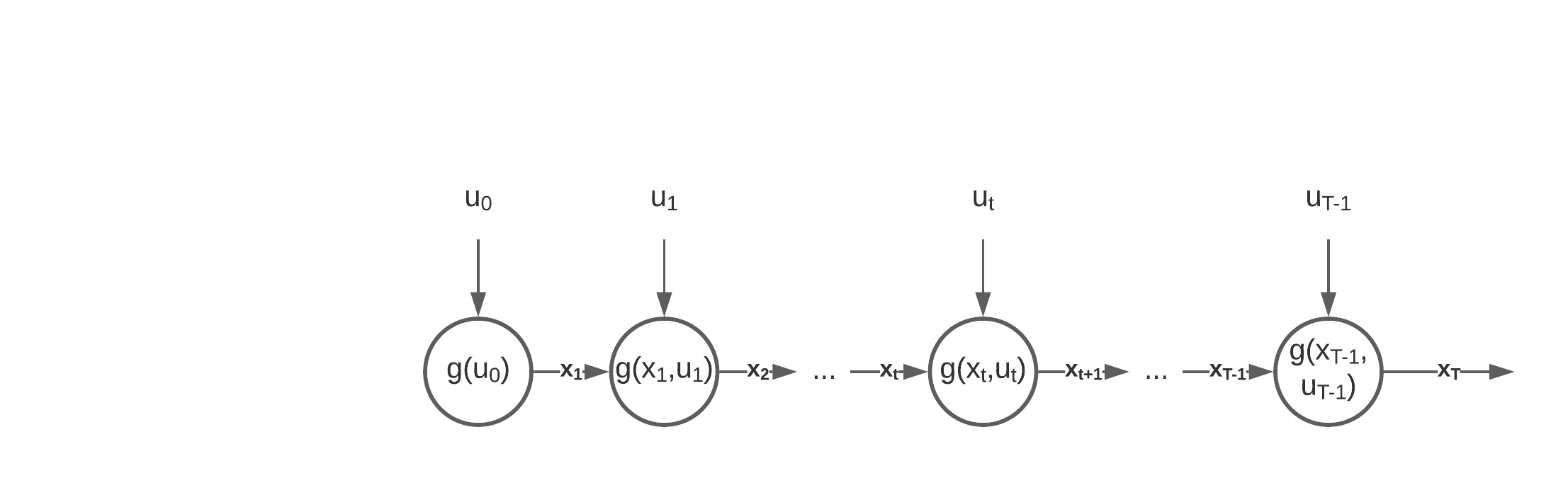 schemat procesu markowa

Zauważmy, że w końcowym etapie T nie podejmujemy decyzji.

Własność Markowa musi być spełniona aby można było zastosować PD. Drugim warunkiem jest możliwość dekompozycji funkcji celu na stany i etapy.

Separowalność funkcji celu. Funkcja celu jest separowalna jeśli można ją zdekomponować na mniejsze funkcje, operujące na zmiennych i parametrach odnoszących się do konkretnych etapów:

$f(u_0, x_1, u_1, x_2\ldots, u_{T-1}, x_T) = H(f_1(x_1,u_0), f_{t+1}(x_{t+1},u_t),\ldots,f_T(x_T,u_{T-1}))$
Najczesciej oznacza to addytywnosc komponentów f. celu. Inna mozliwosc to np. mnożenie, etc..

Podsumowując, dla problemów spełniających powyższe własności definiujemy następujące elementy PD:

Etapy,
Stany – wartości, które mogą przyjmować zmienne decyzyjne w każdym z etapów,
Przejścia z jednego stanu do kolejnego, które są efektem podjętej decyzji,
Funkcja Bellmana (value function), która określa w konkretnym etapie najlepszą wartość funkcji celu, osiągalną z konkretnego stanu.

Funkcja Bellmana. Dla addytywnie separowalnej funkcji celu:

$\min_{x,u} f(u_0, x_1, u_1, x_2\ldots, u_{T-1}, x_T) = \min_{u_0}f_1(x_1,u_0)+ \min_{u_t} f_{t+1}(x_{t+1},u_t),\ldots, \min_{u_{T-1}} f_T(x_T,u_{T-1})$
Optymalne rozwiązanie wyznaczymy szukając decyzji, która oprócz lokalnej funkcji celu uwzględnia wartość w kolejnym etapie.

dla każdego $x_T$ (stan końcowy) przyjmujemy $V_T(x_T)=f(x_T)$ (terminal value function)
do stanu końcowego doprowadza nas decyzja $u_{T-1}$ podjęta w stanie $x_{T-1}$
dla optymalnej decyzji $u_{T-1}$ dojścia ze stanu $x_{T-1}$ do $x_{T}$ wyznaczymy wartość:
$V_{T-1}(x_{T-1})=\min_{u_{T-1}}\left\{ V_T(x_T) + f_{T}(x_{T},u_{T-1})\right\}$
z równania stanu wiemy, że $x_{t+1} = g(x_t, u_t)$ , czyli:
$V_{T-1}(x_{T-1})=\min_{u_{T-1}}\left\{V_T(g(x_{T-1},u_{T-1})) + f_{T}((g(x_{T-1},u_{T-1}),u_{T-1})\right\}$
w ogólnej postaci, rekurencyjne równanie Bellmana zapisujemy jako:
$V_t(x_t) = \min_{u_t} \left\{ V_{t+1}(g(x_t,u_t))+f_{t+1}(g(x_t, u_t),u_t)\right\}$