Podręcznik

Rozwiążemy problem inwestycyjny, definiując poszczególne elementy PD.  

Załóżmy, że inwestor dysponuje budżetem 10 mln zł. Ma do wyboru 8 różnych możliwości, każda z nich charakteryzuje się różną stopą zwrotu, podaną w tabeli. Aby ograniczyć ryzyko nadmiernej koncentracji kapitału inwestor nie chce wydać więcej niż 4 mln zł na pojedynczą opcję. Przyjmuje się, że można zainwestować tylko wielokrotności 1 mln zł. Pozostała, niezainwestowana gotówka daje zwrot w wysokości 5 tys. zł za każdy milion.

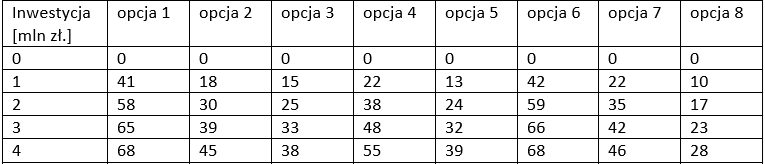
Dla powyższego zadania, które jest odmianą problemu plecakowego definiujemy:

• etapy $t$: opcje inwestycyjne,
• stany $x_t$: zainwestowana gotówka przed rozważeniem opcji $t$,
• sterowanie $u_t$: ile zainwestować gotówki w opcję $t$,
• funkcja przejścia:  $x_{t+1}=x_t+u_t$,
• wartość końcowa w tym zadaniu nie jest zerowa, określa ją zwrot z pozostałej, niezainwestowanej gotówki:  $V_T(x_T)=(10-x_T)\cdot 0.5$,
• funkcja Bellmana odnosi się w tym przypadku tylko do zysku z decyzji:  $V_t(x_t)=\max_{u_t}\{f(u_t)+V_{t+1}(x_t+u_t)\}$.

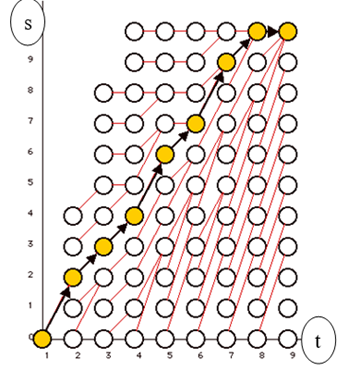
Problem ten można przedstawić w postaci grafu PD, tak jak na poniższej ilustracji, gdzie zaznaczono też optymalne rozwiązanie.