Podręcznik

Sortowanie szybkie, znane powszechnie pod nazwą QuickSort, to jeden z najwydajniejszych i najczęściej stosowanych algorytmów sortujących w praktyce. Został opracowany w 1960 roku przez brytyjskiego informatyka Tony'ego Hoare’a i od tego czasu zdobył ogromną popularność ze względu na swoją szybkość oraz elegancką, rekurencyjną strukturę. Mimo że w najgorszym przypadku jego złożoność czasowa wynosi O(n²), to w większości rzeczywistych zastosowań działa z wydajnością O(n log n), co czyni go bardzo skutecznym wyborem. Podstawową ideą sortowania szybkiego jest technika „dziel i zwyciężaj”. Działanie algorytmu możemy podzielić na następujące etapy:

• Etap dziel - algorytm wybiera specjalny element zwany pivotem (osią podziału), a następnie przekształca tablicę w taki sposób, że wszystkie elementy mniejsze od pivota trafiają na lewo od niego, a większe – na prawo. Dzięki temu pivot znajduje się na swojej właściwej, końcowej pozycji w tablicy, nawet jeśli pozostałe elementy nie są jeszcze uporządkowane.
• Etap zwyciężaj - po podziale na dwie podtablice – lewą i prawą względem pivota – każda z nich jest sortowana niezależnie. Etap ten przebiega rekurencyjnie: algorytm stosuje dokładnie ten sam schemat (czyli „dziel i zwyciężaj”) dla obu części aż do momentu, gdy tablice zawierają po jednym lub żadnym elemencie, co oznacza, że są już z natury posortowane.
• Etap połącz - w algorytmie QuickSort ma charakter niejawny. W przeciwieństwie do innych algorytmów opartych na tej samej strategii, takich jak sortowanie przez scalanie, QuickSort nie wymaga dodatkowego etapu łączenia. Dzięki temu, że wszystkie zamiany elementów dokonywane są bezpośrednio w tablicy T, po zakończeniu wszystkich rekurencyjnych wywołań otrzymujemy posortowaną wersję tej samej tablicy. Nie zachodzi potrzeba kopiowania danych czy tworzenia pomocniczych struktur – posortowany wynik jest po prostu efektem końcowym operacji wykonanych w miejscu.

W pierwszej kolejności pokażemy wybór środkowego elementu tablicy jako elementu rozdzielającego oraz podział na partycje

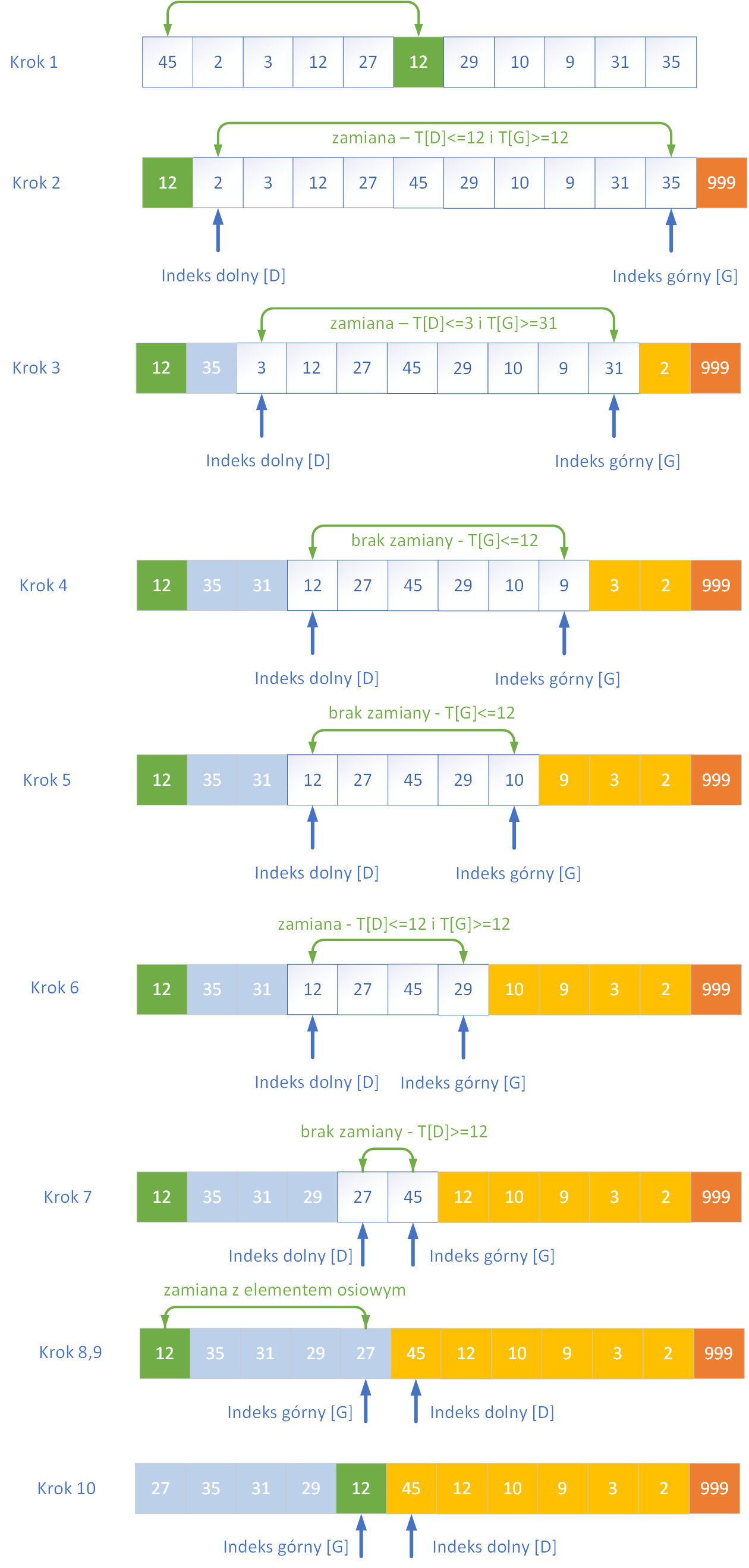
Działanie podziału przebiega według następującego schematu:

1. Wybierz element środkowy tablicy i zamień go z pierwszym elementem – stanie się on elementem osiowym (pivotem). 
2. Ustaw wskaźnik dolny na pozycji T[1], a wskaźnik górny na pozycji T[n–1].
3. W ostatniej komórce T[n] umieść wartownika – bardzo dużą wartość większą od wszystkich pozostałych elementów tablicy. 
4. Rozpocznij przesuwanie wskaźników: 
   • dolny[D] przesuwa się w prawo, górny[G] – w lewo. 
   • wskaźnik dolny[D] zatrzymuje się, gdy napotka element większy lub równy pivotowi. 
   • wskaźnik górny[G] zatrzymuje się, gdy natrafi na element mniejszy lub równy pivotowi. 
   • jeśli wskaźniki się nie minęły, zamień miejscami elementy wskazywane przez dolny i górny wskaźnik. 
5. Powtarzaj kroki do momentu, aż wskaźniki się miną (czyli dolny > górny). Gdy wskaźniki się miną, zamień element osiowy (T[0]) z elementem wskazywanym przez wskaźnik górny (T[G]). Element osiowy znajduje się teraz we właściwym miejscu, a tablica jest podzielona na dwie części gotowe do dalszego sortowania.

Po zakończeniu podziału tablicy względem elementu osiowego (pivotu), algorytm kontynuuje działanie w dwóch niezależnych częściach. QuickSort wywoływany jest rekurencyjnie dla lewej oraz prawej podtablicy powstałych po podziale. W każdej z nich ponownie wybierany jest nowy pivot i przeprowadzany jest lokalny podział. Proces ten powtarza się aż do momentu, gdy każda podtablica będzie zawierać co najwyżej jeden element – wówczas dalsze sortowanie nie jest już potrzebne. W ten sposób cała tablica zostaje posortowana, bez potrzeby dodatkowego scalania fragmentów. Poniżej przedsatwiono przykładowy kod realzujący sortowanie szybkie.

#include <iostream>
#include <vector>
using namespace std;

// Funkcja pomocnicza do zamiany elementów
void swap(int& a, int& b) {
    int temp = a;
    a = b;
    b = temp;
}

// Funkcja dzieląca tablicę – wybór pivota i podział
int partition(vector<int>& T, int left, int right) {
    int pivot = T[right]; // wybór elementu osiowego (pivot)
    int i = left - 1;

    for (int j = left; j < right; j++) {
        if (T[j] < pivot) {
            i++;
            swap(T[i], T[j]);
        }
    }

    swap(T[i + 1], T[right]); // pivot na właściwym miejscu
    return i + 1;
}

// Rekurencyjna funkcja sortująca
void quickSort(vector<int>& T, int left, int right) {
    if (left < right) {
        int pivotIndex = partition(T, left, right); // podział tablicy na partycje

        // Rekurencyjne wywołania sortujące lewą i prawą część
        quickSort(T, left, pivotIndex - 1);
        quickSort(T, pivotIndex + 1, right);
    }
}

// Pomocnicza funkcja do wypisania tablicy
void printArray(const vector<int>& T) {
    for (int x : T) {
        cout << x << " ";
    }
    cout << endl;
}

// Przykład użycia
int main() {
    vector<int> T = { 9, 3, 7, 1, 5, 8, 2, 6, 4 };

    cout << "Przed sortowaniem: ";
    printArray(T);

    quickSort(T, 0, T.size() - 1);

    cout << "Po sortowaniu: ";
    printArray(T);

    return 0;
}