Podręcznik

Sortowanie kubełkowe (ang. Bucket Sort) to algorytm sortujący, który opiera się na założeniu, że dane wejściowe są równomiernie rozłożone na pewnym przedziale wartości. Zamiast porównywać elementy między sobą, jak w klasycznych metodach sortowania, algorytm ten dzieli dane na grupy zwane kubełkami (ang. buckets), a następnie sortuje każdy kubełek osobno i łączy ich zawartość w jeden uporządkowany ciąg. Działanie algorytmu rozpoczyna się od podzielenia przestrzeni możliwych wartości na określoną liczbę przedziałów. Każdy z tych przedziałów reprezentuje osobny kubełek, do którego trafiają elementy spełniające odpowiedni warunek – na przykład wartości mieszczące się w danym zakresie. Po przydzieleniu wszystkich elementów do odpowiednich kubełków, każdy z nich jest sortowany osobno, zwykle za pomocą prostych metod, takich jak sortowanie przez wstawianie. Na koniec zawartość kubełków jest scalana w jedną uporządkowaną tablicę. Algorytm ten najlepiej sprawdza się w przypadku danych rzeczywistych (np. liczb zmiennoprzecinkowych z przedziału [0, 1)), których rozkład jest stosunkowo równomierny. W idealnych warunkach, gdy dane rozkładają się równomiernie, sortowanie kubełkowe może osiągnąć złożoność czasową O. Jednak w mniej korzystnych przypadkach – na przykład gdy wszystkie dane trafią do jednego kubełka – wydajność może spaść nawet do O(n²), jeśli wewnątrz kubełków użyjemy sortowania elementarnego.
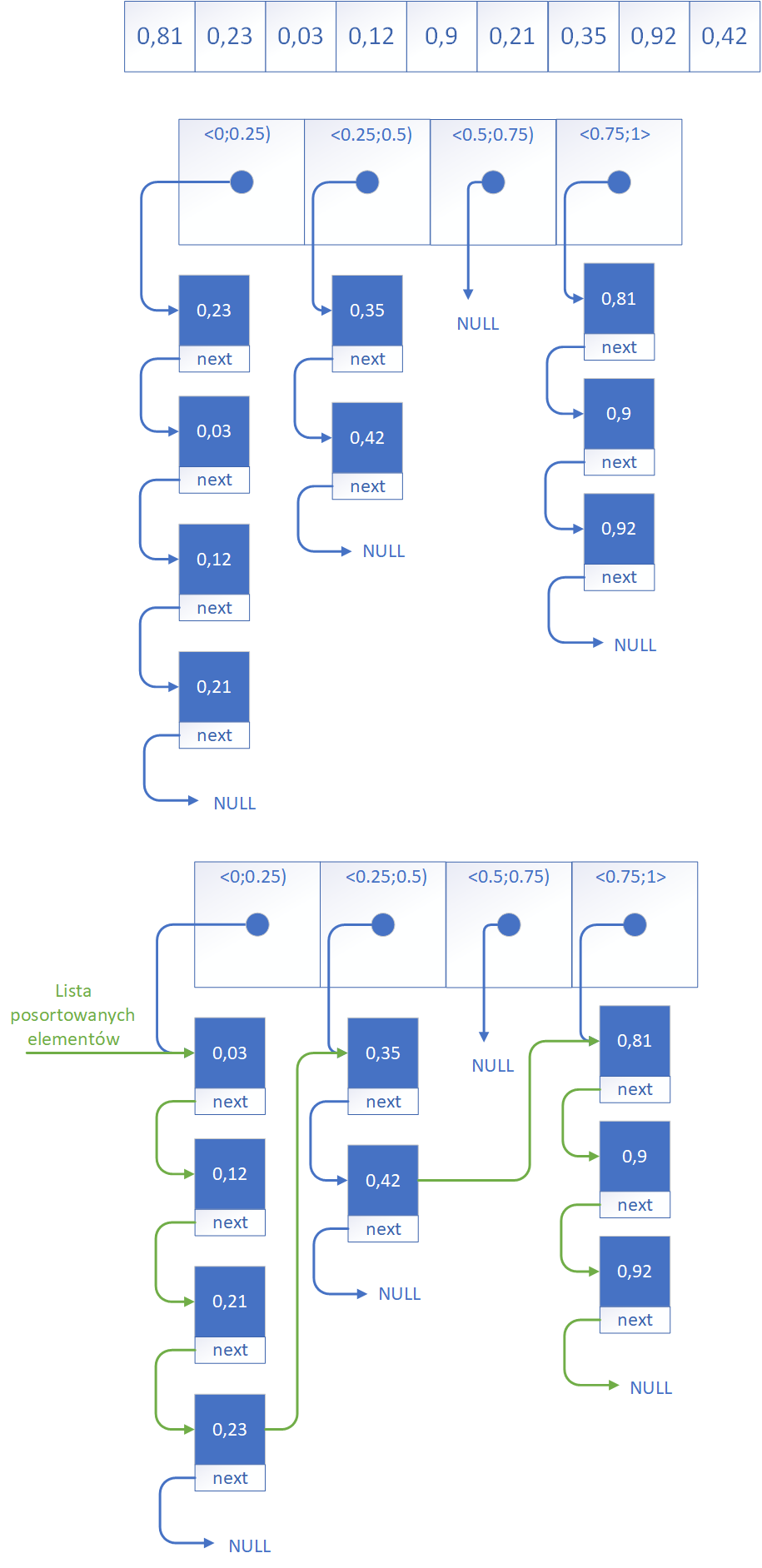
Poniżej na rysunku zostanie przedstawiony przykład działania sortowania kubełkowego dla tablicy liczb rzeczywistych z przedziału <0;1>. Zdecydowano się podzielić zakres na następujące podprzedziały oznaczające kubełki: <0;0.25), <0.25;0.5), <0.5;0.75), <0.75;1>.

Działanie algorytmu możemy prześledzić na przykładzie rysunkowym. Składa się z następujących etapów:

• Podział przedziału liczbowego na m równych części (kubełków) - na samym początku algorytm określa zakres wartości, w którym mieszczą się wszystkie dane wejściowe. Jest to wymagane aby nie pominąć żadnej wartości. Zakres jest następnie dzielony na m równych podprzedziałów. Każdy z tych podprzedziałów stanowi osobny kubełek (ang. bucket), do którego trafią elementy należące do danego fragmentu zakresu. Wybór liczby kubełków oraz sposobu podziału zależy od charakteru danych i ma wpływ na efektywność sortowania.
• Przenoszenie elementów do odpowiednich kubełków - następnie każdy element ze zbioru danych jest analizowany pod względem swojej wartości i umieszczany w odpowiednim kubełku. W podprzedziale, do którego należy. Na przykład liczba 0,34 trafi do kubełka obejmującego przedział <0.25; 0.5). Proces ten przypomina klasyfikowanie elementów według ich przybliżonego położenia w uporządkowanej tablicy. Każdy kubełek zawiera wskaźnik na początek listy w której znajdują się wartości do niego należące.
• Sortowanie elementów wewnątrz każdego kubełka - po dokonaniu podziału danych do kubełków, każdy z nich może zawierać kilka elementów, które należy jeszcze uporządkować. Wewnątrz każdego kubełka stosuje się zazwyczaj prosty i szybki algorytm sortujący, taki jak sortowanie przez wstawianie (ang. Insertion Sort), ponieważ liczba elementów w pojedynczym kubełku jest zwykle niewielka. Ten krok zapewnia, że każdy kubełek będzie lokalnie posortowany.
• Scalanie zawartości kubełków w jedną strukturę wynikową - ostatni krok polega na połączeniu wszystkich posortowanych kubełków w jednej strukturze wynikowej. Kubełki są scalane w kolejności odpowiadającej ich zakresom, czyli od najmniejszego do największego. Dzięki temu, że każdy kubełek zawiera elementy z określonego fragmentu całego zakresu, a jego zawartość została wcześniej uporządkowana, scalona tablica jest już w pełni posortowana. Nie ma potrzeby wykonywania dodatkowego sortowania po złączeniu zawartości kubełków. Należy połączyć wszystkie listy w jedną posortowaną listę wartości.