Podręcznik
Wymagania zaliczenia
Wersja podręcznika: 1.0
Data publikacji: 01.01.2022 r.
5. Sterty i sortowanie kopcowe
Sterta (ang. heap) to specjalna struktura danych w postaci drzewa binarnego, która spełnia warunek porządku kopca. Oznacza to, że w kopcu maksymalnym (ang. max-heap) każdy rodzic ma wartość większą lub równą swoim dzieciom, natomiast w kopcu minimalnym (ang. min-heap) każdy rodzic ma wartość mniejszą lub równą swoim dzieciom. Dzięki tej właściwości sterta pozwala w bardzo krótkim czasie zidentyfikować element o największym lub najmniejszym priorytecie, co czyni ją idealną podstawą do implementacji kolejki priorytetowej.
Jednym z podstawowych typów struktur danych są właśnie kolejki priorytetowe, które przechowują elementy zbioru, na którym zdefiniowana jest relacja porządku. Każdemu elementowi przypisuje się klucz (priorytet), według którego ustalana jest kolejność operacji. W przeciwieństwie do zwykłej kolejki, gdzie elementy są usuwane w kolejności ich wstawienia (FIFO), w kolejce priorytetowej elementy są zdejmowane na podstawie wartości klucza. Wyróżniamy dwa główne typy takich kolejek: kolejki typu max, gdzie usuwany jest element o największym priorytecie, oraz kolejki typu min, w których priorytet ma wartość najmniejsza.
Kolejną metodą przydatną do operowania na kopcu jest dodawanie do niego elementów. Dodawanie nowego elementu do kolejki priorytetowej opartej na kopcu maksymalnym polega na wstawieniu go jako nowego liścia na najniższym, najbardziej prawym wolnym miejscu w drzewie (czyli na końcu tablicy reprezentującej stertę). Jednak po takim dodaniu własność kopca może być naruszona, jeśli nowy element ma większy klucz niż jego ojciec. W takiej sytuacji należy przywrócić poprawną strukturę kopca poprzez tzw. „wynurzanie się” elementu – czyli przesuwanie go w górę drzewa przez zamiany z jego rodzicem aż do momentu, gdy znajdzie się w odpowiednim miejscu (lub zostanie korzeniem). Ten proces można przeprowadzić na dwa sposoby:
Skoro poznaliśmy już procedurę przywracania własności kopca, możemy przejść do pytania, w jaki sposób zbudować stertę z danych znajdujących się w tablicy, o których nic nie wiemy – to znaczy danych, które nie są w żaden sposób uporządkowane i nie spełniają warunku kopca. Co istotne, elementy tablicy tworzą logicznie strukturę drzewa binarnego, lecz bardzo rzadko jest ona od razu stertą. Aby utworzyć poprawną strukturę kopca, należy zadbać o to, by każde z poddrzew tej struktury spełniało własność kopca – a więc by każdy węzeł był większy (w przypadku kopca maksymalnego) od swoich dzieci. Pomysł polega na zastosowaniu metody przywrocWlasnoscKopca (heapify) dla każdego węzła wewnętrznego, zaczynając od najniższego poziomu drzewa, aż po korzeń. Ponieważ liście są już jednoelementowymi drzewami, które z definicji są kopcami, nie wymagają przetwarzania. Dlatego wystarczy rozpocząć od ostatniego węzła, który posiada dzieci, czyli od indeksu ⌊n/2⌋ − 1 (gdzie n to liczba elementów w tablicy), i wykonywać heapify w kolejnych krokach dla wszystkich poprzedzających go indeksów, aż do 0. W ten sposób, przekształcając najpierw najmniejsze poddrzewa, a następnie coraz większe, aż do całego drzewa, otrzymujemy strukturę spełniającą warunek kopca. Poniżej zamieszczony jest kod C++ do budowy kopca z tablicy zawierające liczby w dowolnej kolejności.
Jednym z podstawowych typów struktur danych są właśnie kolejki priorytetowe, które przechowują elementy zbioru, na którym zdefiniowana jest relacja porządku. Każdemu elementowi przypisuje się klucz (priorytet), według którego ustalana jest kolejność operacji. W przeciwieństwie do zwykłej kolejki, gdzie elementy są usuwane w kolejności ich wstawienia (FIFO), w kolejce priorytetowej elementy są zdejmowane na podstawie wartości klucza. Wyróżniamy dwa główne typy takich kolejek: kolejki typu max, gdzie usuwany jest element o największym priorytecie, oraz kolejki typu min, w których priorytet ma wartość najmniejsza.
Kolejka priorytetowa musi być zaimplementowana w taki sposób, aby można było wykonywać na niej niżej wymienione operacje:
• Insert(S, x) – wstawienie elementu x do kolejki S
• FindMax(S) – poszukiwanie w kolejce S elementu o największym kluczu; funkcja zwraca ten element jako wynik
• DelMax(S) – usunięcie z kolejki S elementu o największym kluczu; funkcja zwraca ten element jako wynik

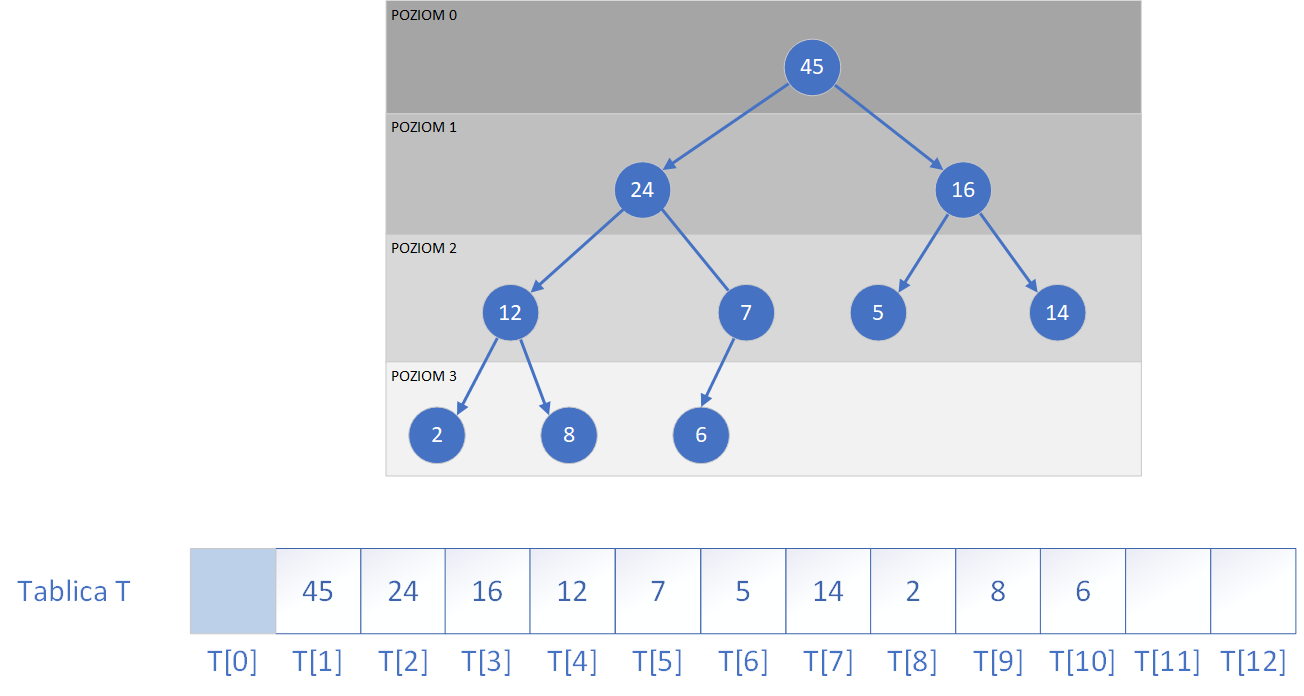
Każdy węzeł w kopcu ma co najwyżej dwie odnogi - tzw. potomków (synów).
Jeżeli na danym poziomie wszystkie miejsca są zapełnione oznacza to że drzewo jest pełne na danym poziomie. Jedynie ostatni poziom może nie być wypełniony do końca. Widzimy też, że kopiec jest często implementowany jako tablica jednowymiarowa, w której elementy drzewa binarnego zapisywane są kolejno w taki sposób, by zachować zależności rodzic–dziecko. Dzięki temu możliwe jest odwzorowanie struktury drzewa bez użycia wskaźników, a dostęp do poszczególnych węzłów oraz ich potomków może być realizowany za pomocą prostych obliczeń indeksów.
Mianowicie, jeśli interesujący nas węzeł znajduje się w tablicy pod indeksem i, to:
- indeks jego ojca (rodzica) to ⌊i / 2⌋, czyli część całkowita z połowy wartości i (dla i > 1),
- indeks lewego potomka wynosi 2 * i,
- indeks prawego potomka wynosi 2 * i + 1.
Możemy zdefiniować następującą własność kopca przechowanego w tablicy T:
T[i] ≤ T[indeksOjca(i)]
co oznacza, że każdy element w kopcu ma wartość nie większą niż jego ojciec.
Dzięki wykorzystaniu tej definicji możemy skonstruować algorytm, który będzie sortował wartości w tablicy. Wiemy, że zawsze w korzeniu drzewa kopca będzie przechowywana największa wartość. Jeżeli będziemy pobierać za każdym razem korzeń drzewa i umieszczać w tablicy posortowanych liczb to otrzymamy algorytm sortowania przez kopcowanie. Oczywiście brakuje nam jeszcze wiedzy w jaki sposób po pobraniu wartości korzenia drzewa przywrócić ponownie jego własności.
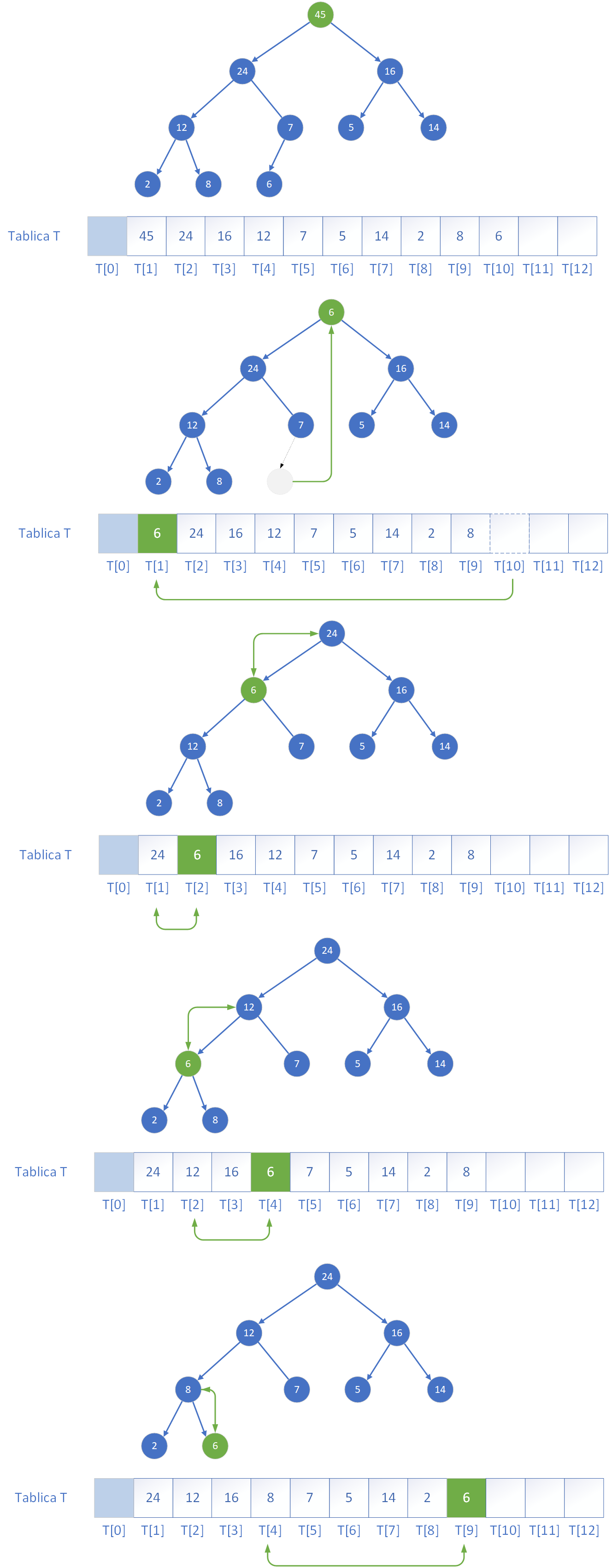
Jednym z mechanizmów utrzymujących strukturę sterty jest metoda przywracania własności kopca (ang. heapify). Jej zadaniem jest upewnienie się, że poddrzewo o korzeniu na danym indeksie i spełnia warunek kopca. W przypadku kopca maksymalnego oznacza to, że element znajdujący się na pozycji i powinien być nie mniejszy niż jego dzieci. Jeżeli warunek ten nie jest spełniony, to element i należy zamienić z większym z jego dwóch synów, co powoduje tzw. „spłynięcie w dół” (ang. sift down) danego elementu w hierarchii drzewa. Po takiej zamianie konieczne jest sprawdzenie poprawności struktury dla nowego położenia tego elementu, czyli rekursywne wywołanie funkcji dla odpowiedniego poddrzewa.
T[i] ≤ T[indeksOjca(i)]
co oznacza, że każdy element w kopcu ma wartość nie większą niż jego ojciec.
// Funkcja przywracająca własność kopca dla poddrzewa o korzeniu i
void heapify(vector<int>& T, int n, int i) {
int largest = i; // Zakładamy, że korzeń jest największy
int left = 2 * i + 1; // Indeks lewego dziecka
int right = 2 * i + 2; // Indeks prawego dziecka
// Jeśli lewe dziecko jest większe niż korzeń
if (left < n && T[left] > T[largest])
largest = left;
// Jeśli prawe dziecko jest większe niż największy dotąd
if (right < n && T[right] > T[largest])
largest = right;
// Jeśli największy nie jest korzeniem, zamień i kontynuuj
if (largest != i) {
swap(T[i], T[largest]);
heapify(T, n, largest); // Rekurencyjnie przywracaj własność kopca
}
}
// Pobiera największy element z kopca (korzeń) i przywraca strukturę
int extractMax(vector<int>& heap, int& size) {
if (size <= 0) throw out_of_range("Sterta jest pusta.");
int maxElement = heap[0]; // największy element (korzeń)
heap[0] = heap[size - 1]; // przenosimy ostatni element na początek
size--; // zmniejszamy rozmiar kopca
heapify(heap, size, 0); // przywracamy własność kopca od korzenia
return maxElement;
}

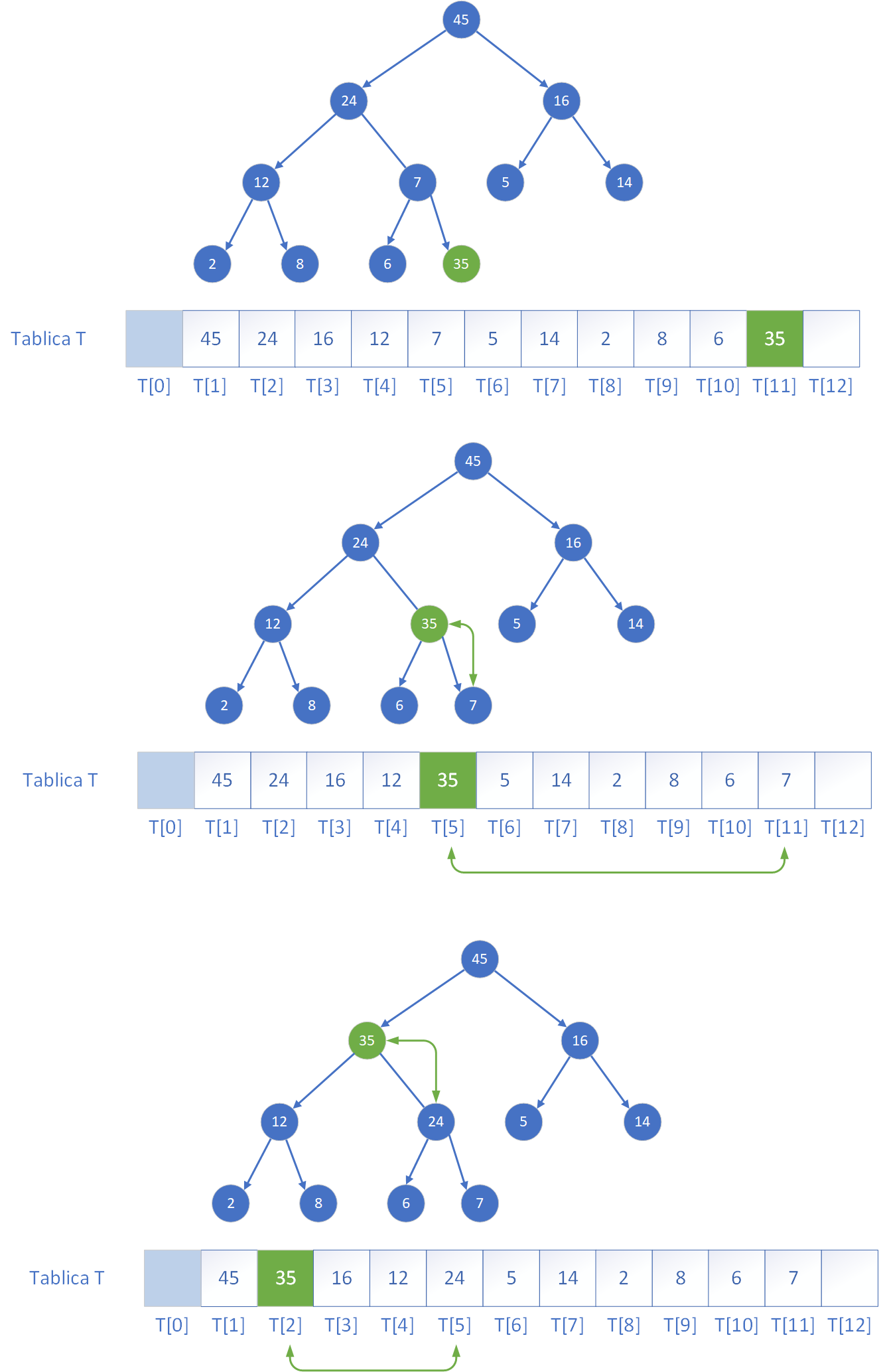
Kolejną metodą przydatną do operowania na kopcu jest dodawanie do niego elementów. Dodawanie nowego elementu do kolejki priorytetowej opartej na kopcu maksymalnym polega na wstawieniu go jako nowego liścia na najniższym, najbardziej prawym wolnym miejscu w drzewie (czyli na końcu tablicy reprezentującej stertę). Jednak po takim dodaniu własność kopca może być naruszona, jeśli nowy element ma większy klucz niż jego ojciec. W takiej sytuacji należy przywrócić poprawną strukturę kopca poprzez tzw. „wynurzanie się” elementu – czyli przesuwanie go w górę drzewa przez zamiany z jego rodzicem aż do momentu, gdy znajdzie się w odpowiednim miejscu (lub zostanie korzeniem). Ten proces można przeprowadzić na dwa sposoby:
void insert(vector<int>& heap, int& size, int value) {
size++;
int i = size - 1;
heap[i] = value;
while (i > 0 && heap[i] > heap[(i - 1) / 2]) {
swap(heap[i], heap[(i - 1) / 2]);
i = (i - 1) / 2;
}
}
void insert(vector<int>& heap, int& size, int value) {
size++;
int i = size - 1;
// Znalezienie miejsca na nowy element przez przesuwanie ojców w dół
while (i > 0 && value > heap[(i - 1) / 2]) {
heap[i] = heap[(i - 1) / 2];
i = (i - 1) / 2;
}
heap[i] = value;
}
Skoro poznaliśmy już procedurę przywracania własności kopca, możemy przejść do pytania, w jaki sposób zbudować stertę z danych znajdujących się w tablicy, o których nic nie wiemy – to znaczy danych, które nie są w żaden sposób uporządkowane i nie spełniają warunku kopca. Co istotne, elementy tablicy tworzą logicznie strukturę drzewa binarnego, lecz bardzo rzadko jest ona od razu stertą. Aby utworzyć poprawną strukturę kopca, należy zadbać o to, by każde z poddrzew tej struktury spełniało własność kopca – a więc by każdy węzeł był większy (w przypadku kopca maksymalnego) od swoich dzieci. Pomysł polega na zastosowaniu metody przywrocWlasnoscKopca (heapify) dla każdego węzła wewnętrznego, zaczynając od najniższego poziomu drzewa, aż po korzeń. Ponieważ liście są już jednoelementowymi drzewami, które z definicji są kopcami, nie wymagają przetwarzania. Dlatego wystarczy rozpocząć od ostatniego węzła, który posiada dzieci, czyli od indeksu ⌊n/2⌋ − 1 (gdzie n to liczba elementów w tablicy), i wykonywać heapify w kolejnych krokach dla wszystkich poprzedzających go indeksów, aż do 0. W ten sposób, przekształcając najpierw najmniejsze poddrzewa, a następnie coraz większe, aż do całego drzewa, otrzymujemy strukturę spełniającą warunek kopca. Poniżej zamieszczony jest kod C++ do budowy kopca z tablicy zawierające liczby w dowolnej kolejności.
// Buduje kopiec maksymalny z nieuporządkowanej tablicy
void buildMaxHeap(vector<int>& T) {
int n = T.size();
// Wywołujemy heapify od ostatniego rodzica do korzenia
for (int i = n / 2 - 1; i >= 0; i--) {
heapify(T, n, i);
}
}
