Podręcznik
Wymagania zaliczenia
Wersja podręcznika: 1.0
Data publikacji: 01.01.2022 r.
7. Przeszukiwanie tekstów
Przeszukiwanie tekstów stanowi jedno z fundamentalnych zagadnień algorytmicznych. Występuje bardzo często w różnych zastosowaniach informatycznych. Polega ono na odnalezieniu wystąpień określonego wzorca (ciągu znaków) w dłuższym tekście. Problem ten występuje w wielu zastosowaniach np. w edytorach tekstu, czy wyszukiwarkach internetowych. Często stawiamy sobie pytanie: czy zadany ciąg znaków (wzorzec) występuje w tekście, a jeśli tak to gdzie? Najprostszym podejściem do tego problemu jest metoda naiwna, w której przesuwamy wzorzec znak po znaku przez tekst i porównujemy go z odpowiadającym fragmentem tekstu. Poniżej przedstawiono kod aplikacji realizujący taki naiwny algorytm wyszukiwania wzorców. Tego typu podejście często nazywane jest szukanie metodą Brute Force (czyli naiwną).
Z tego powodu zostały opracowane inne bardziej efektywne metody wyszukiwania wzorców w tekście np. algorytm Knutha-Morrisa-Pratta (KMP). Dzięki wcześniejszemu przetworzeniu wzorca pozwala uniknąć niepotrzebnych porównań. Wzorzec jest analizowany i na podstawie jego struktury tworzona jest tzw. tablica prefiksowa, dzięki której możliwe jest pomijanie niektórych znaków tekstu bez ponownego przeszukiwania. Algorytm KMP działa w czasie O(n + m).
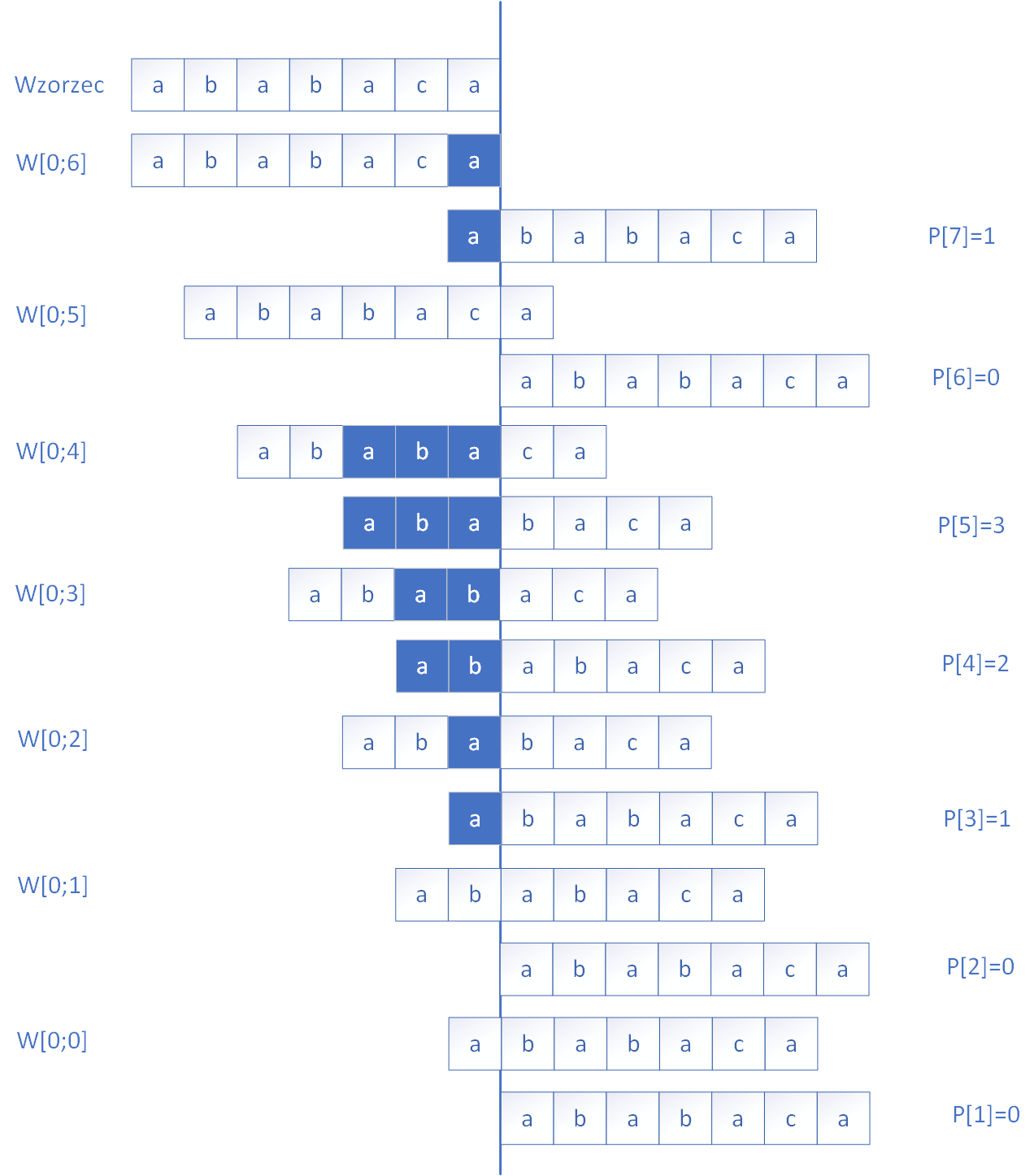
Podstawą algorytmu jest tzw. tablica P, która dla każdej pozycji i wzorca w[0..i] zawiera informację o długości najdłuższego prefiksu wzorca, który jest jednocześnie sufiksem tego fragmentu. Tablica ta pozwala algorytmowi "wiedzieć", ile początkowych liter wzorca można zachować po niezgodności, bez potrzeby rozpoczynania porównywania od początku. Budowa tej tablicy polega na porównywaniu kolejnych liter wzorca z jego początkiem i, jeśli występują dopasowania, zapisywaniu ich długości. W przypadku niezgodności algorytm cofa się w tablicy P, szukając krótszego dopasowania. Poniżej na rysunku zademonstrowano sposób wyznaczenia tablicy P dla przykładowego wzorca.
Po zbudowaniu tablicy prefiksowej P algorytm przystępuje do właściwego przeszukiwania tekstu. Wskaźnik i porusza się po tekście, a wskaźnik j – po wzorcu. Jeśli t[i] == w[j], porównywanie postępuje. W przypadku niezgodności KMP nie wraca w tekście, lecz sprawdza tablicę prefiksową i przesuwa wskaźnik j we wzorcu do pozycji podanej przez P[j−1], co pozwala natychmiast wznowić porównywanie od miejsca, gdzie znów istnieje potencjalna zgodność. Poniżej na przykładzie rysunkowym przedstawiono działanie algorytmu KMP dla przykładowego tekstu:
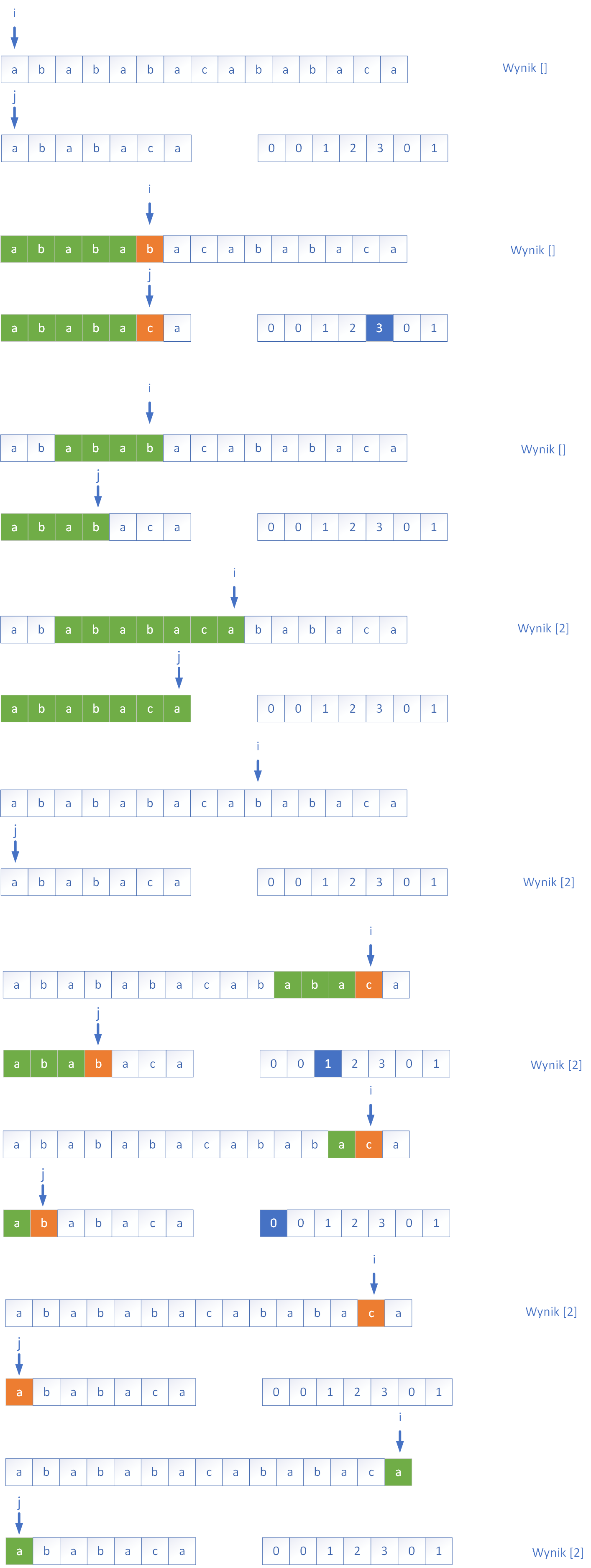
W przykładzie znaleziono tylko jedno miejsce o indeksie 2 w którym powtarza się szukany wzorzec.
int szukajBRF(const string& tekst, const string& wzorzec) {
int n = tekst.length();
int m = wzorzec.length();
for (int i = 0; i <= n - m; ++i) {
int j = 0;
while (j < m && tekst[i + j] == wzorzec[j]) {
j++;
}
if (j == m) return i; // znaleziono wzorzec w pozycji i
}
return -1; // nie znaleziono
}
Z tego powodu zostały opracowane inne bardziej efektywne metody wyszukiwania wzorców w tekście np. algorytm Knutha-Morrisa-Pratta (KMP). Dzięki wcześniejszemu przetworzeniu wzorca pozwala uniknąć niepotrzebnych porównań. Wzorzec jest analizowany i na podstawie jego struktury tworzona jest tzw. tablica prefiksowa, dzięki której możliwe jest pomijanie niektórych znaków tekstu bez ponownego przeszukiwania. Algorytm KMP działa w czasie O(n + m).
Podstawą algorytmu jest tzw. tablica P, która dla każdej pozycji i wzorca w[0..i] zawiera informację o długości najdłuższego prefiksu wzorca, który jest jednocześnie sufiksem tego fragmentu. Tablica ta pozwala algorytmowi "wiedzieć", ile początkowych liter wzorca można zachować po niezgodności, bez potrzeby rozpoczynania porównywania od początku. Budowa tej tablicy polega na porównywaniu kolejnych liter wzorca z jego początkiem i, jeśli występują dopasowania, zapisywaniu ich długości. W przypadku niezgodności algorytm cofa się w tablicy P, szukając krótszego dopasowania. Poniżej na rysunku zademonstrowano sposób wyznaczenia tablicy P dla przykładowego wzorca.

Po zbudowaniu tablicy prefiksowej P algorytm przystępuje do właściwego przeszukiwania tekstu. Wskaźnik i porusza się po tekście, a wskaźnik j – po wzorcu. Jeśli t[i] == w[j], porównywanie postępuje. W przypadku niezgodności KMP nie wraca w tekście, lecz sprawdza tablicę prefiksową i przesuwa wskaźnik j we wzorcu do pozycji podanej przez P[j−1], co pozwala natychmiast wznowić porównywanie od miejsca, gdzie znów istnieje potencjalna zgodność. Poniżej na przykładzie rysunkowym przedstawiono działanie algorytmu KMP dla przykładowego tekstu:

W przykładzie znaleziono tylko jedno miejsce o indeksie 2 w którym powtarza się szukany wzorzec.
