Podręcznik

Usuwanie elementów z drzewa binarnego wyszukiwania jest bardziej złożone niż ich dodawanie czy wyszukiwanie, ponieważ należy zadbać o to, aby struktura drzewa nadal spełniała warunki BST po usunięciu węzła. Zatem usuwanie drzewa rozpoczynamy od „likwidowania” liści, a kończymy na usunięciu liścia, który jest zarazem korzeniem drzewa. W celu utrzymania struktury drzewa, tuż przed usunięciem konkretnego liścia następuje ustawienie wskaźnika jego ojca (wskazującego do tej pory na ten liść) na wartość NULL. Proces ten przypomina klasyczne przechodzenie drzewa w porządku post-order, czyli: najpierw lewe poddrzewo, potem prawe, a na końcu bieżący węzeł. Dla każdego węzła rekurencyjnie wywołujemy procedurę usuwania jego dzieci, a dopiero po tym usuwamy sam węzeł. Tuż przed fizycznym usunięciem danego liścia należy ustawić wskaźnik ojca na NULL, co jest istotne dla utrzymania spójności struktury.

void deleteTree(Node* &root) {
    if (root == nullptr) return;

    // Rekurencyjnie usuwamy lewe i prawe poddrzewo
    deleteTree(root->left);
    deleteTree(root->right);

    // Usuwamy bieżący węzeł
    cout << "Usuwam węzeł: " << root->key << endl;
    delete root;
    root = NULL; // Ustawiamy wskaźnik na NULL, by „odłączyć” od ojca
}

Usuwanie pojedynczego węzła jest operacją bardziej złożoną. Istnieje kilka możliwości:

• Przypadek 1: Węzeł o zadanym kluczu nie istnieje - w tym przypadku funkcja przeszukująca drzewo nie odnajduje węzła o danym kluczu, więc nie zostaje wykonane żadne usunięcie. Drzewo pozostaje bez zmian.
  
• Przypadek 2: Węzeł ma co najwyżej jednego syna - jeśli usuwany węzeł nie posiada żadnych dzieci (jest liściem), można go bezpiecznie usunąć i przypisać NULL do wskaźnika jego ojca, który go wskazywał. Jeżeli węzeł ma tylko jedno dziecko, to usuwany węzeł można zastąpić wskaźnikiem do jego jedynego dziecka drzewo pozostaje poprawne, a usunięty węzeł znika z pamięci.
  
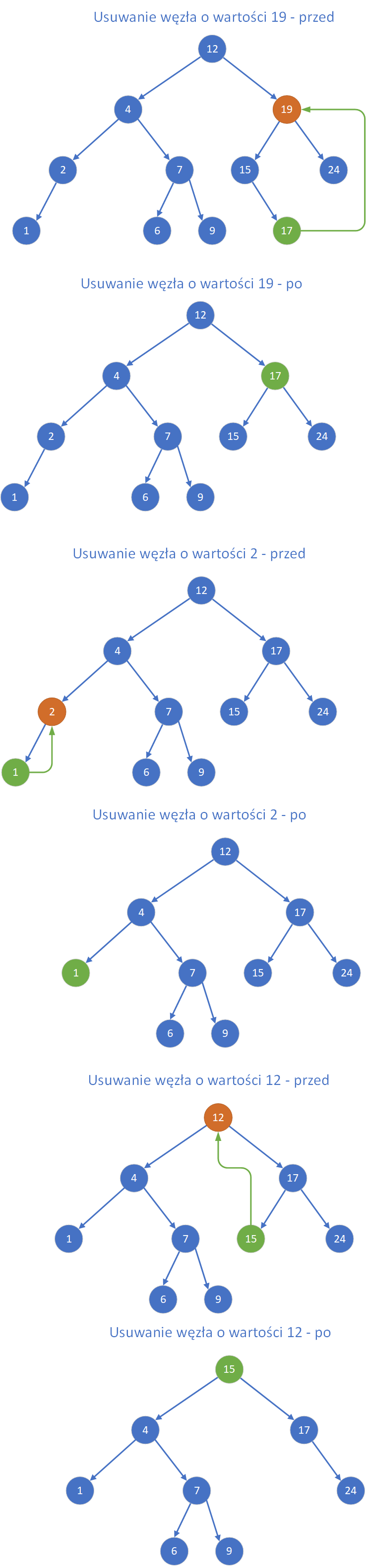
• Przypadek 3: Węzeł ma dwóch synów - to najtrudniejsza sytuacja, ponieważ węzeł nie może zostać po prostu usunięty bez naruszenia struktury drzewa. Dlatego stosujemy jedno z dwóch klasycznych rozwiązań: 
  • zastąpienie usuwanego węzła przez jego bezpośredniego następnika (successora), czyli najmniejszy element w jego prawym poddrzewie (najbardziej lewy węzeł z prawego poddrzewa). 
  • zastąpienie przez poprzednika (predecessora), czyli największy element w jego lewym poddrzewie (najbardziej prawy węzeł z lewego poddrzewa).

W celu dokładnego wyjaśnienia przypadku 3, który jest najbardziej skomplikowany poniżej znajduje się przykładowy rysunek demonstrujący sposoby usuwania węzłów z drzewa BST.