Podręcznik
Wymagania zaliczenia
Wersja podręcznika: 1.0
Data publikacji: 01.01.2022 r.
1. Drzewa binarnego wyszukiwania (BST)
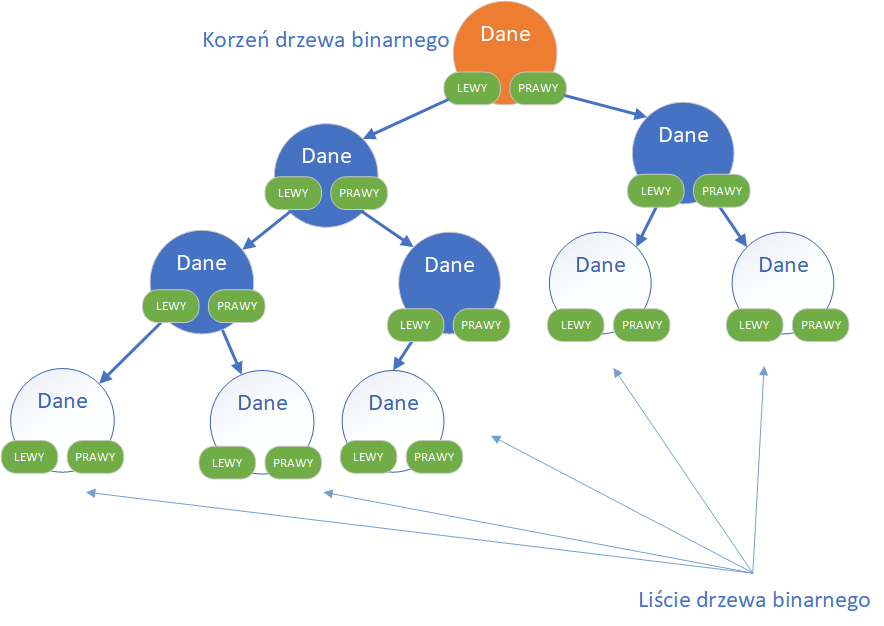
Bardzo ważną oraz często wykorzystywaną strukturą danych jest drzewo binarne. Jest to struktura hierarchiczna, w której każdy węzeł może mieć co najwyżej dwóch potomków. Zazwyczaj określa się ich jako lewy i prawy syn. Węzeł, który nie posiada żadnego potomka, nazywany jest liściem drzewa, natomiast węzeł bez poprzednika to korzeń drzewa.
Drzewa binarne są powszechnie stosowane w wielu dziedzinach, m.in. w algorytmach sortowania, wyszukiwania, kompresji danych (np. drzewa Huffmana) czy w systemach plików. Dzięki hierarchicznej budowie pozwalają na efektywną organizację i przeszukiwanie danych.
Drzewa binarne mogą być:
Na drzewie BST mozemy wykonywać podstawowe operacje takie jak: dodawanie węzła, usuwanie węzła oraz wyszukiwanie węzłą o podanej wartości. W kolejnych podrozdziałach przedsatwiono te podstawowe operacje.
Drzewa binarne mogą być:
- pełne – jeśli każdy węzeł ma 0 lub 2 dzieci,
- zupełne – jeśli wszystkie poziomy są zapełnione, oprócz ewentualnie ostatniego, który jest wypełniany od lewej,
- zrównoważone – gdy różnica wysokości lewego i prawego poddrzewa dla każdego węzła nie przekracza określonego limitu.

Każdy węzeł zawiera pole do przechowywania informacji oraz dwa wskaźniki. Jak widzimy, wskaźniki w węźle zostały nazwane mianem lewego oraz prawego – na ogół stosuje się właśnie takie nazewnictwo, w którym węzeł może mieć lewego oraz prawego syna. Ale węzeł w drzewie binarnym nie musi mieć obu synów – może nie mieć żadnego, może mieć również tylko jednego (lewego lub prawego).
Drzewa binarne są fundamentem wielu bardziej złożonych struktur np. drzewa binarnego przeszukiwania (ang. Binary Search Tree - BST). Drzewo binarnego wyszukiwania to specjalny typ drzewa binarnego, który wprowadza konkretną regułę porządkowania danych. Główną zaletą BST jest możliwość szybkiego wyszukiwania, wstawiania i usuwania elementów. W idealnym przypadku w czasie logarytmicznym.
Dla każdego węzła drzewa:
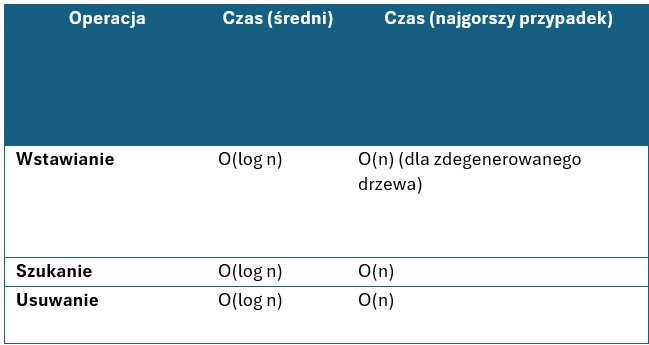
W tabeli poniżej przedstawiono złożoność obliczeniową poszczególnych operacji wykonywanych w drzewie BST.- wszystkie wartości w lewym poddrzewie są mniejsze niż wartość w tym węźle,
- wszystkie wartości w prawym poddrzewie są większe.
- każdy węzeł posiadał unikatową wartość danej - to bardzo ważne: elementy drzewa BST nie mogą się powtarzać!

Na drzewie BST mozemy wykonywać podstawowe operacje takie jak: dodawanie węzła, usuwanie węzła oraz wyszukiwanie węzłą o podanej wartości. W kolejnych podrozdziałach przedsatwiono te podstawowe operacje.
