Podręcznik

Krzyżowanie (ang. crossover) to kluczowy operator genetyczny odpowiedzialny za wymianę informacji pomiędzy osobnikami w populacji. Jego celem jest tworzenie nowych rozwiązań poprzez kombinację cech rodziców. Skuteczny operator krzyżowania powinien z jednej strony umożliwiać eksploatację dobrych rozwiązań, a z drugiej zachować wystarczającą różnorodność w populacji.

W zależności od rodzaju kodowania genotypu, stosuje się różne techniki krzyżowania. Poniżej przedstawiamy najważniejsze z nich.

Krzyżowanie dla kodowania binarnego (klasycznego)

Jednopunktowe (single-point crossover)

Losowany jest jeden punkt podziału chromosomu. Dzieci dziedziczą część genów od jednego rodzica przed punktem, a drugą część od drugiego rodzica.

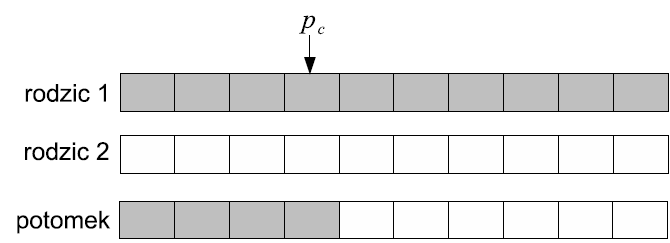
Dwupunktowe (two-point crossover)

Losowane są dwa punkty podziału. Fragment między nimi jest zamieniany pomiędzy rodzicami. Pozwala to na bardziej zróżnicowaną rekombinację.

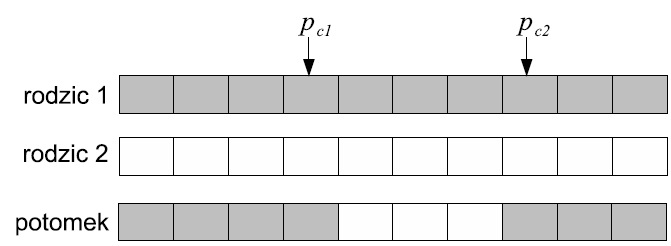
Jednorodne (uniform crossover)

Dla każdego genu losowo (z prawdopodobieństwem np. 0.5) wybierany jest jeden z rodziców. Zapewnia to największe wymieszanie cech.

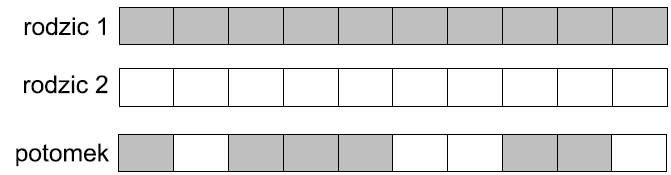
Zalety tych metod to prostota, niska złożoność i szerokie zastosowanie w kodowaniu binarnym. Wadą może być generowanie dziwnych struktur rozwiązań – operacje są niezależne od semantyki problemu.

Krzyżowanie dla kodowania rzeczywistego

Krzyżowanie arytmetyczne

Potomkowie wyznaczani są jako liniowa kombinacja rodziców:

$\text{Potomek} = \alpha \cdot \text{Rodzic}_1 + (1 - \alpha) \cdot \text{Rodzic}_2$

gdzie $\alpha \in [0,1]$ to losowy współczynnik.

Krzyżowanie blendowane (BLX-$\alpha$)}

Nowe geny losowane są z przedziału szerszego niż zakres między genami rodziców. Umożliwia eksplorację nowych wartości:

$x = U[\text{min} - d \cdot \alpha,\ \text{max} + d \cdot \alpha]$

gdzie $d = |x_1 - x_2|$.

Krzyżowanie z zakłóceniem (SBX)

Imituje rozkład krzyżowania binarnego, ale w przestrzeni ciągłej, operując bezpośrednio na liczbach rzeczywistych. Simulated Binary Crossover (SBX) jest zaprojektowany tak, aby zachowywać podobne statystyczne właściwości jak klasyczne krzyżowanie dwupunktowe, ale działa w przestrzeni rzeczywistej, co czyni go użytecznym w optymalizacji ciągłej. Główna idea polega na losowym generowaniu wartości potomnych wokół wartości rodziców z kontrolowaną zmiennością, regulowaną parametrem rozkładu (ang. distribution index).

SBX jest szczególnie popularny w strategiach ewolucyjnych i algorytmach różnicowych. Dzięki parametrowi rozkładu można kontrolować zakres eksploracji: niska wartość parametru sprzyja dużym odchyleniom (eksploracja), natomiast wyższe wartości skutkują generowaniem potomków bardzo bliskich rodzicom (eksploatacja). To czyni SBX elastycznym narzędziem, dobrze dostosowanym do różnych etapów procesu optymalizacji.

Krzyżowanie dla kodowania permutacyjnego

W przypadku permutacji, celem jest zachowanie unikalności elementów – klasyczne krzyżowanie nie może być stosowane. Zamiast tego stosujemy: 

Krzyżowanie cykliczne (CX)

Krzyżowanie cykliczne (CX) polega na identyfikowaniu pozycyjnych cykli pomiędzy dwoma rodzicami. Dla każdego osobnika wyznacza się cykl elementów, które w tych samych pozycjach znajdują się u obojga rodziców, zachowując ich wzajemne relacje. Potomkowie dziedziczą cyklicznie pozycje z jednego rodzica, a pozostałe wypełniają elementami z drugiego, z zachowaniem unikalności.

Metoda ta dobrze zachowuje strukturę pozycyjną oryginalnych rozwiązań i jest odporna na utratę informacji porządkowej. W porównaniu do innych operatorów dla permutacji, CX generuje poowy niż np. PMX czy OX, co czyni go dobrym wyborem tam, gdzie istotne jest zachowanie względnych pozycji w permutacjach.

Krzyżowanie PMX

Krzyżowanie PMX (Partially Mapped Crossover) polega na losowym wybraniu fragmentu permutacji z jednego z rodziców i bezpośrednim przepisaniu go do potomka. Następnie dla pozostałych pozycji stosowane jest odwzorowanie elementów z drugiego rodzica na podstawie zależności utworzonych przez wspólny fragment. Dzięki temu zachowana zostaje zgodność z permutacyjną strukturą – każdy element występuje tylko raz.

PMX dobrze radzi sobie z zachowaniem względnych pozycji i unikalności elementów, co czyni go popularnym w problemach typu TSP i alokacyjnych. Metoda ta jest bardziej „lokalna” niż krzyżowanie cykliczne – silniej zachowuje lokalne fragmenty jednego z rodziców, przez co umożliwia zarówno eksploatację, jak i pewien stopień eksploracji przestrzeni rozwiązań.

Order Crossover (OX)

Krzyżowanie OX (Order Crossover) to technika, która zachowuje porządek występowania elementów oraz ich względną kolejność. Proces polega na losowym wybraniu fragmentu permutacji z jednego rodzica i bezpośrednim przepisaniu go do potomka. Następnie, uzupełnia się pozostałe miejsca w chromosomie, przechodząc kolejno przez elementy drugiego rodzica, pomijając te już zapisane, zachowując ich oryginalną kolejność.

Metoda ta jest niezwykle skuteczna w zachowywaniu informacji o sąsiedztwie elementów – co jest istotne np. w problemach trasowania czy harmonogramowania. Pozwala na przenoszenie całych sekwencji z rodziców do potomków, co może wspomóc zachowanie lokalnych struktur rozwiązania, które wykazują dobrą jakość.

OX, w porównaniu do innych operatorów dla permutacji, takich jak PMX czy CX, lepiej nadaje się do problemów, gdzie kolejność elementów ma większe znaczenie niż ich konkretne pozycje. Jest także stosunkowo łatwy do zaimplementowania, co czyni go jednym z najpopularniejszych operatorów krzyżowania w problemach kombinatorycznych.

Krzyżowanie dla kodowania drzewiastego

Krzyżowanie poddrzew

Krzyżowanie poddrzew (subtree crossover) to najczęściej stosowany operator w programowaniu genetycznym. Działa poprzez losowe wybranie węzła w drzewie każdego z rodziców, a następnie zamianę odpowiadających im poddrzew. Operacja ta pozwala na generowanie potomków, którzy łączą elementy strukturalne obu rodziców, zachowując przy tym składniową poprawność wyrażeń.

Zaletą tego podejścia jest jego naturalność w kontekście drzewiastych reprezentacji – poddrzewa mogą reprezentować całe podfunkcje, wyrażenia lub bloki instrukcji. Dzięki temu krzyżowanie może wprowadzać znaczące zmiany w funkcjonalności osobników, co sprzyja eksploracji przestrzeni rozwiązań. Jednocześnie zachowuje spójność semantyczną potomków, co jest kluczowe dla unikania błędnych lub niekompilowalnych struktur.

Aby zapobiec nadmiernemu wzrostowi rozmiarów drzew (tzw. "bloat"), często stosuje się ograniczenia na maksymalną głębokość drzewa potomka lub kontroluje się prawdopodobieństwo wyboru węzłów w zależności od ich poziomu. Taka regulacja pozwala zachować równowagę między eksploracją a stabilnością populacji, ograniczając tworzenie zbyt dużych, trudnych do zinterpretowania struktur.

Krzyżowanie jedno- i wielopunktowe

Zamiast zamiany całych poddrzew, możliwa jest zamiana pojedynczych gałęzi lub zestawów gałęzi, zgodnie z zadanymi regułami syntaktycznymi. Taki sposób krzyżowania pozwala na bardziej precyzyjne operowanie strukturą drzewa – można np. wymieniać tylko konkretne operatory matematyczne, fragmenty wyrażeń lub konkretne funkcje warunkowe. Podejście to umożliwia drobniejsze i bardziej kontrolowane modyfikacje, co może być korzystne w końcowych etapach ewolucji, gdy poszukiwane są optymalne drobne zmiany.

Wersje jedno- i wielopunktowe krzyżowania na poziomie drzewa mogą także uwzględniać kontekst syntaktyczny, np. tylko zamianę węzłów o tej samej arności (liczbie argumentów) albo tej samej kategorii (np. operatorów logicznych). Zapewnia to zachowanie poprawności semantycznej i składniowej potomków oraz pozwala utrzymać strukturę kodu w granicach oczekiwanej złożoności. Dobrze zaprojektowane krzyżowanie na poziomie gałęzi może skutkować bardziej stabilną i przewidywalną ewolucją programu.

Te operatory pozwalają generować złożone struktury, np. funkcje matematyczne, ale wymagają kontroli poprawności składniowej potomków.

Inne techniki krzyżowania

Krzyżowanie heurystyczne

Tworzy potomek przesunięty w kierunku lepszego z rodziców:

$x = x_1 + r \cdot (x_1 - x_2)$

gdzie $$x_1$ jest lepszy od $x_2$, a $r$ – losowa liczba.

Krzyżowanie topologiczne

Krzyżowanie topologiczne znajduje zastosowanie przede wszystkim w algorytmach, które operują na strukturach grafowych, takich jak ewolucja architektury sieci neuronowych (neuroewolucja) czy optymalizacja połączeń logicznych. W takich przypadkach genotypem nie jest prosty ciąg bitów czy liczb, lecz graf reprezentujący połączenia pomiędzy węzłami (neurony, funkcje, jednostki przetwarzające). Krzyżowanie polega na łączeniu części struktury dwóch rodziców w sposób, który tworzy nową sensowną topologię – np. przez zachowanie wspólnych połączeń oraz wstawienie unikalnych fragmentów z każdego z rodziców.

Dla sieci neuronowych najczęściej krzyżowane są zarówno struktury połączeń (czyli które węzły są ze sobą połączone), jak i wagi tych połączeń. Przykładem jest algorytm NEAT (NeuroEvolution of Augmenting Topologies), który identyfikuje odpowiadające sobie węzły i połączenia poprzez mechanizm numerowania genów, a następnie tworzy potomka z części wspólnych oraz zmutowanych nowych połączeń. Dzięki temu możliwe jest ewolucyjne rozwijanie złożonych sieci, które zachowują funkcjonalność poprzedników.

Zaletą krzyżowania topologicznego jest możliwość tworzenia coraz bardziej zaawansowanych i nieliniowych architektur, jednak jego projektowanie wymaga dużej ostrożności. Istotne jest zachowanie poprawności strukturalnej (np. unikanie cykli w sieciach jednokierunkowych) oraz funkcjonalności potomków. Operatory te bywają złożone, ale stanowią fundament dla nowoczesnych metod neuroewolucyjnych i programowania strukturalnego.

Podsumowanie

Wybór operatora krzyżowania zależy bezpośrednio od typu kodowania i charakteru problemu. Odpowiedni operator powinien:

• zachowywać poprawność semantyczną rozwiązań,
• sprzyjać eksploracji i eksploatacji,
• być dopasowany do struktury genotypu.

W praktyce operator krzyżowania bywa kluczowym czynnikiem wpływającym na skuteczność algorytmu genetycznego. Dobór operatora często wymaga eksperymentalnej walidacji i dostosowania do konkretnego zadania.