Podręcznik: Jak to działa

4. Particle Swarm Optimization

4.1. Jak to działa

Na podstawie pracy Abrahama, Das i Roya (2007) można zidentyfikować kilka fundamentalnych powodów, dla których algorytmy rojowe – w szczególności PSO (Particle Swarm Optimization) – są skuteczne w rozwiązywaniu problemów optymalizacyjnych, zarówno w przestrzeniach dyskretnych, jak i ciągłych. Ich efektywność wynika z kombinacji prostoty lokalnych reguł, mechanizmów komunikacji oraz emergencji zachowań grupowych.

Proste zasady, złożone efekty

Jednym z najważniejszych argumentów przytoczonych przez Abrahama i współautorów jest to, że złożone wzorce mogą wyłaniać się z prostych zachowań jednostek. W PSO każda cząstka kieruje się tylko kilkoma regułami: porusza się po przestrzeni rozwiązań pod wpływem własnego najlepszego doświadczenia oraz najlepszej znalezionej dotąd pozycji w swoim otoczeniu. To wystarczy, by cała populacja, nawet w bardzo złożonym krajobrazie funkcji celu, stopniowo zbiegała się do optymalnych (lub bliskich optymalnym) regionów.

Wymiana informacji i adaptacja

Drugi kluczowy element skuteczności PSO to zdolność komunikacji i adaptacji. Cząstki nie działają niezależnie – dzielą się informacją. W zależności od zastosowanej topologii (np. sąsiedztwa globalnego lub lokalnego), każda cząstka może korzystać z doświadczenia innych. To „uczenie się od innych” sprawia, że zamiast losowego błądzenia, mamy do czynienia z kierunkowym przeszukiwaniem, przy jednoczesnym zachowaniu różnorodności.

Brak potrzeby informacji gradientowej

W klasycznych algorytmach optymalizacyjnych, jak np. metoda gradientu, potrzebna jest znajomość pochodnych funkcji celu. PSO, podobnie jak inne algorytmy ewolucyjne, działa wyłącznie na podstawie wartości funkcji celu, bez potrzeby jej analitycznego opisu. To sprawia, że PSO jest odporny na nieliniowości, nieciągłości i szum – a zatem doskonale sprawdza się tam, gdzie tradycyjne metody zawodzą.

Eksploracja vs. eksploatacja

Według Abrahama, Das i Roya algorytmy rojowe osiągają skuteczność dzięki naturalnemu balansowi między eksploracją (badaniem nowych obszarów przestrzeni) a eksploatacją (lokalnym udoskonalaniem znanych rozwiązań). Początkowo cząstki przemieszczają się bardziej chaotycznie, dzięki czemu mogą „zajrzeć” do wielu regionów. Z czasem jednak, gdy znajdą obiecujące obszary, ich ruch staje się bardziej skupiony i następuje zbieżność.

Elastyczność i skalowalność

PSO działa dobrze niezależnie od wymiarowości przestrzeni problemu i może być z łatwością dostosowany do różnych zastosowań. Autorzy podkreślają, że dzięki temu algorytmy rojowe są elastyczne, łatwe do implementacji i wydajne obliczeniowo – szczególnie w środowiskach, gdzie wiele jednostek może działać równolegle.

Przejdźmy zatem do formalnej definicji algorytmu PSO, zaczynając od założeń:

Założenia algorytmu PSO – co wie każda cząstka?

W algorytmie PSO (Particle Swarm Optimization) modelujemy rozwiązania problemu jako cząstki poruszające się w przestrzeni przeszukiwań. Każda z tych cząstek (zwanych też osobnikami) posiada zestaw cech, który pozwala jej podejmować decyzje na podstawie lokalnych i sąsiedzkich informacji.

Wiedza i pamięć cząstki

Każda cząstka w roju:

zna swoje aktualne położenie w przestrzeni (np. współrzędne),
potrafi ocenić jakość swojego położenia, czyli zna wartość funkcji celu w swoim punkcie,
porusza się z określoną prędkością i w zadanym kierunku,
zapamiętuje najlepsze położenie, jakie kiedykolwiek odwiedziła (tzw. pozycję własnego optimum),
zna wartość funkcji celu w tym najlepszym punkcie.

Interakcje społeczne

Cząstka nie działa w izolacji:

wie, kim są jej sąsiedzi – czyli z kim „wymienia się” informacją,
zna najlepsze pozycje osiągnięte przez sąsiadów,
zna też wartość funkcji celu w tych pozycjach.

Efekt emergentny

Ten zestaw prostych właściwości daje niesamowicie efektywne zachowanie: cząstki potrafią samodzielnie, bez centralnego sterowania, gromadzić się wokół optymalnych punktów przestrzeni.

Ten zestaw cech daje umiejętność skupiania się osobników czy zdolność znajdowania określonych punktów w przestrzeni.

Dzięki połączeniu pamięci własnej i „inteligencji zbiorowej” algorytm PSO jest w stanie skutecznie eksplorować przestrzeń rozwiązań, a jednocześnie zbiegać do punktów optymalnych.

Realizacja

Jeśli już mamy założenia, pora ubrać je w algorytm. Zakładamy więc, że każda cząstka lata w n-wymiarowej przestrzeni:

$x_i=[x_{i1}, x_{i2}, \ldots, x_{in}]^T x_{i}^{k+1}=x_i^k+v_i^k$
Pytanie skąd mamy wziąć prędkość?

Na to odpowiadają nam wcześniejsze założenia. A więc:
Każda cząstka porusza się z pewną inercją - nie chce zmieniać kierunku:

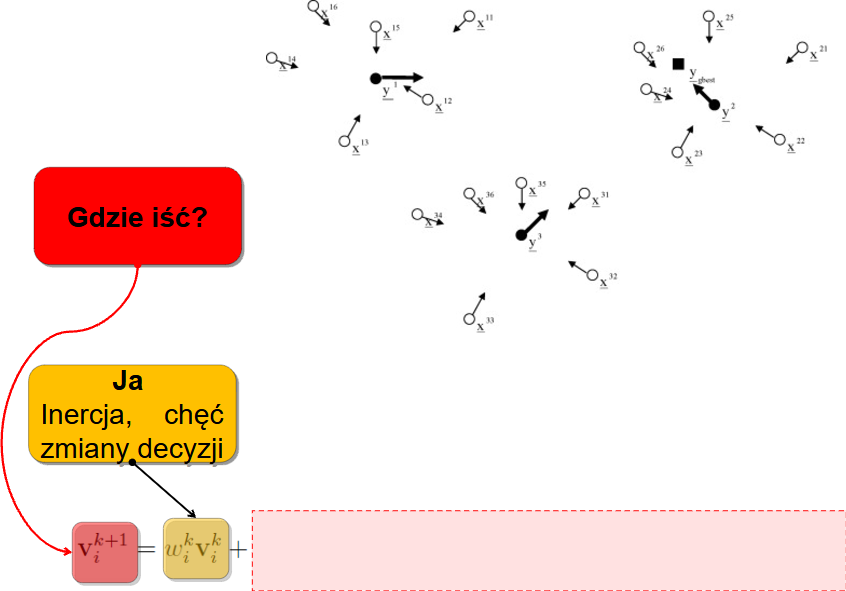
Każdy dąży też do miejsca gdzie mu było do tej pory najlepiej - więc mamy składową, która kieruje nas w miejsce najlepiej ocenione w historii konkretnej cząstki:

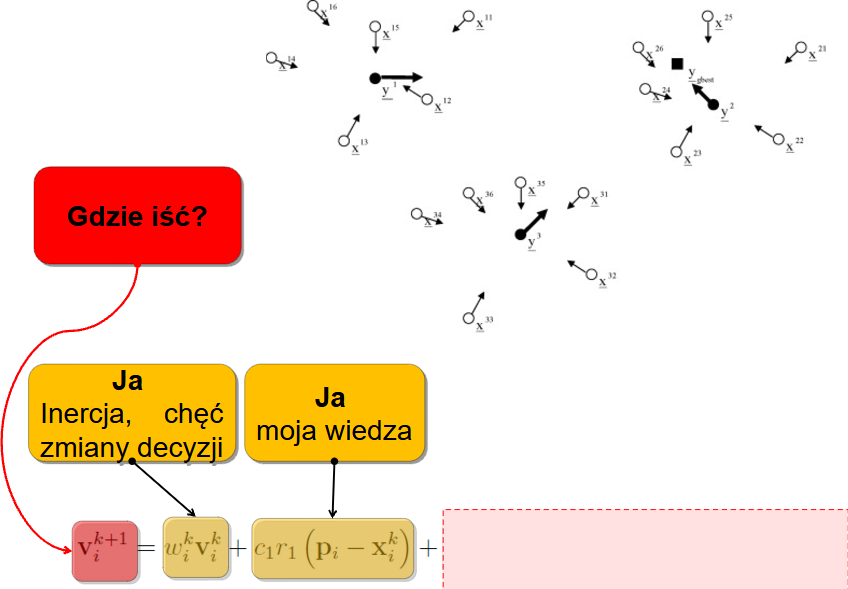
Założenie jednak mówiło, że nie tylko moja wiedza jest istotna - także mam dzielić się informacjami z innymi. Mogę więc podglądać sąsiadów:

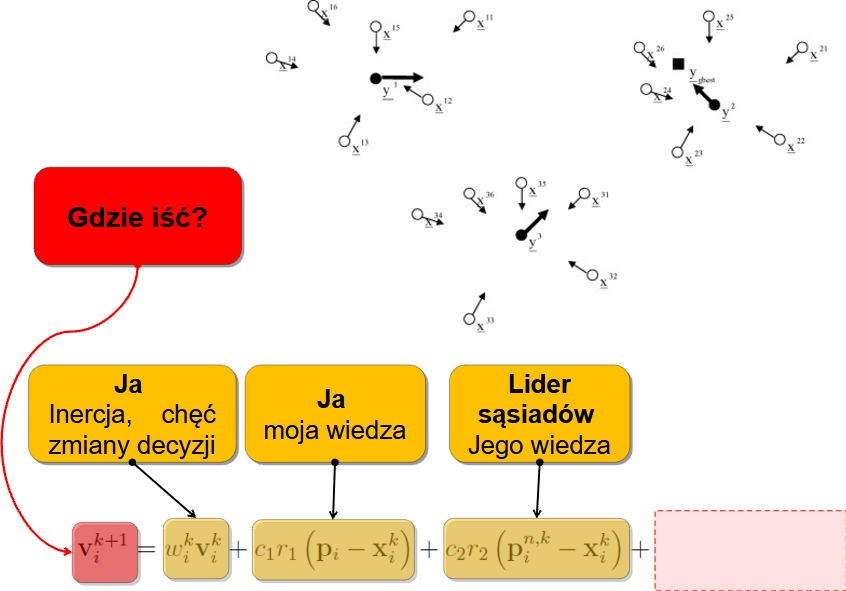
No i - last but not least - mogę patrzeć na ideały, czyli podążać w kierunku definiowanym przez najlepszą cząstkę w całym roju:

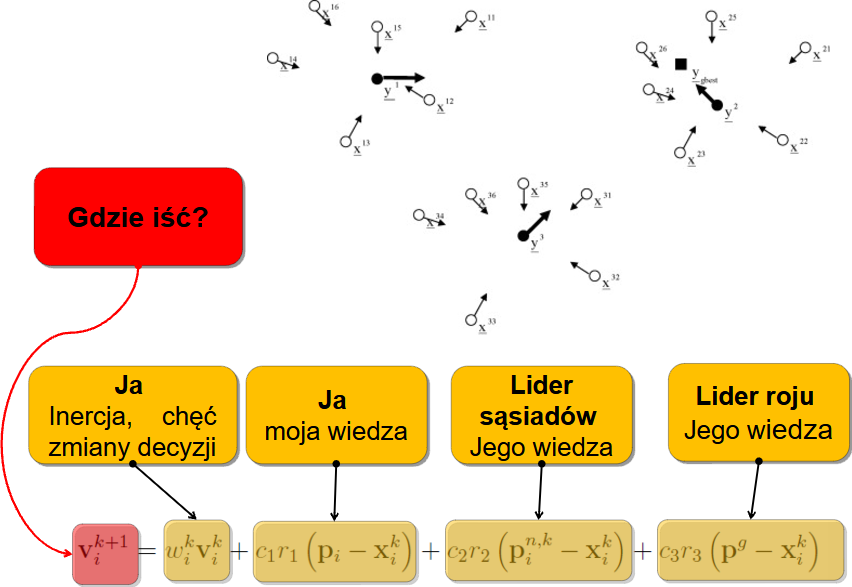
I to już całe wyrażenie które kieruje ruchem każdej cząstki. Finalnie więc mamy wyrażenie:

$v_i^{k+1}=w_i^k v_i^k + c_1 r_1(p_i-x_i^k)+c_2r_2(p_i^{n,k}-x_i^k)+c_3r_3(p^{g}-x_i^k)$

v_i(t+1) = \omega \cdot v_i(t) + c_1 \cdot r_1 \cdot \left(p_i - x_i(t)\right) + c_2 \cdot r_2 \cdot \left(g_i - x_i(t)\right)

gdzie:

$v_i^k$ – prędkość cząstki i w chwili k,
$x_i^k$ - aktualna pozycja cząstki i.
$p_i$ - najlepsza dotąd pozycja cząstki i
$p_i^{n,k}$ - najlepsza pozycja w sąsiedztwie cząstki
$p^g$ - najlepsza w ogóle pozycja w roju,
$w$ - współczynnik inercji
$c_1,c_2, c_3$ - współczynniki socjalne (przyciąganie do własnego, lokalnego i globalnego optimum)
$r_1,r_2, r_3$ - wartości losowe generowane niezależnie dla każdego wymiaru i każdej cząstki