Podręcznik

Jednym z kluczowych pojęć w algorytmie PSO jest sąsiedztwo (ang. neighborhood). O ile w algorytmach genetycznych osobniki współpracują przez mechanizmy doboru, krzyżowania i mutacji, to w PSO wymiana informacji opiera się na obserwacji – każda cząstka aktualizuje swoje zachowanie na podstawie wyników innych cząstek, które zna. Ale których konkretnie? Tu właśnie wkracza pojęcie sąsiedztwa.

Dlaczego sąsiedztwo jest ważne?

W klasycznej wersji PSO każda cząstka ma dostęp do najlepszego rozwiązania ze wszystkich cząstek w populacji. To podejście nazywane jest topologią globalną. Choć skuteczne, niesie ono pewne ryzyko: bardzo szybka zbieżność może prowadzić do utknięcia w minimum lokalnym. Dlatego wprowadzono alternatywy, w których cząstka zna tylko pewien wycinek populacji – czyli swoje sąsiedztwo.

Odpowiednie zdefiniowanie sąsiedztwa pozwala osiągnąć kompromis między:

• eksploracją (szukanie nowych rozwiązań),
• eksploatacją (dopieszczanie już znanych dobrych wyników).

Innymi słowy: sąsiedztwo to mechanizm, który równoważy rozbieganie się roju i jego skupianie się wokół obiecujących punktów.

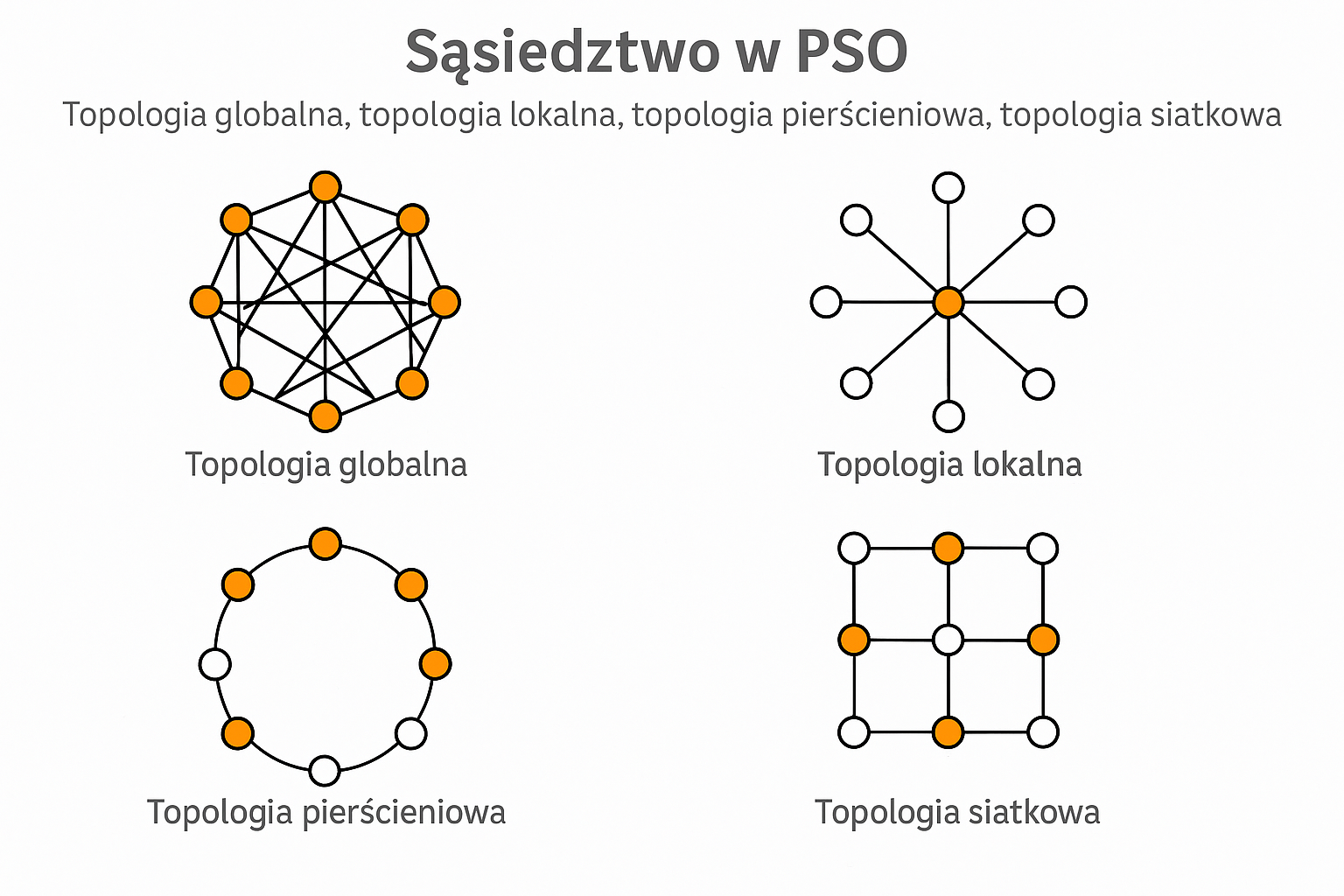
Rodzaje topologii sąsiedztwa

W praktyce najczęściej stosuje się trzy główne rodzaje topologii:

Topologia globalna (gBest)

Najprostszy wariant: każda cząstka zna najlepsze rozwiązanie znalezione przez dowolną cząstkę w populacji. Oznacza to, że każda z nich ma ten sam „punkt odniesienia społecznego”.

Zalety:

• bardzo szybka zbieżność (mała liczba iteracji do znalezienia rozwiązania),
• skuteczna, gdy krajobraz funkcji celu nie jest zbyt zdradliwy (np. niewiele ekstremów lokalnych).

Wady:

• ryzyko przedwczesnej zbieżności – gdy cząstki „za szybko” skupią się wokół lokalnego optimum, ignorując resztę przestrzeni.

Topologia lokalna (lBest)

Tutaj każda cząstka zna tylko cząstki ze swojego lokalnego sąsiedztwa. To może być np. grupa kilku sąsiadów z lewej i prawej strony (na przykład w sensie indeksów na liście populacji), lub osobniki znajdujące się najbliżej w przestrzeni.

Zalety:

• większa różnorodność ruchów w populacji – różne cząstki podążają za różnymi liderami,
• mniejsze ryzyko utknięcia w minimum lokalnym,
• dobra równowaga między eksploracją a eksploatacją.

Wady:

• wolniejsza zbieżność (więcej iteracji potrzebnych do osiągnięcia rozwiązania),
• większy koszt obliczeniowy, jeśli sąsiedztwo jest dynamicznie aktualizowane w przestrzeni (np. na podstawie odległości).

Topologia pierścieniowa

To szczególny przypadek topologii lokalnej. Zakładamy, że cząstki są ustawione w pierścień, a każda cząstka zna tylko kilku sąsiadów po lewej i prawej stronie. Przykład: jeśli liczność populacji to $N$, a liczba sąsiadów to 2, to cząstka $i$ zna cząstki $(i-1) \mod N$ i $(i+1) \mod N$.

Zalety:

• bardzo stabilna zbieżność,
• dobre zachowanie w problemach wielowymiarowych.

Inne, mniej klasyczne topologie

Choć powyższe trzy typy dominują w praktyce, w literaturze spotyka się też inne:

Topologia siatkowa (2D grid)

Cząstki są rozłożone w siatce (np. 10×10), a każda zna tylko najbliższych sąsiadów (góra, dół, lewo, prawo). Działa podobnie jak pierścień, ale w dwóch wymiarach.

Topologia dynamiczna

Sąsiedztwo cząstki może się zmieniać w czasie – np. zależnie od aktualnej odległości od innych cząstek, wyników funkcji celu, czy losowych fluktuacji. Takie podejście może symulować zjawiska naturalne, jak np. tymczasowe grupowanie się ławic ryb w obliczu drapieżnika.

Topologie hybrydowe

W rzeczywistych zastosowaniach czasem łączy się różne podejścia: np. globalne sąsiedztwo w pierwszych iteracjach, a lokalne w późniejszych. Takie strategie zwiększają szanse na skuteczne odnalezienie optimum globalnego.

Sąsiedztwo jako parametr algorytmu

Topologia sąsiedztwa można traktować jako hiperparametr – coś, co nie jest optymalizowane przez sam PSO, ale co można dobrać eksperymentalnie (lub przez metody metaoptymalizacyjne, np. algorytmy genetyczne lub grid search). Dobór sąsiedztwa może mieć ogromny wpływ na wydajność algorytmu, zwłaszcza w problemach wielomodalnych lub wysokowymiarowych.

W algorytmie PSO pojęcie sąsiedztwa pełni rolę kanału wymiany informacji. Cząstki nie potrzebują znać całej populacji – wystarczy, że obserwują lokalne otoczenie. To właśnie różnorodność możliwych topologii daje PSO elastyczność w dopasowywaniu się do różnych typów problemów: od gładkich funkcji z jednym optimum, po chaotyczne krajobrazy z wieloma pułapkami lokalnymi.

Dobór odpowiedniej topologii to jak wybór strategii przeszukiwania: czy lepiej iść za tłumem, czy trzymać się własnej ścieżki i lokalnych znajomych? Odpowiedź zależy od tego, jak wygląda przestrzeń problemu – a tu nie ma jednej recepty. Ale dobrze rozumiane sąsiedztwo to klucz do sukcesu w algorytmach rojowych.