Podręcznik: Rozmywanie

3. Modelowanie rozmyte

3.5. Rozmywanie

Rozmywaniem będziemy określali operację przekształcenia wielkości ostrej do postaci rozmytej.

$u\Rightarrow u^F$	(100)

gdzie: $u$ – wielkość ostra, $u^F$ – wielkości rozmyta.

W praktyce operacja rozmywania realizowalna jest w stosunkowo prosty sposób. Algorytm rozmywania jest następujący:

Krok 1 (formalny)
Przyporządkować każdej wielkości ostrej nazwę lingwistyczną.
Krok 2 (projekt zbiorów rozmytych)
Przyporządkować każdej wielkości ostrej wartości w postaci znormalizowanych zbiorów rozmytych. Przyporządkować unikalne etykiety lingwistyczne do każdego zbioru rozmytego.
Krok 3 (wyznaczenie wartości rozmytej)
Na podstawie znajomości wartości wielkości ostrej oraz znajomości zbiorów rozmytych przyporządkowanych tej wielkości (Krok 2) wyznaczyć wartości funkcji przynależności dla wszystkich tych zbiorów odpowiadających wartości rozmywanej wielkości ostrej.

Jak łatwo zauważyć, jeśli zmiennej ostrej przyporządkujemy n zbiorów rozmytych, to w wyniku operacji rozmywania każdej wartości tej wielkości ostrej przyporządkowana jest n wartości funkcji przynależności. Zgodnie z definicją rozmywania, wszystkie wartości wszystkich funkcji przynależności należą do przedziału domkniętego obustronnie $[0, 1]$ .

Rozmywanie

Niech wielkością ostrą będzie sygnał odchyłki regulacji $e\in \left\{E\right\}$ będący różnicą pomiędzy wartością zadaną i wartością mierzoną.

Krok 1 (formalny)
Odchyłce $e$ nadamy etykietę < odchyłka regulacji > i będziemy dalej traktować ją jako zmienną lingwistyczną.
Krok 2 (projekt zbiorów rozmytych)
Zmiennej lingwistycznej < odchyłka regulacji > przyporządkujmy trzy wartości: < ujemna odchyłka regulacji >, < zerowa odchyłka regulacji > i < dodatnia odchyłka regulacji >. Każda z wartości zmiennej lingwistycznej < odchyłka regulacji > jest zbiorem rozmytym o określonej funkcji przynależności lecz zdefiniowanej tej samej przestrzeni rozważań. Przestrzenią rozważań jest w tym przypadku zbiór wartości odchyłek regulacji. Dla uproszczenia zapisu wartościom zmiennej lingwistycznej < odchyłka regulacji > przyporządkujmy odpowiednio symbole $N$ , $Z$ i $P$ .
Krok 3 (wyznaczenie wartości rozmytej)
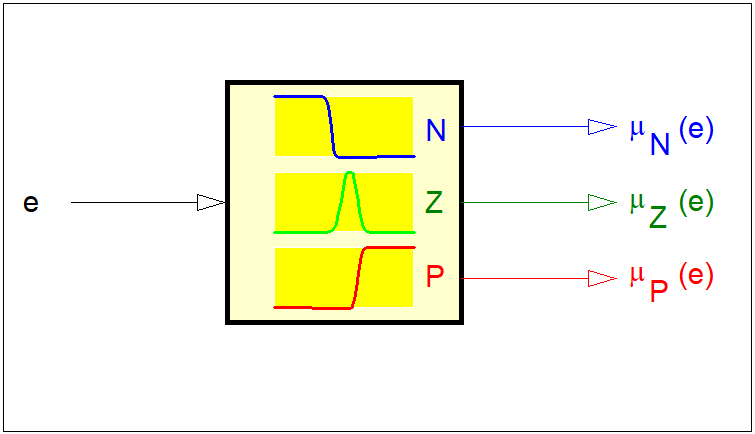
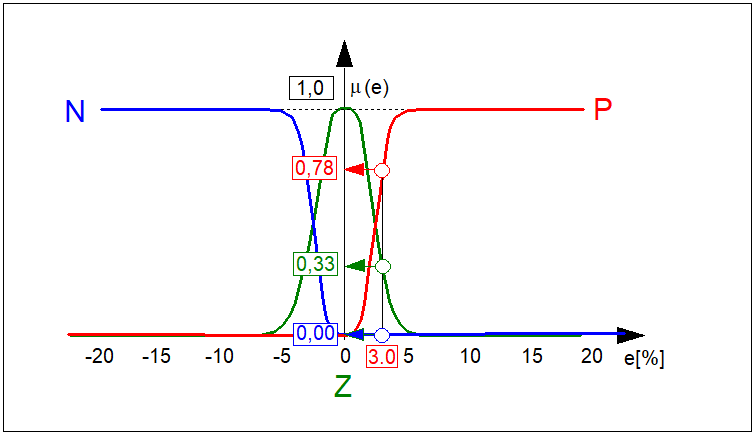
Załóżmy, że wartość odchyłki regulacji w pewnej chwili czasowej wynosi $e=3,0%$ (por. Rys. 13). Odchyłce tej odpowiadają wartości funkcji przynależności \( \left\{0,00, 0,33, 0,78 \right\} odpowiednio zbiorów $N$ , $Z$ i $P$ . Zatem operację rozmywania możemy w tym przypadku przedstawić w postaci:

$e(0,03)\Rightarrow \left\{0,00 , 0,33 , 0,78\right\}$ (101)

Podobnie można wyznaczyć odpowiednie trójki dla każdej wartości $e\in \left\{E\right\}$ . Operację rozmywania można przedstawić w postaci blokowej jak na Rys. 14.

Przykład operacji rozmywania odchyłki regulacji... — Rys. 13. Przykład operacji rozmywania odchyłki regulacji $e=3%$ . Funkcje przynależności:
- $\mu_N(e)$ zbioru rozmytego $N$ (*< ujemna odchyłka regulacji >*),
- $\mu_Z(e)$ zbioru rozmytego $Z$ (*< zerowa odchyłka regulacji >*),
- $\mu_P(e)$ zbioru rozmytego $P$ (*< dodatnia odchyłka regulacji >*).

Rys. 13. Przykład operacji rozmywania odchyłki regulacji $e=3%$ . Funkcje przynależności:
- $\mu_N(e)$ zbioru rozmytego $N$ (*< ujemna odchyłka regulacji >*),
- $\mu_Z(e)$ zbioru rozmytego $Z$ (*< zerowa odchyłka regulacji >*),
- $\mu_P(e)$ zbioru rozmytego $P$ (*< dodatnia odchyłka regulacji >*).

Schemat operacji rozmywania odchyłki regulacji... — Rys. 14. Schemat operacji rozmywania odchyłki regulacji $e$ . Oznaczenia jak na Rys. 13.

Rys. 14. Schemat operacji rozmywania odchyłki regulacji $e$ . Oznaczenia jak na Rys. 13.