Podręcznik
Wstęp do logiki rozmytej
3. Modelowanie rozmyte
3.6. Maszyna wnioskująca
W wyniku operacji rozmywania każdej wartości ostrej przyporządkowany zostaje zbiór ostrych wartości funkcji przynależności wszystkich zbiorów rozmytych przyporządkowanych rozmywanej wielkości ostrej.
Wartości rozmyte (zbiory rozmyte) nazywane są termami lub etykietami lingwistycznymi. Dla przykładu etykieta < zerowa odchyłka regulacji > jest wartością rozmytą zmiennej lingwistycznej < odchyłka regulacji >. Podobnie etykieta < niski poziom cieczy w zbiorniku > jest wartością rozmytą zmiennej lingwistycznej < poziom cieczy w zbiorniku > czy etykieta < zbyt szybkie narastanie ciśnienia pary > jest wartością zmiennej < narastanie ciśnienia pary >. W istocie etykieta zmiennej lingwistycznej może określać pewną jej cechę (atrybut), zaś wartości funkcji przynależności przypisanej etykiecie - intensywność tej cechy.
Maszyna wnioskująca realizuje proces wnioskowania z zastosowaniem reguł właściwych danej logice. Rozmyta maszyna wnioskująca prowadzi proces wyznaczania wniosków rozmytych na podstawie:
- przesłanek (wejść) rozmytych,
- reguł wnioskowania,
- logiki (sposobu) ewaluacji przesłanek.
W przypadku wnioskowania rozmytego zarówno przesłanki jak i wnioski mają charakter rozmyty. Wejściami maszyny wnioskującej w tym przypadku są przesłanki rozmyte, a wyjściami wnioski rozmyte. Mapowanie wejść na wyjścia w maszynie wnioskującej przebiega zgodnie z regułami i logiką przetwarzania przesłanek. Zestaw reguł tworzy tzw. bazę reguł. Jeśli znane są wszystkie relacje pomiędzy wszystkimi przesłankami i wszystkimi wnioskami to baza reguł nazywana jest bazą zupełną.
Liczba reguł bazy zupełnej zależna jest od:
- liczby wejść ostrych,
- liczby zbiorów rozmytych przyporządkowanych każdemu wejściu ostremu.
Uwagi:
- Liczba reguł bazy zupełnej zależy wyłącznie od liczności wejść rozmytych.
- Liczba wyjść rozmytych bazy zupełnej nie przekracza liczby reguł.
Dla układu rozmytego o \( n \) wejściach ostrych, z których każde zostało rozmyte na \( k_i \) zbiorów rozmytych liczba reguł bazy zupełnej wynosi:
| \( r=\prod_{i=1}^n k_i \) | (102) |
|---|
Liczba reguł bazy zupełnej
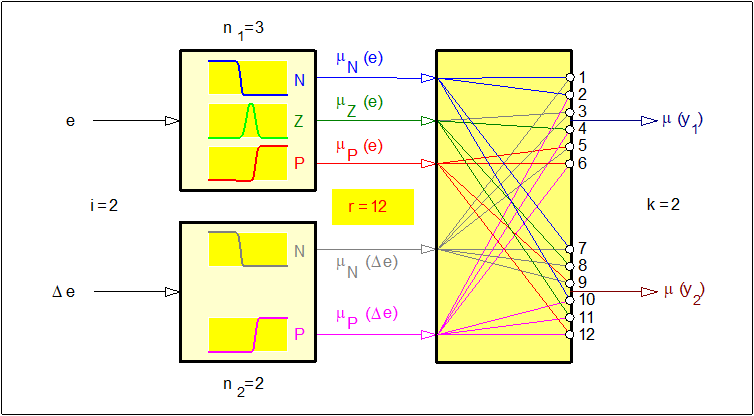
Załóżmy (Rys. 15), że mamy do czynienia z układem rozmytym o dwóch wejściach ostrych. Do każdego wejścia ostrego zostało przyporządkowane odpowiednio: \( k_1=3 \) i \( k_2=2 \) zbiorów rozmytych. Liczba reguł bazy zupełnej zgodnie ze wzorem (102) liczy:
\( r=k_1\times k_2=3\times 2=6 \)
Liczba reguł bazy zupełnej jest istotna z punktu widzenia zastosowań praktycznych. Im większa jest liczba tych reguł, tym proces wnioskowania jest bardziej złożony i kosztowny obliczeniowo. Dla przykładu w przypadku układu rozmytego o trzech wejściach ostrych i w którym każdemu z wejść przyporządkowano tylko po 5 zbiorów rozmytych powoduje, że liczba reguł bazy zupełnej zgodnie z formułą (102) rośnie do 125. Tak znaczna liczba reguł stanowi istotny czynnik wydłużający realizację operacji rozmywania, wnioskowania i wyostrzania. Liczba reguł w jakimś sensie może być wskaźnikiem pomocnym do oceny mocy obliczeniowych koniecznych do realizacji regulatora rozmytego. Jest to szczególnie ważne w układach czasu rzeczywistego w sterowaniu procesów krytycznych czasowo np. w układach sterowania antypoślizgowego ASR. W przypadkach sterowania procesów krytycznych czasowo stosowane jest również wnioskowanie z niezupełną bazą reguł. Wbrew pozorom, takie wnioskowanie jest możliwe mimo, że brak niektórych reguł może być interpretowany jako częściowy brak wiedzy koniecznej do przekształcenia wejść w wyjścia. Brak tej wiedzy może być kompensowany do pewnego stopnia ze względu na nadmiarowość informacyjną zawartą w zdefiniowanych regułach. Ta obserwacja ma także duże znaczenie praktyczne, ze względu na charakterystyczną dla wnioskowania rozmytego odporność na błędy w regułach.
Wnioskowanie realizowane przez maszynę wnioskującą może być:
- wnioskowaniem opartym na pojedynczej regule lub
- wnioskowaniem opartym na zbiorze (złożeniu) reguł.