Podręcznik: Wnioskowanie oparte na pojedynczej regule

3. Modelowanie rozmyte

3.7. Wnioskowanie oparte na pojedynczej regule

We wnioskowaniu opartym na pojedynczej regule, do oceny stopnia spełnienia wniosku wykorzystuje się zwyczajowo implikację Mamdaniego. Stopień spełnienia wniosku nazywany jest również stopniem aktywacji reguły lub poziomem jej zapłonu. Jak wynika z (82) reguła jest zapisem relacji rozmytej pomiędzy poprzednikiem reguły a jej następnikiem. Rozważmy przykład pojedynczej reguły:

$jeżeli\; (x=N_x)\cap(y=N_y)\; to\; (x= N_{z})$	(103)

W tej regule wyrażenia $(x=N_x)$ i $(y=N_y)$ poprzedzające słowo kluczowe to są poprzednikami reguły, zaś wyrażenie $(z =N_z)$ następujące po słowie to jest następnikiem reguły. Symbole $x$ , $y$ , $z$ są nazwami zmiennych lingwistycznych, a symbole $N_x$ , $N_y$ , $N_z$ są etykietami funkcji przynależności zbiorów rozmytych będących wartościami odpowiednio zmiennych $x$ , $y$ i $z$ .

W procesie rozmywania wejść każda przesłanka przyjmuje wartość ze znormalizowanego zakresu $[0,1]$ .

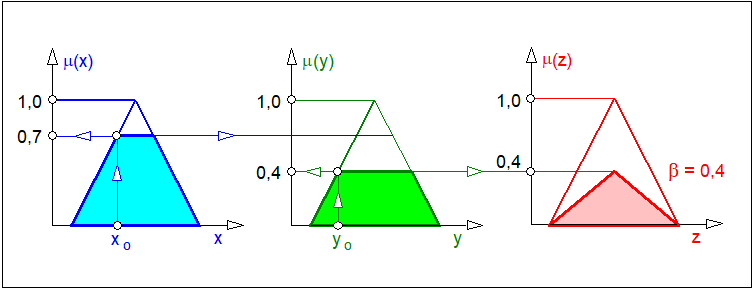
Załóżmy, że w chwili $t_o$ wartości funkcji przynależności $N_x$ i $N_y$ są odpowiednio równe $\mu_{N_x}=0,4$ i $\mu_{N_y}=0,7$ . Postać szczególna reguły (103) na wówczas postać:

$jezeli\; (\mu_{N_x}=0,4)\cap(\mu_{N_y}=0,7)\; to\; (\mu_{N_z}=?)$	(104)

Powstaje pytanie jaką wartość $\mu_{N_z}$ implikuje przesłanka złożona z dwóch przesłanek prostych:

$(\mu_{N_x}=0,4)\cap(\mu_{N_y}=0,7)$	(105)

W istocie jest to pytanie, w jaki sposób z przesłanki złożonej wyprowadzić prawidłowy wniosek, a zatem pytanie o istotę i mechanizm wnioskowania. Jest oczywiste, że odpowiedź na to pytanie ma fundamentalne znaczenie w logice rozmytej.

Wartości funkcji przynależności określają stopień przynależności do zbioru rozmytego. Rozważmy poprzednik reguły (105). Znane są co prawda wartości funkcji przynależności obu przesłanek, natomiast nieznany jest stopień przynależności całego poprzednika. Znajomość tego stopnia jest istotna ponieważ określa stopień spełnienia wniosku wynikającego z tej reguły.

Zwróćmy uwagę, że trudno byłoby przyjąć w naszym przykładzie, że stopień ten wynosi 0,7 ze względu na fakt, że stopień spełnienia drugiej przesłanki wynosi zaledwie 0,4. Stosując racjonalne i ostrożne rozumowanie należy uznać, że stopień spełnienia przesłanki złożonej tej reguły może być co najwyżej równy 0,4 tzn. równy mniejszej z wartości przesłanek prostych. Skoro tak, to należy przyjąć, że w takim samym stopniu spełniony jest następnik reguły. Ponieważ minimalna wartość funkcji przynależności przesłanki prostej wynosi 0,4, to w tym przypadku, mówimy, że reguła odpaliła lub wypaliła na poziomie $\tau =0,4$ . Z formalnego punktu widzenia rozumowanie to dobrze opisuje implikacja Mamdaniego (82).

Należy uznać, że poziom zapłonu reguły wyznacza nieprzekraczalny poziom wartości funkcji przynależności następnika (wniosku). Zatem w naszym przykładzie także wartość $\mu_{N_z}$ nie powinna w chwili $t_o$ przekraczać wartości 0,4. Stąd wynika, że poziom zapłonu reguły ogranicza funkcję przynależności następnika odcinając ją na poziomie zapłonu reguły. Operację tę zilustrowano na rysunku poniżej

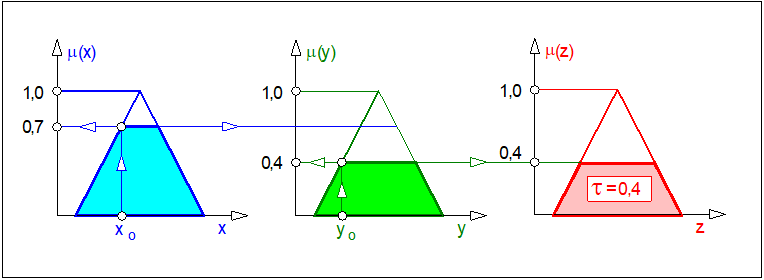
Schemat wnioskowania opartego na wnioskowaniu skalowanym... — Rys. 16. Schemat wnioskowania opartego na implikacji Mamdaniego dla pojedynczej reguły typu: $\textbf{jeżeli} (\mu_{N_x}=0,4)\cap (\mu_{N_y}=0,7) \textbf{to} (\mu_{N_z}= ?)$ . Poziom zapłonu reguły wynosi $\tau = 0,4$ . Odcięcie zbioru rozmytego następnika reguły tworzy ścięty zbiór rozmyty.

Rys. 16. Schemat wnioskowania opartego na implikacji Mamdaniego dla pojedynczej reguły typu: $\textbf{jeżeli} (\mu_{N_x}=0,4)\cap (\mu_{N_y}=0,7) \textbf{to} (\mu_{N_z}= ?)$ . Poziom zapłonu reguły wynosi $\tau = 0,4$ . Odcięcie zbioru rozmytego następnika reguły tworzy ścięty zbiór rozmyty.

Odcięcie zbioru rozmytego następnika może być traktowane jako wyznaczenie wagi reguły.

Wnioskowanie oparte na pojedynczej regule stosowane jest powszechnie w zastosowaniach praktycznych z uwagi na efektywność obliczeniową i niewielkie wymagania na wielkość zasobów pamięciowych.

W literaturze dotyczącej sterowania rozmytego występuje także tak zwane wnioskowanie skalowane. Polega ono wyznaczeniu stopnia spełnienia przesłanek $\beta$ tak jak w implikacji Mamdaniego i przeskalowaniu liniowym zbioru następnika wyznaczonym stopniem $\beta$ . Schemat wnioskowania skalowanego dla pojedynczej reguły podano na rys. 17

$\mu^s(z)=\bigcup_{j=1}^{n}min\left(\mu_j(x_j)\cdot \mu(z)\right)\quad;\quad\forall x_j\in X_j$	(106)

gdzie:

$\mu_j(x_j)$ - funkcja przynależności j-tego zbioru rozmytego przesłanki złożonej,
$\mu (z)$ - funkcja przynależności zbioru rozmytego następnika,
$\mu^s(z)$ - funkcja przynależności przeskalowanego zbioru rozmytego następnika.