Podręcznik
Wstęp do logiki rozmytej
3. Modelowanie rozmyte
3.8. Wnioskowanie oparte na zbiorze reguł
Powyżej rozpatrywaliśmy wnioskowanie oparte na pojedynczej regule. W praktycznych zadaniach mamy do czynienia zwykle nie z pojedynczą regułą, ale zbiorem reguł. Zastosowanie wnioskowania opartego na pojedynczej regule dla każdej reguły z tego zbioru generuje zbiór wniosków cząstkowych. Pojawia się pytanie w jaki sposób można wyprowadzić wniosek końcowy w takim przypadku?
Rozumowanie może być następujące: Jeśli uznamy, że wnioski cząstkowe wyprowadzone na podstawie ostrożnej ewaluacji pojedynczych reguł są racjonalne, to racjonalna jest też suma mnogościowa tych wniosków. Jeśli zatem wnioski cząstkowe tworzone były zgodnie z zasadą minimum to wnioskowanie oparte na zbiorze reguł może być traktowane jako operacja sumy mnogościowej wniosków z pojedynczych reguł. Formalnie ten sposób wnioskowania możemy zapisać w postaci:
| \( \mu(y)=\bigcup_{i=1}^{n}\mu_i(y)\cap \tau_i \) | (107) |
|---|
gdzie: \( \mu (y) \) – funkcja przynależności zagregowanego wniosku ze zbioru reguł,
\( \mu_i(y)\cap \tau_i \) – obcięta funkcja przynależności wniosku z i-tej reguły.
Wnioskowanie oparte na zbiorze reguł
Załóżmy, że mechanizm wnioskowania opartego na zbiorze reguł wykorzystamy do wyznaczenia wyjścia rozmytego regulatora typu P z jednym wejściem i jednym wyjściem. Wielkością wejściową regulatora jest odchyłka regulacji \( e \), wielkością wyjściową regulatora jest wartość nastawiająca (sterująca) \( y \). Załóżmy dalej, że dokonano rozmycia wejścia \( e \) i wyjścia \( y \) w taki sposób, że zmiennej lingwistycznej < odchyłka regulacji > przyporządkowano trzy wartości < ujemna >, < zerowa >, < dodatnia > i podobnie zmiennej lingwistycznej < sterowanie > przyporządkowano wartości < zmniejsz >, < bez zmian >, < zwiększ >. Etykietom < ujemna >, < zerowa >, < dodatnia > przyporządkowano dla uproszczenia odpowiednio symbole \( N_e \),\( Z_e \), \( P_e \). Podobnie etykietom < zmniejsz >, < bez zmian >, < zwiększ > przyporządkowano symbole \( N_y \),\( Z_y \), \( P_y \). Założono kształt funkcji przynależności jak na Rys. 18. Opierając się na wiedzy heurystycznej skonstruowano tabelę sterowań rozmytych jak poniżej.
| Reguła | \( e \) | \( y \) |
|---|---|---|
| 1 | \( N_e \) | \( N_y \) |
| 2 | \( Z_e \) | \( Z_y \) |
| 3 | \( P_e \) | \( P_y \) |
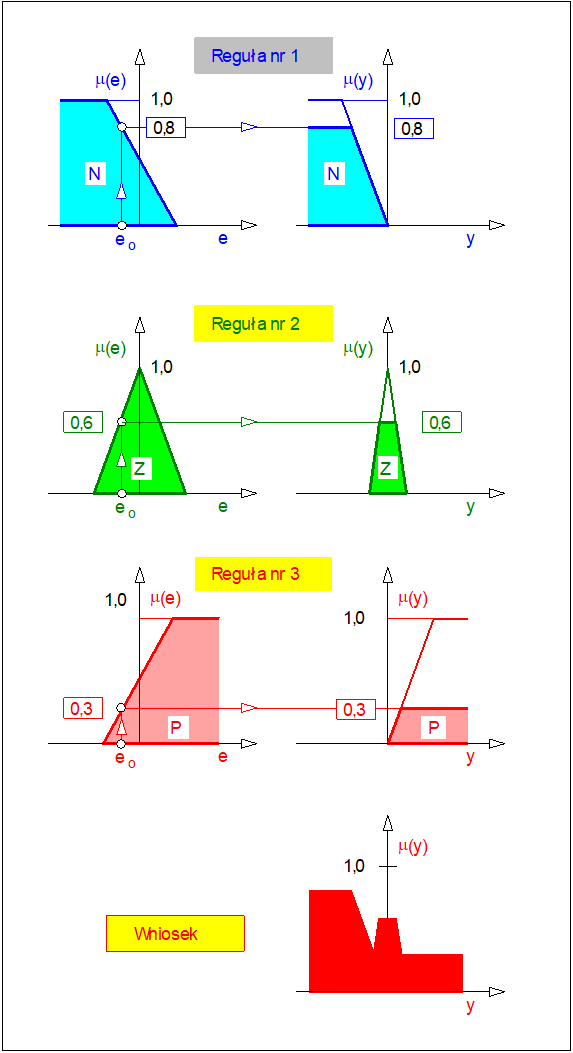
Schemat sposobu wyznaczenia wniosku ze zbioru reguł opisujących rozmyty regulator typu P przedstawiono na rysunku poniżej. Jak łatwo zauważyć zagregowany wniosek ma charakter rozmyty. Z punktu widzenia praktycznego, poza nielicznymi wyjątkami, wniosek taki nie jest przydatny. Konieczne jest zatem przekształcenie wniosku rozmytego do postaci ostrej akceptowalnej w świecie realnym. Należy zwrócić uwagę na stratność takiego przekształcenia wynikająca z faktu przekształcenia obiektu dwuwymiarowego do obiektu zerowymiarowego tj. numerycznej wartości ostrej.