Podręcznik

Metoda środka ciężkości (COG) zwaną czasami metodą środka obszaru (COA) jest najbardziej popularną metodą wyostrzania. Istota tej metody polega na następującym rozumowaniu.

Funkcja przynależności zagregowanego wniosku rozmytego zakreśla pewien obszar na dwuwymiarowej półpłaszczyźnie wyznaczonej przez osie przestrzeni rozważań wyjścia ostrego i funkcji przynależności (por. Rys. 18). Obszar ten jest ograniczony od góry funkcją przynależności wniosku rozmytego, a od dołu przestrzenią rozważań ostrego wyniku wniosku. Redukcja dwuwymiarowego wniosku rozmytego do wniosku zerowymiarowego wymaga zatem ekstrakcji z tego obszaru podstawowej cechy reprezentowanej przez ten wniosek. Racjonalnym rozwiązaniem jest próba wyważenia wniosku rozmytego. Powstaje jednak pytanie, w jaki sposób można wyważyć wniosek i na czym on polega

Zgodnie z Def. 17, zadanie wyostrzania sprowadza się do rzutowania na oś przestrzeni rozważań wyjścia pewnego punktu charakterystycznego reprezentującego wniosek. W przypadku metody środka ciężkości zaproponowano, aby tym punktem był środek ciężkości obszaru wniosku rozmytego, a reprezentacją ostrą wniosku rozmytego była odcięta tego punktu. W ogólnym przypadku sprowadza się to do wyznaczenia ostrej wartości wniosku \( y^* \) z formuły:

W przypadku, gdy funkcja przynależności wyjścia ma kształt linii poligonowej o \( m \) odcinkach i \( (m+1) \) węzłach (jak np. na Rys. 19) i znane są wszystkie współrzędne węzłów tej linii \( [y_k,\mu_k] \), to środek ciężkości obszaru pod tą linią może być wyznaczony z formuły:

Wyostrzanie zbioru rozmytego

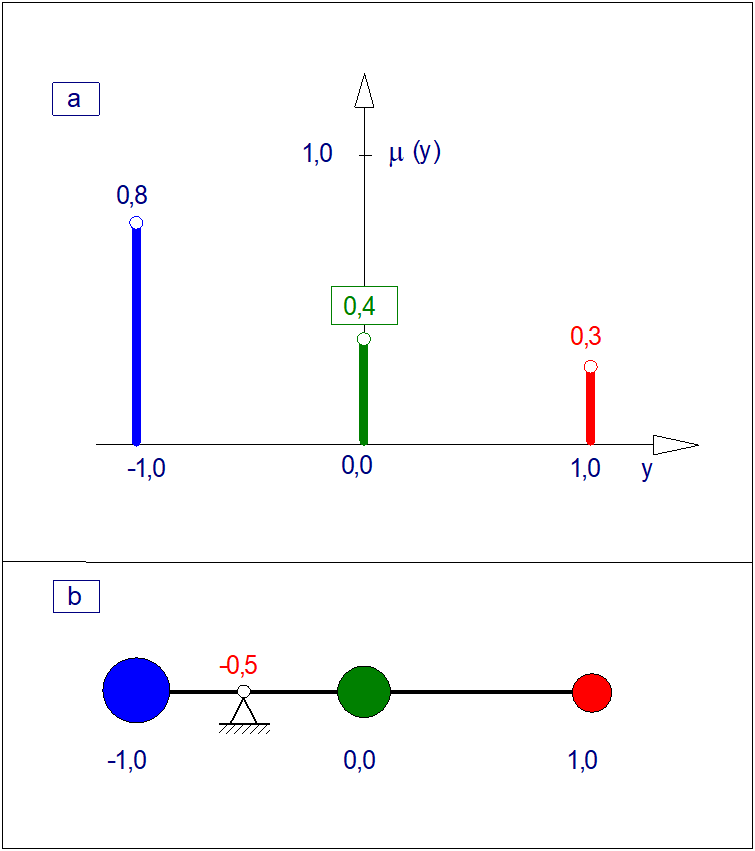
Załóżmy, że funkcje przynależności wszystkich rozmytych wniosków cząstkowych mają postać singletonów czyli zbiorów jednoelementowych jak pokazano na Rys. 20. Ta szczególna postać zbioru rozmytego jest niezwykle ważna z praktycznego punktu widzenia. Pozwala ona bowiem na wyostrzanie wniosku metodą środka ciężkości przy minimalnym nakładzie mocy obliczeniowych.

Ponieważ powierzchnia obszaru pod singletonem jest równa zeru, to bezpośrednie zastosowanie formuły (109) jest niemożliwe. W tym przypadku o wadze każdego wniosku cząstkowego decyduje wysokość i lokalizacja poszczególnych singletonów. W tym przypadku wyznaczenie odciętej punktu ciężkości można sprowadzić do zadania zastępczego polegającego na poszukiwaniu punktu podparcia nieważkiej dźwigni obciążonej masami o wartościach liczbowych równych wysokościom (stopniom aktywacji) singletonów (co zilustrowano na Rys. 20 b). W tym przypadku ważoną wartość ostrą wniosku można wyznaczyć ze zależności:

\( y^*=\frac{\sum_{i=0}^{n-1}y_i\cdot \mu_i}{\sum_{k=0}^{n-1}\mu_i } \)	(111)

Z formuły (111) możemy wywnioskować, że ważoną wartość ostrą określa stosunek sumy pierwszych momentów wysokości singletonów do mocy zbioru rozmytego \( y \).

Niech: \( n=3 \); \( \mu_1 (-1)=0,8 \); \( \mu_2 (0)=0,4 \); \( \mu_3 (1)=0,3 \). Stąd:

\( y^*=\frac{(-1)\cdot 0,8+(0)\cdot 0,4+(+1)\cdot 0,3}{0,8+0,4+0,3}=-\frac{0,5}{1,5}=-\frac{1}{3} \)	(112)