Podręcznik

Jeśli przyjąć założenie, że wysokość zbioru rozmytego jest w jakimś stopniu przybliżoną miarą jego obszaru, to wyobrażalne jest wykonanie operacji wyostrzania zmodyfikowanymi metodami COG lub COS w taki sposób, że przybliżone położenie odciętej środka ciężkości obszaru będzie wyznaczone przez substytucję obszarów przez wysokości zbiorów rozmytych wniosków cząstkowych. Redukcja wymiarowości pozwala na znaczne uproszczenie sposobu wyznaczania wartości ostrej, a tym samym istotnie zmniejsza zapotrzebowanie na moce obliczeniowe.

Do realizacji metody HM potrzebna jest jedynie znajomość współrzędnych wysokości zbiorów rozmytych wniosków cząstkowych. W ten sposób z procesu wyostrzania wyeliminowano kłopotliwe rachunkowo operacje związane z wyznaczaniem zerowych i pierwszych momentów funkcji przynależności wniosków jak w metodach obszarowych COG, COS i COLA.

W przypadku, gdy odcięta wysokości zbioru nie jest jednoznaczna (np. dla zbiorów typu $\Pi$ o trapezowej funkcji przynależności) to w metodzie HM wyznacza się ją jako średnią arytmetyczną jej odciętych prawo- i lewobrzeżnych. Metoda HM sprowadza zatem problem wyostrzania do realizacji metody COG z funkcjami singletonowymi. Możliwe jest zatem w tym przypadku zastosowanie wzoru (111) z zastrzeżeniem, że w miejsce $\mu_i$ podstawimy uśrednioną wysokość wniosku rozmytego z i-tej reguły $h_i$, zaś w miejsce $y_i$ zostanie podstawiona odcięta uśrednionej wartości tej wysokości. Stąd:

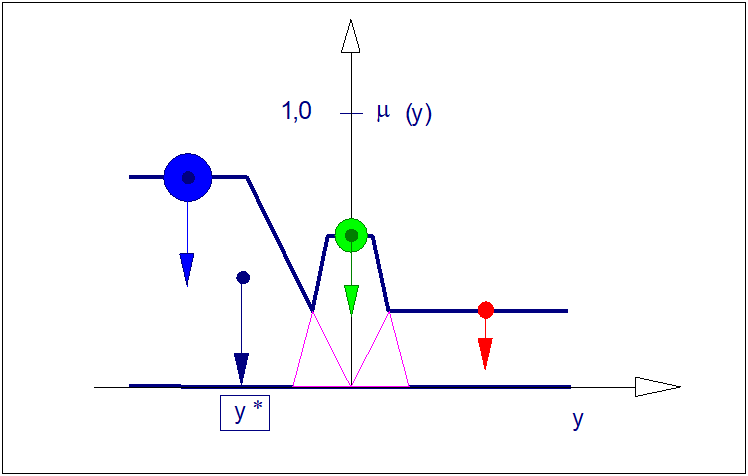
Ilustrację sposobu wyostrzania (defuzyfikacji) metoda HM przedstawiono na rysunku poniżej.