Podręcznik
Wstęp do logiki rozmytej
4. Przykłady regulatorów rozmytych
4.2. Rozmyty regulator dwustawny
W poprzednim rozdziale stwierdziliśmy, że dla rozpatrywanego w nim przypadku, wzmocnienie regulatora rozmytego typu P jest wprost proporcjonalne do różnicy pochodnych liniowych funkcji przynależności wartości wejścia. Zwiększenie nachylenia tych funkcji skutkuje wzrostem wzmocnienia. Jeśli pochodne osiągną wartości teoretycznie nieskończenie wielkie, to wzmocnienie regulatora osiągnie także osiągnie taką wartość. W takim przypadku uzyskujemy przełączającą funkcję sterowania właściwą regulatorom dwustawnym (Rys. 32).
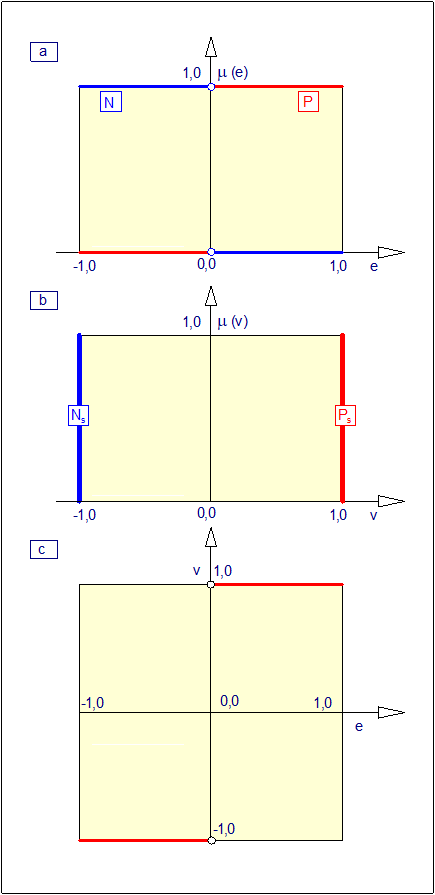
, to wszystkie funkcje przynależności definiują jednocześnie zbiory ostre.a) Funkcje przynależności wejścia
b) Funkcje przynależności wyjścia
c) Funkcja sterowania