Podręcznik: Układ antypoślizgowy ASR

6. Przykłady zastosowań logiki rozmytej

6.4. Układ antypoślizgowy ASR

Źródło: Hiller M., Schmitz T., Schuster C.: Design of a Fuzzy Traction Control System Using Spatial Vehicle Dynamics Simulation, International Workshop on Fuzzy Technologies in Automation and Intelligent Systems, Fuzzy Duisburg '94, s. 117..126, Uniwersytet w Duisburgu, 1994.

Nadmierne przyśpieszenie pojazdu w warunkach nierównomiernych właściwości ciernych powierzchni jezdni prowadzić może do utraty sterowalności pojazdu ze względu na powstanie niekontrolowanych składowych sił tarcia w kierunku jazdy. Pojazdy o napędzie na przednie koła tracą sterowność, natomiast pojazdy o napędzie na tylne koła zachowują się w sposób nieprzewidywalny.

Systemy ASR są systemami sterowania automatycznego pozwalającymi na ograniczenie współczynnika poślizgu kół do poziomu zapewniającego osiągnięcie właściwych parametrów trakcyjnych pojazdu.

Ograniczenie współczynnika poślizgu wiąże się z aktywnym oddziaływaniem na charakterystyki trakcyjne pojazdu. Istnieją w zasadzie dwa sposoby sterowania właściwościami trakcyjnymi pojazdu. Z jednej strony możliwe jest zmniejszenie momentu obrotowego silnika przez dławienie dopływu mieszanki paliwowo-powietrznej i odpowiednie oddziaływanie na układ zapłonu silnika, z drugiej zaś strony moment napędowy każdego z kół może być ograniczony np. przez odpowiednio kontrolowane hamowanie kół. Obydwie metody w różnym stopniu stosowane są we współczesnych układach ASR. W zakresie niewielkich prędkości pojazdu nadmierne dławienie dopływu mieszanki paliwowej do silnika jest niemożliwe ze względu na potencjalną możliwość zadławienia silnika, w zakresie zaś większych prędkości stosowanie metody ograniczania momentu napędowego przez hamowanie prowadziłoby do zbyt dużego zużycia okładzin hamulcowych i opon kół bieżnych.

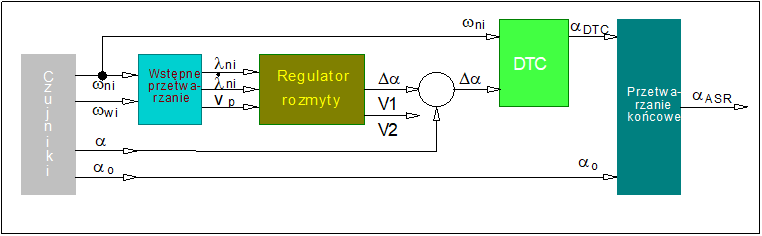
Rys. 49. Schemat ogólny rozmytego regulatora momentu napędowego w układzie ASR. Oznaczenia: $\omega_{ni}$ - prędkość kątowa i-tego koła napędowego, $\omega_{wi}$ - prędkość kątowa i-tego koła wolnego, DTC - układ sterowania momentu obrotowego, $\lambda_{ni}$ - współczynnik poślizgu kątowa i-tego koła napędowego, $\lambda_{wi}$ - współczynnik poślizgu kątowa i-tego koła wolnego, $v_p$ - średnia prędkość obwodowa kół wolnych, $\alpha$ - kąt pedału przyśpieszenia, $\alpha_0$ - kąt otwarcia przepustnicy, $\Delta \alpha$ - zmiana sterowania kąta otwarcia przepustnicy, $V1$ , $V2$ - sygnały sterujące elektromagnesów rozdzielaczy układów hamulcowych kół.

Na podstawie pomiaru prędkości obrotowej kół napędowych i kół ciągnionych (wolnych) ( $\omega_{ni}$ , $\omega_{wi}$ ) w układzie wstępnego przetwarzania danych (Rys. 49) następuje wyznaczenie współczynników poślizgów $\lambda_{ni}$ kół napędowych, $\lambda_{wi}$ kół wolnych oraz średniej prędkości obwodowej kół wolnych $v_p$ .

$v_p =0,5\cdot r_r\left(\omega_{w1}+\omega_{w2} \right)$	(173)

gdzie: $r_r$ - promień dynamiczny koła, $\omega_{w1}, \omega_{w2}$ – prędkości kątowe pierwszego i drugiego koła wolnego.

Współczynnik poślizgu $\lambda_{ni}$ każdego z kół napędowych (i=1, 2) wynosi:

$\lambda_{ni} =1-\frac{\omega_{wi}}{\omega_{ni}}\quad ;\quad v_p\neq0$	(174)

Pochodną współczynnika poślizgu względem czasu można przybliżyć stosunkiem przyrostu współczynnika poślizgu do czasu, w którym on występuje:

$\frac{d\lambda_{ni}}{dt}\approx\frac{\lambda_{ni}(t)-\lambda_{ni}(t-\Delta t)}{\Delta t}$	(175)

gdzie: $\Delta t$ - okres impulsowania regulatora.

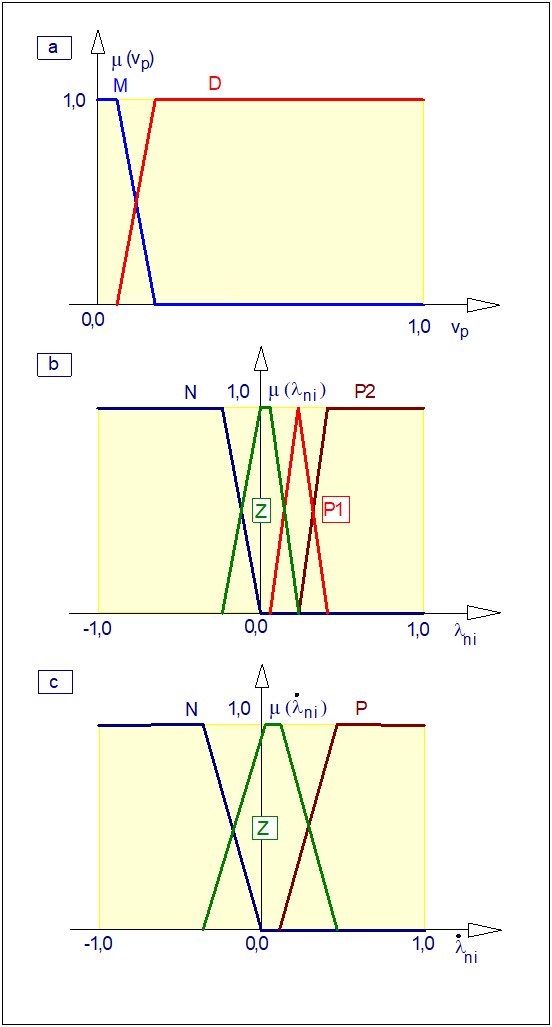
Rys. 50. Funkcje przynależności wejść regulatora układu ASR.

Wielkości $v_p$ , $\lambda_{ni}$ i $\frac{d\lambda_{ni}}{dt}$ są wejściami regulatora rozmytego. Na Rys. 50. przedstawiono funkcje przynależności tych wejść. Prędkości średniej pojazdu przyporządkowano dwie wartości: <mała> i <duża>, współczynnikowi poślizgu *ni przyporządkowano cztery wartości: <ujemny>, <zerowy>, <niewielki dodatni> i <duży dodatni>, prędkości współczynnika poślizgu $\frac{d\lambda_{ni}}{dt}$ przyporządkowano trzy wartości: <ujemny>, <zerowy> i <dodatni>.

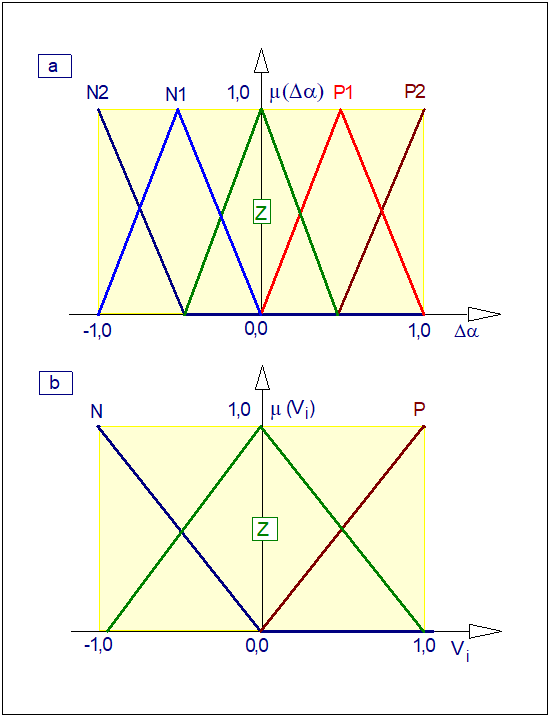
Wyjściami regulatora rozmytego są: sygnał zmiany położenia kątowego przepustnicy $\Delta \alpha$ oraz wartości sterowań rozdzielaczy elektrohydraulicznych o działaniu proporcjonalnym w układach hamulcowych kół napędzających $V1$ i wolnych $V2$ . Na Rys. 51. przedstawiono funkcje przynależności wyjść regulatora rozmytego. Zmianie kąta przepustnicy $\Delta \alpha$ przyporządkowano pięć wartości: <ujemny duży>, <ujemny mały>, <bez zmian>, <dodatni mały> i <dodatni duży> sygnałom sterującym $V1$ i $V2$ przyporządkowano po trzy wartości: <zmniejsz sterowanie>, <sterowanie bez zmian> i <zwiększ sterowanie>.

Tabela 17: Tabela sterowań rozmytych regulatora momentu hamującego.
Regulator rozmyty układ ASR		$\lambda_{ni}$
Regulator rozmyty układ ASR		$P2$	$P1$	$Z$	$N$
$\Delta \lambda_{ni}$	$P$	$P$	$P$	$Z$	$N$
	$Z$	$P$	$P$	$N$	$N$
	$N$	$P$	$Z$	$N$	$N$

Tabela 18: Tabela sterowań rozmytych regulatora momentu obrotowego silnika spalinowego.
Regulator rozmyty układ ASR		$\lambda_{ni}$
Regulator rozmyty układ ASR		$P2$	$P1$	$Z$	$N$
$\Delta \lambda_{ni}$	$P$	$N2$	$N2$	$Z$	$Z$
	$Z$	$N2$	$N1$	$P2$	$N1$
	$N$	$N1$	$Z$	$P1$	$N2$

W maszynie wnioskującej zastosowano schemat wnioskowania Mamdaniego. Oprócz regulatora rozmytego system sterowania trakcyjnego zawiera układ DTC oraz układ końcowego przetwarzania danych. Układ DTC zabezpiecza przepustnicę przed całkowitym zamknięciem, tak aby nie dopuścić do zatrzymania silnika. Końcowy układ przetwarzania danych spełnia rolę komparatora porównującego położenie kątowe przepustnicy (sygnał wyjściowy z regulatora rozmytego ASR) z sygnałem tempomatu w celu ewentualnej korekcji położenia kątowego przepustnicy.

Rys. 51. Funkcje przynależności wyjść regulatora rozmytego układu ASR.

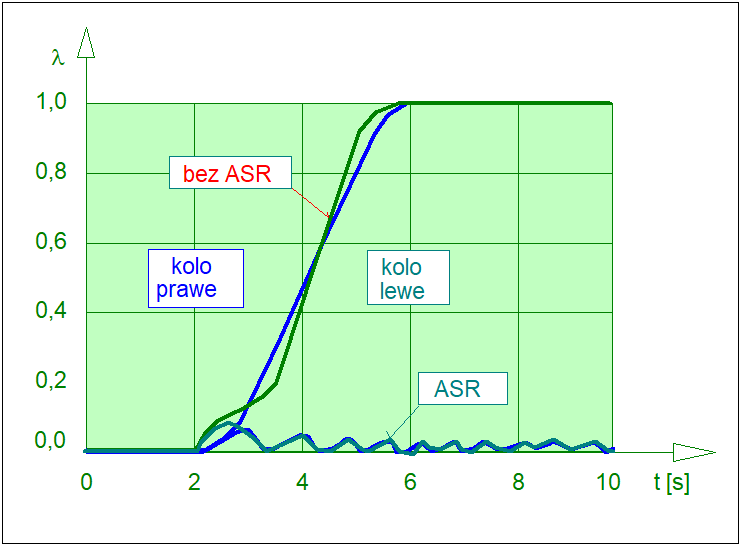
Wyniki symulacji pracy układu dla samochodu Mercedes-Benz W140 przedstawiono na Rys. 52.

Przykład ten wskazuje na walory aplikacyjne regulatorów rozmytych zwłaszcza w warunkach gdy nie jest znany model analityczny obiektu regulacji. Przykład wskazuje również, że do syntezy układów regulacji może być użyta z powodzeniem jakościowa wiedza heurystyczna.

Przykładowy przebieg współczynnika poślizgu kół na oblodzonej jezdni — Rys. 52. Przykładowy przebieg współczynnika poślizgu kół $\lambda$ na oblodzonej jezdni.

Rys. 52. Przykładowy przebieg współczynnika poślizgu kół $\lambda$ na oblodzonej jezdni.