1. Wprowadzenie.

Podstawowe informacje

Klasą zadań, dla których najwcześniej podano algorytm prosty i skuteczny (i w zasadzie do dzisiaj najlepszy) są zadania liniowe optymalizacji. Zajmiemy się teraz krótko tymi zadaniami. 

Zapisując te zadania i przedstawiając ich podstawowe własności będziemy posługiwać się notacją wektorowo macierzową, w której duże litery, np. A, oznaczają macierze, małe litery np. b, to w zasadzie wektory kolumnowe, małe litery z indeksami, np. xi oraz litery greckie to liczby, a znak T oznacza transpozycję.

Określmy formalnie przedmiot rozważań tego modułu.

Zadanie programowania liniowego (zadanie liniowe optymalizacji, zadanie PLin)
znaleźć  \(w^o=\mathrm{argmin}_{w\in D}z^T  w\)
gdzie: \(z\in \mathbb{R}^q\)  jest danym wektorem (często zwanym wektorem cen),
\(D=\left\{ w \in\mathbb{R}^q| (\forall j\in \overline{1,m})a_j^Tw\leq\beta _j\wedge (\forall k\in \overline1,\tilde{p})a_k^Tw=\beta _j\wedge (\forall i \in \overline{1,n})w_i \geq0\right\}.\)
Jest to tak zwana postać ogólna zadania programowania liniowego (linear programming problem).

Funkcja oceny jest tu liniowa, a nie afiniczna, bo jest oczywiste, że dodanie do niej dowolnej liczby nie zmienia rozważań (zmienia wartość funkcji wyboru w punkcie minimalizującym, która jest oczywiście od tej liczby zależna, ale rozwiązaniem zadania jest punkt minimalizujący, który się nie zmienia!).

Wprowadzenie

Narysujmy zbiór dopuszczalny i wykres poziomicowy funkcji wyboru dla prostego zadania liniowego (zapiszemy go w trochę inny sposób niż dotychczas, aby oswoić się z różnymi wariantami zapisu stosowanymi w literaturze).

      \(f(x,y)=50x+100y →\mathrm{max}_{(x,y)}\)

przy ograniczeniach (p.o.) 

\(10x + 5y \leq 2 500\)   (a)

\(4x + 10y \leq 2 000\)   (b)

\(x + 1.5y \leq 450 \)     (c)

\(x \geq 0, \, y \geq 0.  \)

 

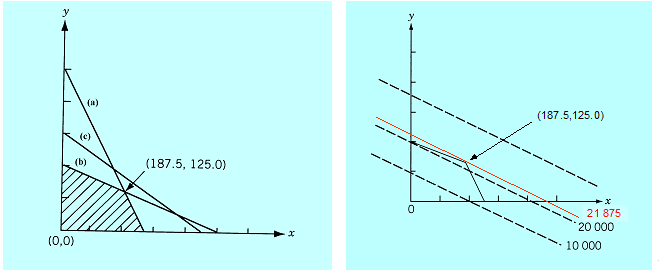
Rys. 2.1: Proste zadanie programowania liniowego

Z rysunku wynika, że ograniczenie (c) nie jest potrzebne, oraz że zbiór dopuszczalny jest wielokątem Linie poziomicowe funkcji liniowej to proste, zatem rozwiązanie leży w wierzchołku wielokąta (albo rozwiązań jest wiele i leżą na brzegu wielokąta, gdy poziomice są równoległe do stosownego ograniczenia).

Te wnioski można uogólnić na dowolne zadanie liniowe. Trzeba tylko wielokąt zastąpić wielościanem, a prostą – płaszczyzną. Zatem:

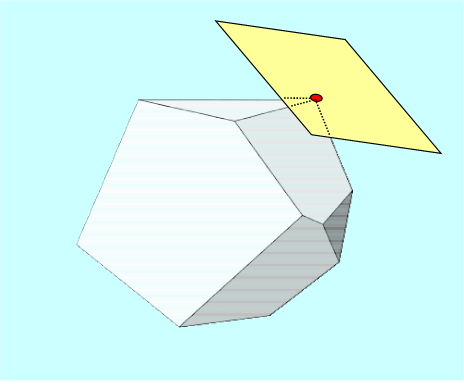
W przestrzeni zmiennych liniowego zadania optymalizacji miejscem geometrycznym stałej wartości funkcji celu jest (hiper)płaszczyzna, zbiór dopuszczalny to (hiper)wielościan, a rozwiązanie zadania (o ile istnieje) leży w jego wierzchołku albo rozwiązań jest wiele i leżą na krawędzi wielościanu albo na jego ścianie.

 

Rys. 2.2: Zbiór dopuszczalny i płaszczyzna stałej wartości funkcji celu (poziomica) zadania programowania liniowego o trzech zmiennych.

Wróćmy do naszego opowiadania o Algorytmie. Przyjmijmy, że przekazaliśmy mu powyższą wiedzę. Co Algorytm może wymyślić? Odpowiedź jest oczywista:

Musi znaleźć jakiś wierzchołek, 

potem sprawdzić jego sąsiadów (dla minimalizacji, sprawdzić czy funkcja celu maleje), 

wybrać najkorzystniejszy, i procedurę powtórzyć.

 

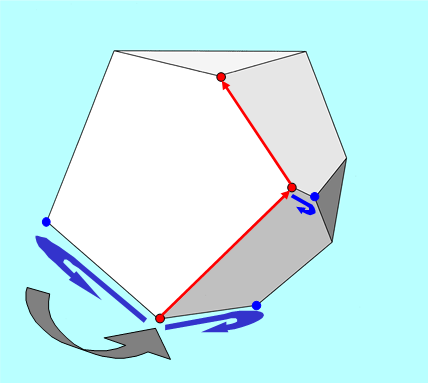
Rys. 2.3: Algorytm rozwiązywania zadania programowania liniowego

Na płaszczyźnie taki algorytm będzie działać, bo każdy wierzchołek ma tylko dwu sąsiadów, ale przy większej liczbie wymiarów będzie to bardzo powolne i nie wiadomo, czy algorytm się nie zapętli.

Pierwsze zadania optymalizacji, które obecnie zaliczamy do zadań liniowych sformułowano pod koniec lat trzydziestych XX w. (matematycy J. von Neumann z Princeton i L. Kantorowicz, wtedy z Leningradu). Różne zadania związane z optymalnym przydziałem zasobów sformułowano na potrzeby armii amerykańskiej w czasie drugiej wojny światowej. Wtedy też zaczęto intensywne prace nad opracowaniem metod pozwalających na znalezienie rozwiązań, jak wtedy zaczęto mówić, zadań programowania liniowego. W roku 1947 G.B. Dantzig opublikował swój algorytm znajdowania rozwiązania zadania liniowego optymalizacji. Nazwał go metodą SIMPLEX. W Polsce, nie bardzo wiadomo dlaczego, algorytm Dantziga nazywa się metodą sympleks, simpleksową, a nawet metodą sympleksów. 

Nie będziemy szczegółowo prezentowali tego algorytmu, odsyłając Czytelnika do literatury (np. podręczników: A. Stachurski: Wprowadzenie do optymalizacji, Oficyna Wydawnicza PW 2009, rozdział 2, lub W. Findeisen, J. Szymanowski, A. Wierzbicki: Teoria i metody obliczeniowe optymalizacji, PWN 1977 (część I rozdział 4)). Przedstawimy tylko główną ideę jego działania.

Ponieważ w metodzie Simplex wykorzystuje się pojęcia i metody, które powstały dla rozwiązywania układu równań liniowych, pierwszą czynnością jaką trzeba wykonać jest przekształcenie otrzymanego zadania liniowego do tzw. postaci kanonicznej (standardowej). Zbiór dopuszczalny w postaci kanonicznej jest określony tylko przez ograniczenia równościowe i ograniczenia znaku.

Zadanie liniowe optymalizacji w postaci kanonicznej (zadanie liniowe optymalizacji, zadanie PLin_K)
\(c^Tx \to\mathrm{min}\)
p.o. \( (∀j∈\overline{(1,p)}) a_j^T x=β_j  oraz (∀i∈\overline{1,n}) x_i≥0.\)
W powyższym sformułowaniu zakłada się, że \(p < n \)
oraz przyjmuje się, że \(x,c,a_j∈\mathbb{R}^n\) oraz \((∀j∈\overline{1,p}) β_j≥0.\)

Jeżeli oznaczymy

\(A=\begin{bmatrix}a_1^T \\\vdots \\a_p^T \end{bmatrix},\,\mathrm{oraz}\,b=\begin{bmatrix}\beta _1^T \\\vdots \\\beta _p^T\end{bmatrix},\)

a także przyjmiemy skrócony zapis \(x \geq 0\) na ograniczenia znaku, to określenie zbioru dopuszczalnego zadania w postaci kanonicznej możemy zapisać następująco

\(DK={x∈\mathbb{R}^n |x≥0∧Ax=b},  \,b≥0. \qquad (2.1)\)

Każdy wektor \( x \in DK \) nazywamy wektorem dopuszczalnym (zadania optymalizacji).

Pokażemy teraz jak przejść z postaci ogólnej do kanonicznej.

  • Ograniczenia nierównościowe przekształcamy wprowadzając zmienne dopełniające \(x_q+j\)

     \([a_j^T w≤β_j∧w∈\mathbb{R}^q]⇔[a_j^T w+x_(q+j)=β_j∧x_(q+j)≥0].\)

  • Nie w każdym zadaniu PLin konieczne jest ograniczenie znaku zmiennych. Ponieważ zmienne zadania w postaci kanonicznej muszą mieć ograniczony znak, to warunek ten spełnia się przez następujące podwojenie zmiennych:

     \(w_i∈ \mathbb{R}⇔(w_i=x_i^+-x_i^-∧x_i^+≥0∧x_i^-≥0).\)

Przejście od postaci ogólnej do kanonicznej zadania programowania liniowego
Zadanie PLin jest następujące: 
znaleźć  \(w^o=[w_1^o,w_2^o]^T=\mathrm{argmin}_{w∈D}⁡(z^T  x= [5\,⋮-7]\begin{bmatrix}w_1\\w_2 \end{bmatrix}\)
gdzie: \(D={w∈\mathbb{R}^2 |3w_1-5w_2≤15∧2w_1+4w_2≤18∧ w_1≤0}.\)
Najpierw przekształcimy równoważnie nierówności w równości:
\(3w_1-5w_2≤15   ⇔  3w_1-5w_2+w_3=15∧w_3≥0 \)
\(2w_1+4w_2≤18  ⇔ 2w_1+4w_2+w_4=18∧w_4≥0.\)
Zmienna \(w_2\)jest „wolna” – nie ma ograniczenia znaku, a definicja zadania PLin_K taką sytuację wyklucza. Wobec tego musimy dokonać jej przekształcenia na różnicę dwu zmiennych nieujemnych. Wprowadźmy zatem dwie zmienne  \(w_5 ≥0 \) oraz \(w_6≥0\) i dodajmy równanie \(w_2=w_5 -w_6.\)
Trzeba jeszcze „poprawić” ograniczenie znaku podstawiając \(w_1=-w_7.\)

Zbiór DK zadania PLin_K  o tym samym rozwiązaniu co zadanie wyjściowe jest więc równy
\(DK=w∈\mathbb{R}^5 |3(w_1=-w_7)-5(w_2=w_5 -w_6) + w_3=15∧w_3≥0∧w_5 ≥0 ∧ w_6≥0∧ \)
\(∧2(w_1=-w_7)+4(w_(2 ) =w_5 -w_6)+ w_4=18∧w_4≥0∧(w_1=-w_7)≤0=\)
\(=w∈\mathbb{R}^5 | w_3-5w_5+5w_6  〖-3w〗_7=15∧w_4+4w_5 -4w_6  -2w_7=18\)
\(∧w_3≥0∧w_4≥0∧w_5 ≥0 ∧ w_6≥0∧w_7≥0,\)
a jego funkcja celu jest następującym iloczynem skalarnym: \([0\,⋮\,0\,⋮-7\,⋮\,7\,⋮-5]\begin{bmatrix}w_3\\w_4\\w_5\\w_6\\w_7 \end{bmatrix}\).
Zmieniając nazwę zmiennych (na x) i w naturalny sposób numery zmiennych \((x_i=w_{i+2})\) otrzymujemy standardowy zapis zadania PLin_K
znaleźć  \(x^o=[x_1^o,...,x_5^o]^T=\mathrm{argmin}_{x∈DK)}(c^T  x= [0\,⋮\,0\,⋮\,-7\,⋮\,7\,⋮\,-5]\begin{bmatrix}x_1\\x_2\\x_3\\x_4\\x_5 \end{bmatrix}\)
gdzie:  \({DK=x∈\mathbb{R}^5 |x_1-5x_3+5x_4-3x_5=15∧x_2+4x_3-4x_4-2x_5=18∧ (∀i∈\overline{1,5} x_i≥0.}\)

Omówimy teraz podstawowe zasady konstrukcji algorytmu Simplex.