1. Pytania i zadania kontrolne dla Modułu 3

1. Podać, wraz z uzasadnieniem, co najmniej dwa przykłady funkcji ściśle wypukłej nie mającej minimum.


2. Czy ze ścisłej wypukłości funkcji klasy \(\mathbf{C}^2\) wynika dodatnia określoność jej macierzy Hessego.


3. Zbadać wypukłość następujących funkcji

\(\mathbb{R}∍x↦f(x)= |x|+x^2∈\mathbb{R}\)

\(\mathbb{R}∍x↦f(x)=\mathrm{exp}⁡\dfrac{-1}{2} x)+x^4∈\mathbb{R}.\)


4. Zmierzoną zależność między dwoma wielkościami x i I opisuje następująca tabela

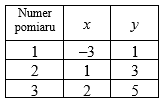
Jako model zależności pomiędzy mierzonymi wielkościami przyjęto zależność afiniczną:  \(y = \alpha x + \beta\),

a za kryterium wyboru wartości parametrów \(\alpha\) i \(\beta\) przyjęto sumę kwadratów różnic między zmierzonymi wartościami zmiennej y a wartościami wynikającymi z wybranego modelu dla tych samych wartości zmiennej x. 

Sformułować zadanie optymalizacji doboru parametrów modelu metodą najmniejszych kwadratów (patrz punkt 1.2.3). 

Wyznaczyć te parametry posługują się Procedurą redukcji ZOBO do układu równań omówioną w punkcie 3.1.1.

Wykonać (może być szkicowy) rysunek poziomic funkcji minimalizowanej.


5. Ustalić wypukłość albo wklęsłość funkcji  \(\mathbb{R}^2∍x↦f(x)= x^T Qx+c^T x∈\mathbb{R}\)

jeżeli \( Q=\begin{bmatrix}3&1\\2&4\\\end{bmatrix},\, Q=\begin{bmatrix}-3&1\\2&-4\\\end{bmatrix},\, Q=\begin{bmatrix}6&2\\1&-2\\\end{bmatrix}, \,Q=\begin{bmatrix}3&2\\0&2\\\end{bmatrix}\)


6. Dla funkcji \(\mathbb{R}^2∍x↦f(x)= (x_1 )^2+x_1 x_2+3(x_2 )^2∈\mathbb{R}\) obliczyć wzory określające: gradient, pochodną kierunkową w kierunkach  \(d = (1, 1)\) oraz \(p = (–1, 1)\), a także macierz Hessego.


7. Znaleźć aproksymację kwadratową, wg. wzoru (3.3), funkcji

 \((x_1,x_2)\mapsto f(x_1,x_2)=(x_1-1)^2\mathrm{exp}(x_2)+x_1\)

w punktach (0,0) oraz (1,1).


9. Przedstawić podstawowe zasady konstruowania algorytmów optymalizacji.


10. Przedstawić podobieństwa i różnice między zadaniami ZPK i ZKK.