Podręcznik
| Strona: | SEZAM - System Edukacyjnych Zasobów Akademickich i Multimedialnych |
| Kurs: | Analiza symboliczna obwodów w stanie ustalonym |
| Książka: | Podręcznik |
| Wydrukowane przez użytkownika: | Gość |
| Data: | wtorek, 27 stycznia 2026, 23:18 |
Spis treści
- 1. Podstawowe pojęcia i prawa obwodów elektrycznych
- 1.1. Podstawowe pojęcia obwodów
- 1.2. Podstawowe elementy obwodu elektrycznego
- 1.3. Rezystor
- 1.4. Cewka
- 1.5. Kondensator
- 1.6. Niezależne źródło napięcia i prądu
- 1.7. Źródła sterowane
- 1.8. Prawa Kirchhoffa
- 1.9. Suma prądów w każdym węźle obwodu elektrycznego jest równa zeru
- 1.10. Prawo napięciowe
- 1.11. Przekształcenia obwodów
- 1.12. Połączenie szeregowe elementów
- 1.13. Połączenie równoległe elementów
- 1.14. Transfiguracja gwiazda-trójkąt i trójkąt-gwiazda
- 2. Analiza obwodów w stanie ustalonym przy wymuszeniu sinusoidalnym
- 3. Moce w obwodach RLC przy wymuszeniu sinusoidalnym
- 4. Metody analizy złożonych obwodów RLC w stanie ustalonym przy wymuszeniu sinusoidalnym
1. Podstawowe pojęcia i prawa obwodów elektrycznych
Teoria obwodów jest jedną z podstawowych dziedzin elektrotechniki obejmującą teoretyczną stronę zjawisk występujących w obwodach elektrycznych, w szczególności metody obliczeń rozpływu prądów i rozkładu napięć obwodu w stanie ustalonym i nieustalonym.
Wykład pierwszy wprowadza podstawowe pojęcia i prawa obwodów elektrycznych, w tym prąd i napięcie, elementy liniowe obwodu w postaci rezystora, cewki i kondensatora oraz źródła sterowane i niezależne. Najważniejszym prawem teorii obwodów jest prawo prądowe i napięciowe Kirchhoffa, podane tutaj w postaci ogólnej. Z prawa Kirchhoffa wynikają reguły upraszczania obwodów, zdefiniowane dla połączenia szeregowego, równoległego oraz transfiguracji gwiazda-trójkąt i trójkąt-gwiazda.
1.1. Podstawowe pojęcia obwodów
W elektrotechnice przyjmuje się, że nośnikami elektryczności są cząstki elementarne: elektrony i protony występujące w atomie. W przypadku przewodników elektrycznych najważniejszą rolę odgrywają elektrony swobodne, stanowiące trwałe nośniki ujemnego ładunku q, wyzwolone z przyciągania jądra atomu oraz jony, stanowiące cząsteczki naładowane dodatnio lub ujemnie. Ładunek elektryczny elektronu, oznaczany jest literą e a jego wartość e=1,602×10-19C.
Prąd elektryczny jest uporządkowanym ruchem ładunków elektrycznych i jest utożsamiany w teorii obwodów z natężeniem prądu elektrycznego. W ogólności definiowany jest jako granica stosunku ładunku elektrycznego przepływającego przez przekrój poprzeczny elementu do rozpatrywanego czasu, gdy czas ten dąży do zera. Prąd elektryczny oznaczany będzie literą i (dużą lub małą). Jest wielkością skalarną a jej jednostką w układzie SI jest amper (A). Prąd mierzymy przyrządem zwanym amperomierzem, włączanym szeregowo do gałęzi, której prąd chcemy zmierzyć. Przyjmuje się, że amperomierz ma impedancję wewnętrzną równą zeru, a więc nie wpływa na rozpływy prądów w obwodzie.
Każdemu punktowi w środowisku przewodzącym prąd elektryczny można przyporządkować pewien potencjał mierzony względem określonego punktu odniesienia. Różnica potencjałów między dwoma punktami tego środowiska nazywana jest napięciem elektrycznym. Jednostką napięcia elektrycznego jest volt (V). Napięcie pomiędzy dwoma punktami obwodu elektrycznego mierzy się przyrządem zwanym woltomierzem, włączanym równolegle między punkty, których różnicę potencjałów chcemy mierzyć. Przyjmuje się przy tym, że impedancja wewnętrzna woltomierza jest bliska nieskończoności, a więc woltomierz pomiarowy nie wpływa na rozkład napięć i rozpływ prądów w obwodzie.
1.2. Podstawowe elementy obwodu elektrycznego
Za obwód elektryczny uważać będziemy takie połączenie elementów ze sobą, że istnieje możliwość przepływu prądu w tym połączeniu. Obwód jest odwzorowywany poprzez schemat połączeń elementów, na którym zaznaczone są symbole graficzne elementów oraz sposób ich połączenia ze sobą, tworzący określoną strukturę.
W strukturze obwodu elektrycznego poza elementami wyróżnić można gałęzie, węzły i oczka. Gałąź obwodu jest tworzona przez jeden lub kilka elementów połączonych ze sobą w określony sposób. Węzłem obwodu jest zacisk będący końcówką gałęzi, do którego można dołączyć następną gałąź lub kilka gałęzi. Gałąź obwodu tworzą elementy ograniczone dwoma węzłami. Oczko obwodu to zbiór gałęzi połączonych ze sobą, tworzących drogę zamkniętą dla prądu elektrycznego. Oczko ma tę właściwość, że po usunięciu dowolnej gałęzi ze zbioru pozostałe gałęzie nie tworzą drogi zamkniętej. W obwodzie o zadanej strukturze istnieje ściśle określona liczba węzłów, natomiast liczba oczek jest wprawdzie skończona ale bliżej nieokreślona.
Element jest częścią składową obwodu niepodzielną pod względem funkcjonalnym bez utraty swych cech charakterystycznych. Na elementy obwodu składają się źródła energii elektrycznej oraz elementy akumulujące energię lub rozpraszające ją. W każdym elemencie mogą zachodzić dwa lub nawet wszystkie trzy wymienione tu procesy, choć jeden z nich jest zwykle dominujący. Element jest idealny jeśli charakteryzuje go tylko jeden rodzaj procesu energetycznego.
Elementy posiadające zdolność akumulacji oraz rozpraszania energii tworzą klasę elementów pasywnych. Nie wytwarzają one energii a jedynie ją przetwarzają. Najważniejsze z nich to rezystor, kondensator oraz cewka. Elementy mające zdolność generacji energii nazywane są źródłami. Zaliczamy do nich niezależne źródło napięcia i prądu oraz źródła sterowane.
Każdy element obwodu może być opisany równaniami algebraicznymi lub różniczkowymi, wiążącymi prąd i napięcie na jego zaciskach. Element jest liniowy, jeśli równanie opisujące go jest liniowe. W przeciwnym wypadku element jest nieliniowy.
1.3. Rezystor
Rezystor, zwany również opornikiem należy do klasy elementów pasywnych rozpraszających energię. W teorii obwodów rezystor uważa się za element idealny i przypisuje mu tylko jedną cechę (parametr), zwaną rezystancją lub oporem. W dalszej części rozważać będziemy wyłącznie rezystor liniowy. Rezystancję (oporność) oznaczać będziemy literą R a jej odwrotność jest nazywana konduktancją i oznaczana literą G, przy czym R = 1/G. Symbol graficzny rezystora liniowego przedstawiony jest na rys. 1.1.
Rys. 1.1. Symbol graficzny rezystora liniowego
Opis matematyczny rezystora wynika z prawa Ohma, zgodnie z którym
| \(u_R=Ri_R\) | (1.1) |
Rezystancja rezystora liniowego przyjmuje określoną wartość (najczęściej stałą). Jednostką rezystancji jest om (W) a konduktancji siemens (S).
W realizacji praktycznej opornik jest wykonywany często z drutu metalowego o długości l, polu przekroju poprzecznego S i rezystancji właściwej r. Rezystancja takiego opornika jest wprost proporcjonalna do l i r a odwrotnie proporcjonalna do S, stąd R = r l/S.
1.4. Cewka
Cewka zwana również induktorem należy również do klasy elementów pasywnych. Ma zdolność gromadzenia energii w polu magnetycznym. Cewce idealnej przypisuje się tylko jedną właściwość, zwaną indukcyjnością własną (w skrócie indukcyjnością) L. W przypadku cewki liniowej indukcyjność definiuje się w postaci stosunku strumienia Y skojarzonego z cewką do prądu płynącego przez nią, to znaczy
| \(L=\frac{\Psi}{i_L}\) | (1.2) |
Strumień skojarzony Y cewki o z zwojach jest równy sumie strumieni wszystkich zwojów cewki, to jest \(\Psi=z\varphi\) (φ - strumień skojarzony z jednym zwojem cewki, z – liczba zwojów). Jednostką strumienia jest weber (Wb), przy czym Wb=Vs, a indukcyjności henr (H), przy czym 1H = 1Ws. Napięcie cewki wyrażone jest jako pochodna strumienia względem czasu
| \(u_L=\frac{d\Psi}{dt}\) | (1.3) |
W przypadku cewki liniowej o indukcyjności L niezależnej od czasu, dla której strumień jest iloczynem prądu i indukcyjności L, \(\Psi=Li_L\) , relacja napięciowo-prądowa upraszcza się do postaci
| \(u_L=L\frac{di_L}{dt}\) | (1.4) |
Na rys. 1.2 przedstawiono symbol graficzny cewki liniowej o indukcyjności L.
Rys. 1.2. Symbol graficzny cewki liniowej
Zauważmy, że przy stałej wartości prądu cewki i stałej wartości indukcyjności L napięcie na niej jest równe zeru, gdyż pochodna wartości stałej względem czasu jest równa zeru. Stąd cewka w stanie ustalonym obwodu przy prądzie stałym zachowuje się jak zwarcie (napięcie między końcówkami elementu równe zeru).
1.5. Kondensator
Kondensator jest elementem pasywnym, w którym istnieje możliwość gromadzenia energii w polu elektrycznym. Kondensatorowi idealnemu przypisuje się tylko jedną właściwość zwaną pojemnością C. W przypadku kondensatora liniowego pojemność C jest definiowana jako stosunek ładunku q zgromadzonego w kondensatorze do napięcia między okładzinami tego kondensatora
| \(C=\frac{q}{u_C}\) | (1.5) |
W układzie SI jednostką ładunku jest kulomb (C), przy czym kulomb = As, a pojemności farad (F), przy czym 1 F = 1 C/V. Zależność wiążąca napięcie i prąd kondensatora dana jest w postaci równania różniczkowego
| \(i_C=C\frac{du_C}{dt}\) | (1.6) |
Symbol graficzny kondensatora przedstawiony jest na rys. 1.3.
Rys. 1.3. Symbol graficzny kondensatora
Podobnie jak w przypadku cewki, jeśli napięcie na zaciskach kondensatora jest stałe, jego prąd jest równy zeru (pochodna wartości stałej względem czasu jest zerem). Kondensator zachowuje się wtedy jak przerwa (pomimo istnienia napięcia prąd nie płynie).
1.6. Niezależne źródło napięcia i prądu
Źródło niezależne prądu bądź napięcia, zwane w skrócie źródłem prądu i źródłem napięcia, jest elementem aktywnym, generującym energię elektryczną, powstającą zwykle z zamiany innego rodzaju energii, na przykład z energii mechanicznej, słonecznej, jądrowej itp. W teorii obwodów rozważać będziemy źródła idealne należące do klasy źródeł napięciowych bądź prądowych. Symbol idealnego niezależnego źródła napięcia przedstawiony jest na rys. 1.4a, natomiast źródła prądu na rys. 1.4.b.
Rys. 1.4. Symbole graficzne niezależnego źródła a) napięcia, b) prądu
Niezależne źródła prądu i napięcia mają następujące właściwości.
- Napięcie na zaciskach idealnego źródła napięcia nie zależy od prądu przepływającego przez to źródło, a zatem nie zależy od jego obciążenia.
- Przy stałym napięciu u panującym na zaciskach oraz prądzie i wynikającym z obciążenia, rezystancja wewnętrzna idealnego źródła napięciowego, definiowana jest w postaci zależności różniczkowej \(R_w=\frac{du}{di}=0\) . Stąd idealne źródło napięcia charakteryzuje się rezystancją wewnętrzna równą zeru (zwarcie z punktu widzenia rezystancyjnego).
- Prąd idealnego źródła prądu nie zależy od obciążenia tego źródła, a więc od napięcia panującego na jego zaciskach.
- Przy stałym prądzie płynącym przez idealne źródło prądowe i dowolnym (bliżej nieokreślonym) napięciu panującym na jego zaciskach rezystancja wewnętrzna idealnego źródła prądowego jest równa nieskończoności. Stąd idealne źródło prądowe z punktu widzenia rezystancyjnego reprezentuje sobą przerwę.
Rys. 1.5 przedstawia charakterystyki prądowo-napięciowe obu rodzajów idealnych źródeł niezależnych: napięcia (rys. 1.5a) i prądu (rys. 1.5b).
Rys. 1.5. Charakterystyki prądowo-napięciowe idealnych źródeł niesterowanych:
a) źródło napięcia, b) źródło prądu
Dla źródła napięciowego charakterystyka jest równoległa do osi prądowej (wartość napięcia u stała), a dla źródła prądowego równoległa do osi napięciowej (wartość prądu i stała). Tak podane charakterystyki odnoszą się do źródeł stałych. W przypadku źródeł sinusoidalnych idealność jest rozumiana jako stałość parametrów źródła (amplituda, faza początkowa oraz częstotliwość niezależne od obciążenia).
Przykładami źródła napięcia stałego jest akumulator, źródła napięcia zmiennego - generator synchroniczny, źródła prądowego - elektroniczny zasilacz prądowy o stabilizowanym, niezależnym od obciążenia prądzie.
1.7. Źródła sterowane
W odróżnieniu od źródeł niezależnych, których prąd lub napięcie (bądź parametry charakteryzujące je, np. amplituda i częstotliwość) były stałe, ustalone na etapie wytworzenia, wielkości te dla źródeł sterowanych z definicji zależą od wielkości sterujących, którymi mogą być prąd lub napięcie dowolnego innego elementu w obwodzie.
- Źródło sterowane jest więc elementem czterozaciskowym i charakteryzuje się tym, że napięcie lub prąd na jego zaciskach wyjściowych są proporcjonalne do napięcia lub prądu związanego z drugą parą zacisków sterujących. Wyróżnić można cztery rodzaje źródeł sterowanych: źródło napięcia sterowane napięciem, źródło napięcia sterowane prądem, źródło prądu sterowane napięciem i źródło prądu sterowane prądem.
Równania źródeł sterowanych
- źródło napięcia sterowane napięciem
\(u_2=au_1\)
- źródło napięcia sterowane prądem
\(u_2=ri_1\)
- źródło prądu sterowane napięciem
\(i_2=gu_1\)
- źródło prądu sterowane prądem
\(i_2=bi_1\)
W równaniach tych wielkości oznaczone wskaźnikiem 2 oznaczają wielkości wyjściowe, a wskaźnikiem 1 – wielkości sterujące.
Schematy graficzne wszystkich wymienionych tu rodzajów źródeł sterowanych prądu i napięcia przedstawione są na rys. 1.6.
Rys. 1.6. Schematy graficzne źródeł sterowanych
Wielkości r, g oraz a i
1.8. Prawa Kirchhoffa
Pod pojęciem analizy obwodu elektrycznego rozumie się proces określania rozpływu prądów i rozkładu napięć w obwodzie przy założeniu, że znana jest struktura obwodu oraz wartości wszystkich jego elementów. Podstawę analizy obwodów elektrycznych stanowią prawa Kirchhoffa, podane przez niemieckiego fizyka Gustawa Kirchhoffa w dziewiętnastym wieku. Wyróżnia się dwa prawa określające rozpływ prądów i rozkład napięć w obwodzie. Pierwsze prawo Kirchhoffa kojarzy się zwykle z bilansem prądów w węźle obwodu elektrycznego a drugie z bilansem napięć w oczku.
1.9. Suma prądów w każdym węźle obwodu elektrycznego jest równa zeru
Suma prądów w każdym węźle obwodu elektrycznego jest równa zeru
| \(\sum_{k} i_k=0\) | (1.7) |
Sumowanie dotyczy wszystkich prądów, które dopływają lub odpływają z danego oczka, przy czym wszystkie prądy wpływające do węzła brane są z jednakowym znakiem a wszystkie prądy wypływające z węzła ze znakiem przeciwnym (nie jest istotne czy znak plus dotyczy prądów wpływających czy wypływających). Sposób tworzenia równania prądowego Kirchhoffa zilustrujemy dla jednego węzła obwodu przedstawionego na rys. 1.7.
Rys. 1.7. Przykład węzła obwodu elektrycznego
Prawo Kirchhoffa dla tego węzła z uwzględnieniem kierunków prądów w węźle zapiszemy w postaci
\(i_1+i_2+i_3-i_4-i_5=0\)
Można je również zapisać jako bilans prądów dopływających i odpływających od węzła w postaci
\(i_1+i_2+i_3=i_4+i_5\)
Dla każdego obwodu można napisać dokładnie n-1 niezależnych równań prądowych, gdzie n oznacza całkowitą liczbę węzłów a (n-1) liczbę węzłów niezależnych. Bilans prądów w pozostałym n-tym węźle obwodu wynika z równań prądowych napisanych dla n-1 węzłów (jest to węzeł zależny zwany węzłem odniesienia). Wybór węzła odniesienia jest całkowicie dowolny.
1.10. Prawo napięciowe
Suma napięć w każdym oczku obwodu elektrycznego jest równa zeru
| \(\sum_{k} u_k=0\) | (1.8) |
Sumowanie dotyczy napięć gałęziowych występujących w danym oczku zorientowanych względem dowolnie przyjętego kierunku odniesienia. Napięcie gałęziowe zgodne z tym kierunkiem jest brane z plusem a przeciwne z minusem. Sposób pisania równań wynikających z prawa napięciowego Kirchhoffa pokażemy na przykładzie oczka obwodu przedstawionego na rys. 1.8.
Rys. 1.8. Przykład oczka obwodu z oznaczeniami napięć gałęziowych
Uwzględniając kierunki napięć gałęziowych równanie napięciowe Kirchhoffa dla tego oczka przyjmie postać
\(u_1+u_2+u_3-u_4-e=0\)
Można je również zapisać jako bilans napięć źródłowych i odbiornikowych w postaci
\(e=u_1+u_2+u_3-u_4\)
Dla każdego obwodu można napisać tyle równań oczkowych ile oczek wyodrębnimy w tym obwodzie, przy czym część równań oczkowych będzie równaniami zależnymi (wynikającymi z liniowej kombinacji innych równań). Minimalna liczba równań oczkowych branych pod uwagę w analizie jest więc równa liczbie oczek niezależnych.
Napiszemy równania Kirchhoffa dla obwodu z rys. 1.9.
Rys. 1.9. Schemat obwodu poddanego analizie w przykładzie 1.1
Rozwiązanie
Zgodnie z prawami Kirchhoffa równania obwodu przyjmą następującą postać.
- Równania prądowe:
\(i_{L1}-i_{L2}-i_C=0\)
\(i_{L2}-i_{R1}-i_{R2}=0\)
\(i_{L1}=i\)
- Równania napięciowe:
\(u_C-u_{L2}-u_{R1}=0\)
\(u_{R1}-u_{R2}-e=0\)
Przedstawiony tu układ równań uzupełniony o równania elementów jest wystarczający do uzyskania wszystkich wielkości prądowych bądź napięciowych w obwodzie. Po takim uzupełnieniu uzyskuje się pełny opis obwodu a jego rozwiązanie pozwala wyznaczyć pełny rozpływ prądów i rozkład napięć w obwodzie.
Szczególnie proste zależności otrzymuje się dla obwodu rezystancyjnego, zawierającego oprócz źródeł wymuszających jedynie rezystory oraz (ewentualnie) źródła sterowane o rzeczywistych współczynnikach sterowania. Dla takich obwodów równania elementów rezystancyjnych są dane w postaci zależności algebraicznych, które wstawione do równań Kirchhoffa pozwalają utworzyć układ równań algebraicznych o liczbie zmiennych równych liczbie równań. Sposób tworzenia takiego układu równań pokażemy na przykładzie obwodu z rys. 1.10.
Należy określić rozpływ prądów i rozkład napięć w obwodzie rezystancyjnym o strukturze przedstawionej na rys. 1.10. Wartości elementów są następujące: R1 = 1W, R2 = 2W, R3 = 3W, R4 = 4W, e = 10V, iz1 = 2A, iz2 = 5A.
Rys. 1.10. Struktura obwodu poddanego analizie w przykładzie 1.2
Rozwiązanie
Z równań Kirchhoffa otrzymuje się
\(i_{z1}-i_1-i_2-i_4=0\)
\(i_2+i_4+i_{z2}-i_3=0\)
\(u_{R1}-u_{R2}+e-u_{R3}=0\)
\(u_{R2}-e-u_{R4}=0\)
Równania elementów rezystancyjnych: \( u_{R1}=R_1i_1,\) \(u_{R2}=R_2i_2,\) \(u_{R3}=R_3i_3, \) \(u_{R4}=R_4i_4\) tworzą wspólnie z równaniami Kirchhoffa następujący układ równań algebraicznych:
\(i_1+i_2+i_4=i_{z1}\)
\(i_2-i_3+i_4=-i_{z2}\)
\(R_1i_1-R_2i_2-R_3i_3=-e\)
\(R_2i_2-R_4i_4=e\)
Po wstawieniu danych liczbowych do powyższych równań otrzymuje się:
\(i_1+i_2+i_4=2\)
\(i_2-i_3+i_4=-5\)
\(i_1-2i_2-3i_3=-10\)
\(2i_2-4i_4=10\)
W wyniku rozwiązania tego układu równań otrzymuje się: i1 = 3,187A, i2 = 0,875A, i3 = 3,812A oraz i4 = -2,062A. Łatwo sprawdzić przez podstawienie obliczonych wartości do układu równań, że bilans prądów w każdym węźle oraz bilans napięć w każdym oczku obwodu jest zerowy.
1.11. Przekształcenia obwodów
W analizie obwodów elektrycznych ważną rolę odgrywa upraszczanie struktury obwodu, polegające na zastępowaniu wielu elementów połączonych szeregowo lub równolegle poprzez jeden element zastępczy. Umożliwia to zmniejszenie liczby równań w opisie obwodu i uproszczenie etapu rozwiązania tych równań. Wyróżnić można cztery podstawowe rodzaje połączeń elementów, do których stosuje się przekształcenie. Są to:
- połączenie szeregowe
- połączenie równoległe
- połączenie gwiazdowe
- połączenie trójkątne.
1.12. Połączenie szeregowe elementów
W połączeniu szeregowym elementów koniec jednego elementu jest bezpośrednio połączony z początkiem następnego. Rys. 1.11 przedstawia schemat ogólny połączenia szeregowego rezystorów.
Rys. 1.11. Połączenie szeregowe elementów
Prąd każdego elementu obwodu jest jednakowy i równy i, natomiast napięcie na zaciskach zewnętrznych obwodu jest równe sumie napięć poszczególnych elementów tworzących połączenie. Napięciowe równanie Kirchhoffa dla obwodu z rys. 1.11 przyjmuje więc postać
| \(u=(R_1+R_2+...+R_N)i\) | (1.9) |
Przy oznaczeniu sumy rezystancji przez R
| \(R=R_1+R_2+...+R_N\) | (1.10) |
otrzymuje się uproszczenie N rezystorów połączonych szeregowo do jednego rezystora zastępczego o rezystancji R opisanej wzorem (1.10). Rezystancja zastępcza (wypadkowa) połączenia szeregowego rezystorów jest równa sumie rezystancji poszczególnych elementów tworzących to połączenie.
1.13. Połączenie równoległe elementów
W połączeniu równoległym początki wszystkich elementów, podobnie jak również ich końce są ze sobą bezpośrednio połączone, jak to pokazano dla elementów rezystancyjnych na rys. 1.12.
Rys. 1.12. Połączenie równoległe elementów
Z połączenia tego wynika, że napięcie na wszystkich elementach jest jednakowe a prąd wypadkowy i jest równy sumie prądów wszystkich elementów obwodu. Prądowe prawo Kirchhoffa dla obwodu z rys. 1.12 można więc zapisać w postaci
| \(i=(G_1+G_2+...+G_N)u\) | (1.11) |
przy czym Gi (i = 1, 2, ..., N) stanowią konduktancje rezystorów, Gi=1/Ri. Przy oznaczeniu sumy konduktancji przez G, gdzie
| \(G=G_1+G_2+...+G_N\) | (1.12) |
otrzymuje się uproszczenie N rezystorów połączonych równolegle do jednego rezystora zastępczego o konduktancji G opisanej wzorem (1.12). W połączeniu równoległym rezystorów konduktancja zastępcza (wypadkowa) jest równa sumie konduktancji poszczególnych rezystorów tworzących to połączenie. Rezystancję zastępczą dla N równolegle połączonych rezystorów obliczyć można jako odwrotność konduktancji zastępczej G, R=1/G.
Szczególnie prosty jest wzór na rezystancję zastępczą dla 2 rezystorów połączonych równolegle. W tym przypadku \(G=G_1+G_2\). Uwzględniając, że \(G=1/R\) po prostych przekształceniach otrzymuje się
\(R=\frac{R_1R_2}{R_1+R_2}\)
Należy jednak podkreślić, że przy trzech (i więcej) elementach połączonych równoległe wygodniejsze jest operowanie na konduktancjach a przejście na rezystancję zastępczą wykonuje się w ostatnim kroku po ustaleniu wartości sumy konduktancji.
1.14. Transfiguracja gwiazda-trójkąt i trójkąt-gwiazda
Operowanie uproszczonym schematem wynikającym z połączenia szeregowego i równoległego elementów jest najwygodniejszym sposobem redukcji obwodu. W przypadku gdy nie ma elementów połączonych szeregowo lub równolegle możliwe jest dalsze uproszczenie obwodu przez zastosowanie przekształcenia gwiazda-trójką lub trójkąt-gwiazda. Przyjęte oznaczenia elementów rezystancyjnych trójkąta i gwiazdy są przedstawione na rys. 1.13.
Rys. 1.13. Połączenie a) trójkątne i b) gwiazdowe elementów
Transfiguracja trójkąta na gwiazdę lub gwiazdy na trójkąt polega na przyporządkowaniu danej konfiguracji elementów konfiguracji zastępczej, równoważnej jej z punktu widzenia zacisków zewnętrznych (te same prądy przy tych samych napięciach międzyzaciskowych). Dla uzyskania niezmienionych prądów zewnętrznych obwodu gwiazdy i trójkąta rezystancje między parami tych samych zacisków gwiazdy i trójkąta powinny być takie same. Zostało udowodnione, że warunki powyższe są automatycznie spełnione, jeśli przy zamianie gwiazdy na trójkąt spełnione są następujące warunki na rezystancje
| \(R_{12}=R_1+R_2+\frac{R_1R_2}{R_3}\) | (1.13) |
| \(R_{23}=R_2+R_3+\frac{R_2R_3}{R_1}\) | (1.14) |
| \(R_{31}=R_3+R_1+\frac{R_3R_1}{R_2}\) | (1.15) |
Podobnie przy zamianie trójkąta na gwiazdę rezystancje gwiazdy muszą spełniać warunki
| \(R_1=\frac{R_{12}R_{31}}{R_{12}+R_{23}+R_{31}}\) | (1.16) |
| \(R_2=\frac{R_{23}R_{12}}{R_{12}+R_{23}+R_{31}}\) | (1.17) |
| \(R_3=\frac{R_{31}R_{23}}{R_{12}+R_{23}+R_{31}}\) | (1.18) |
Przekształcenia równoważne obwodu wykorzystujące reguły połączenia szeregowego, równoległego oraz przekształcenia gwiazda-trójkąt i trójkąt-gwiazda umożliwiają dalszą redukcję tego obwodu i po wykonaniu odpowiedniej liczby przekształceń pozwalają zawsze na sprowadzenie go do pojedynczego elementu zastępczego.
Określić rezystancję zastępczą obwodu przedstawionego na rys. 1.14, widzianą z zacisków 1-2. Wartości rezystancji są następujące: \(R_1=2\Omega,\) \(R_2=4\Omega,\)\(R_3=3\Omega,\)\(R_4=2\Omega,\)\(R_5=4\Omega,\)\(R_6=5\Omega,\)\(R_7=5\Omega\) oraz \(R_8=10\Omega\).
Rys. 1.14. Struktura obwodu do przykładu 1.3
Rozwiązanie
Z punktu widzenia zacisków wejściowych 1-2 w obwodzie nie można wyróżnić żadnego połączenia szeregowego czy równoległego elementów upraszczających obwód. Dla uproszczenia struktury tego obwodu konieczne jest więc zastosowanie przekształcenia gwiazda-trójkąt lub trójkąt-gwiazda w stosunku do rezystorów położonych najdalej od węzłów wejściowych (w wyniku przekształcenia nie mogą ulec likwidacji węzły wejściowe obwodu). Zamieniając gwiazdę złożoną z rezystorów R2, R3, i R5 na równoważny jej trójkąt otrzymuje się
\(R_{23}=3+4+\frac{3\cdot4}{4}=10\)
\(R_{35}=3+4+\frac{3\cdot4}{4}=10\)
\(R_{25}=4+4+\frac{4\cdot4}{3}=13,33\)
Schemat obwodu po tym przekształceniu przedstawiony jest na rys. 1.15a.
Rys. 1.15. Schemat obwodu z rys. 1.14 po przekształceniu gwiazda-trójkąt
W obwodzie tym można już wyróżnić połączenia równoległe elementów R1 i R23 oraz R4 i R35. Wykorzystując regułę upraszczania elementów połączonych równolegle otrzymuje się (rys. 1.15b)
\(R_{z1}=\frac{R_1\cdot R_{23}}{R_1+R_{23}}=1,667\)
\(R_{z2}=\frac{R_4\cdot R_{35}}{R_4+R_{35}}=1,667 \)
Rezystory Rz1 i Rz2 są połączone szeregowo. Ich rezystancja zastępcza jest równa
Rz3 = Rz1 + Rz2 = 3,333
Jest ona połączona równolegle z rezystorem R25. Stąd rezystancja zastępcza tego połączenia wynosi (rys. 1.15c)
\(R_{z4}=\frac{3,333\cdot13,33}{3,333+13,33}=2,667\)
Rezystory R6, Rz4 i R7 są połączone szeregowo. Ich rezystancja zastępcza wynosi więc
Rz5 = R6 + Rz4 + R7 = 12,667
Rezystancja ta jest z kolei połączona równolegle z rezystancją R8 tworząc wypadkową rezystancję obwodu widzianą z zacisków zewnętrznych. Stąd całkowita rezystancja zastępcza obwodu wyraża się wzorem
\(R_{we}=\frac{R_{z5}R_8}{R_{z5}+R_8}=\frac{12,667\cdot10}{12,667+10}=5,588\Omega\)
Należy zaznaczyć, że przekształcenia gwiazda-trójkąt i trójkąt-gwiazda są bardziej złożone obliczeniowo w stosunku do reguły upraszczania połączenia szeregowego i równoległego. Stosuje się je tylko wtedy, gdy w obwodzie nie da się wyróżnić żadnych połączeń szeregowych i równoległych.
2. Analiza obwodów w stanie ustalonym przy wymuszeniu sinusoidalnym
Spośród wielu różnych rodzajów wymuszeń stosowanych w obwodach elektrycznych, do najważniejszych należy wymuszenie sinusoidalne, ze względu na to, że w praktyce codziennej mamy do czynienia z napięciem i prądem sinusoidalnym generowanym w elektrowniach. Analiza obwodów RLC przy wymuszeniu sinusoidalnym nastręcza pewne problemy związane z koniecznością rozwiązania układu równań różniczkowych, wynikających z opisu ogólnego kondensatorów i cewek. Szczególnie ważny w praktyce inżynierskiej jest stan ustalony obwodu. W stanie ustalonym odpowiedzi obwodu liniowego przyjmują taką samą formę jak wymuszenia. Przy sinusoidalnym wymuszeniu odpowiedź jest również sinusoidalna o tej samej częstotliwości co wymuszenie choć o innej amplitudzie i fazie początkowej. Analiza obwodów przy wymuszeniu sinusoidalnym stanowi poważne wyzwanie obliczeniowe, które może być stosunkowo łatwo rozwiązane przy zastosowaniu rachunku symbolicznego liczb zespolonych.
W tym wykładzie poznamy metodę symboliczną analizy obwodów RLC w stanie ustalonym przy wymuszeniu sinusoidalnym. Dzięki tej metodzie układ równań różniczkowo-całkowych opisujących obwód RLC zostaje sprowadzony do układu równań algebraicznych typu zespolonego. Wprowadzone zostanie pojęcie wartości skutecznej zespolonej, impedancji i admitancji zespolonej oraz prawa Kirchhoffa dla wartości skutecznych zespolonych. Prawo prądowe i napięciowe Kirchhoffa dla obwodów RLC w metodzie symbolicznej stosuje się identycznie jak dla obwodów rezystancyjnych prądu stałego reprezentując elementy RLC poprzez impedancje zespolone. W rezultacie otrzymuje się wartości zespolone odpowiedzi, którym można przyporządkować wartości chwilowe zgodnie z metodą symboliczną. Ważnym elementem analizy są wykresy wektorowe przedstawiające na płaszczyźnie zespolonej relacje między wartościami skutecznymi zespolonymi prądów i napięć gałęziowych w obwodzie.
W końcowej części wykładu przedstawimy zjawiska w obwodzie RLC związane z rezonansem. Zjawiskiem rezonansu nazywamy taki stan obwodu RLC, w którym pomimo istnienia w obwodzie elementów reaktancyjnych prąd i napięcie są ze sobą w fazie. W stanie rezonansu przesunięcie fazowe prądu i napięcia jest więc zerowe, co oznacza, że kąt fazowy impedancji lub admitancji zespolonej obwodu jest także równy zeru. Obwód nie pobiera żadnej mocy biernej a ściśle mówiąc następuje zjawisko kompensacji tej mocy w obwodzie.
Rezonans wystąpić może w dowolnej konfiguracji elementów RLC, tym nie mniej bada się szczególne połączenia elementów prowadzące do tego zjawiska. Rezonans występujący w obwodzie, w którym elementy R, L, C są połączone szeregowo nazywamy rezonansem napięć lub rezonansem szeregowym. W przypadku, gdy rezonans dotyczy obwodu równoległego R, L, C taki rezonans nazywamy rezonansem prądów lub rezonansem równoległym.
2.1. Parametry sygnału sinusoidalnego
Sygnały sinusoidalne zwane również harmonicznymi są opisane w dziedzinie czasu następującym wzorem (w opisie przyjęto oznaczenie sygnału napięciowego)
| \(u(t)=U_msin{(}\omega t+\psi)\) | (2.1) |
Wielkości występujące w opisie mają następujące nazwy i oznaczenia:
- u(t) - wartość chwilowa napięcia
- Um - wartość maksymalna (szczytowa) napięcia zwana również amplitudą
- \(\psi\) - faza początkowa napięcia odpowiadająca chwili t=0
- \(\omega t+\psi\) - kąt fazowy napięcia w chwili t
- f=1/T - częstotliwość mierzona w hercach (Hz)
- T - okres przebiegu sinusoidalnego (mierzony w sekundach)
- \(\omega=2\pi f\) - pulsacja mierzona w radianach na sekundę.
W dalszych rozważaniach wartości chwilowe sygnałów oznaczać będziemy małą literą a wartości maksymalne, skuteczne i wielkości operatorowe dużą.
Rys. 2.1. Sygnał sinusoidalny
Rys. 2.1 przedstawia przebieg sygnału sinusoidalnego napięcia u(t) z oznaczeniami poszczególnych jego parametrów. Oś odciętych ma podwójne oznaczenie: czasu t oraz fazy (aktualny kąt fazowy (wt+ y)).
Przebiegi zmienne w czasie dobrze charakteryzuje wartość skuteczna. Dla przebiegu okresowego f(t) o okresie T jest ona definiowana w postaci
| \(F=\sqrt{\frac{1}{T}\int_{t_0}^{t_o+T}{f^2(t)dt}}\) | (2.2) |
Łatwo udowodnić, że wartość skuteczna przebiegu okresowego nie zależy od wybory fazy początkowej. W przypadku przebiegu sinusoidalnego napięcia u(t) =Um sin(wt+ y) jest równa
| \(U=\frac{U_m}{\sqrt2}\) | (2.3) |
a w przypadku prądu sinusoidalnego i(t) =Im sin(wt+ y)
| \(I=\frac{I_m}{\sqrt2}\) | (2.4) |
Dla sygnału sinusoidalnego wartość skuteczna jest więc \(\sqrt2\) razy mniejsza niż jego wartość maksymalna. Należy zauważyć, że napięcie stałe u(t)=U jest szczególnym przypadkiem sygnału sinusoidalnego, dla którego częstotliwość jest równa zeru (f=0) a wartość chwilowa jest stała i równa u(t)=Um sin(
Należy zauważyć, ze w elektrotechnice używa się również pojęcia wartości średniej sygnału, definiowanej jako uśredniona wartość sygnału za okres lub pół okresu funkcji okresowej, definiowana w postaci \(\frac{1}{T}\int_{t_0}^{t_0+T}{f(t)dt}\). Wartość średnia całookresowa dla sygnału sinusoidalnego jest równa zeru. Wartość średnia półokresowa jest różna od zera i równa 0,637Um.
2.2. Metoda symboliczna analizy obwodów RLC przy zastosowaniu liczb zespolonych
Analiza obwodów zawierających elementy RLC przy wymuszeniu sinusoidalnym napotyka na pewne trudności związane z wystąpieniem w opisie cewki i kondensatora równań różniczkowych. Trudności te łatwo jest pokonać w stanie ustalonym. Stanem ustalonym obwodu nazywać będziemy taki stan, w którym charakter odpowiedzi jest identyczny jak charakter wymuszenia, to znaczy odpowiedzią na wymuszenie sinusoidalne jest odpowiedź również sinusoidalna o tej samej częstotliwości choć o różnej amplitudzie i fazie początkowej. Dla stanu ustalonego obwodu wprowadzona zostanie metoda liczb zespolonych, zwana również metodą symboliczną, sprowadzająca wszystkie operacje różniczkowe i całkowe do działań algebraicznych na liczbach zespolonych.
Dla wprowadzenia tej metody przyjmijmy, że rozważany jest obwód szeregowy RLC (rys. 2.2) zasilany ze źródła napięcia sinusoidalnego \(u(t)=U_msin{(}\omega t+\psi)\).
Rys. 2.2. Połączenie szeregowe elementów RLC
Z prawa napięciowego Kirchhoffa wynika następujący związek między napięciami elementów tego obwodu
| \(u(t)=u_R+u_L+u_C\) | (2.5) |
Biorąc pod uwagę podstawowe zależności definicyjne dla rezystora, cewki i kondensatora
\(u_R=Ri\)
\( u_C=1/C\int i d t\)
\( u_L=L\frac{di}{dt} \)
otrzymuje się
| \(U_msin{(}\omega t+\psi)=Ri+\frac{1}{C}\int i d t+L\frac{di}{dt}\) | (2.6) |
Jest to równanie różniczkowo-całkowe opisujące zależności między wartościami chwilowymi prądu i napięcia wymuszającego w obwodzie. Pełne rozwiązanie tego równania sprowadza się do wyznaczenia dwu składowych prądu, stanowiących odpowiedź obwodu w stanie ustalonym i stanie przejściowym:
- składowej ustalonej, której charakter zmian w czasie jest taki sam jak sygnału wymuszającego (przy sinusoidalnym wymuszeniu odpowiedź również sinusoidalna o tej samej częstotliwości); jest to stan który zostanie osiągnięty przez obwód po czasie teoretycznie nieskończenie długim.
- składowej przejściowej odpowiadającej różnicy między rozwiązaniem rzeczywistym równania różniczkowego a składową ustaloną.
W praktyce składowa przejściowa zanika zwykle szybko w czasie i pozostaje jedynie składowa ustalona. Stan po zaniknięciu składowej przejściowej nazywamy stanem ustalonym obwodu.
Składową ustaloną odpowiedzi obwodu można otrzymać nie rozwiązując równania różniczkowego opisującego ten obwód a korzystając jedynie z metody liczb zespolonych (metody symbolicznej). Istotnym elementem tej metody jest zastąpienie przebiegów czasowych ich reprezentacją zespoloną. Przyjmijmy, że prąd \(i(t)=I_msin{(}\omega t+\Psi_i)\)i \(u(t)=U_msin{(}\omega t+\Psi_u)\)napięcie zastąpione zostały przez wektory wirujące w czasie, odpowiednio I(t) oraz U(t) określone w postaci
| \((t)=U_me^{j{\psi_u}}e^{j\omega t}\) | (2.7) |
| \(I(t)=I_me^{j\psi_i}e^{j\omega t}\) | (2.8) |
Po zastąpieniu wartości czasowych prądu i napięcia w równaniu (2.6) poprzez ich reprezentację w postaci wektorów wirujących otrzymuje się
| \(U(t)=RI(t)+L\frac{dI(t)}{dt}+\frac{1}{C}\int{I(t)dt}\) | (2.9) |
Po wykonaniu operacji różniczkowania i całkowania oraz pominięciu czynnika \(e^{j\omega t}\) występującego we wszystkich składnikach wzoru równanie powyższe przyjmuje postać
| \(\frac{U_m}{\sqrt2}e^{j\psi_u}=R\frac{I_m}{\sqrt2}e^{j\psi_i}+j\omega L\frac{I_m}{\sqrt2}e^{j\psi_i}+\frac{1}{j\omega C}\frac{I_m}{\sqrt2}e^{j\psi_i}\) | (2.10) |
Oznaczmy przez \(U=\frac{U_m}{\sqrt2}e^{j\psi_u}\)wartość skuteczną zespoloną napięcia, a przez \(I=\frac{I_m}{\sqrt2}e^{j\psi_i}\) wartość skuteczną zespoloną prądu. Wtedy równanie (2.10) można zapisać w postaci obowiązującej dla wartości skutecznych zespolonych
| \(U=RI+j\omega LI+\frac{1}{j\omega C}I\) | (2.11) |
Składnik
| \(U_R=RI\) | (2.12) |
odpowiada napięciu skutecznemu zespolonemu na rezystorze. Wielkość
| \(U_L=j\omega LI\) | (2.13) |
reprezentuje wartość skuteczną zespoloną napięcia na cewce, a składnik
| \(U_C=\frac{1}{j\omega C}I\) | (2.14) |
odpowiada wartości skutecznej zespolonej napięcia na kondensatorze. Wszystkie napięcia i prąd w obwodzie są wartościami zespolonymi.
Analizując postać równania (2.11) można zauważyć prostą analogię do równania opisującego obwód rezystancyjny. W tym celu wprowadzimy uogólnienie rezystancji w postaci pojęcia impedancji zespolonej wiążącej wartości skuteczne prądu i napięcia na elementach R, L, C w stanie ustalonym przy wymuszeniu sinusoidalnym. Z ostatnich równań na podstawie prawa Ohma można napisać następujące przyporządkowania:
- Dla rezystora
| \(Z_R=R\) | (2.15) |
impedancja ZR jest równa rezystancji tego rezystora.
- Dla cewki
| \(Z_L=j\omega L\) | (2.16) |
impedancja ZL jest liczbą zespoloną (urojoną) zależną liniowo od częstotliwości.
- Dla kondensatora
| \(Z_C=\frac{1}{j\omega C}=-j\frac{1}{\omega C}\) | (2.17) |
impedancja ZC jest także zespolona i odwrotnie proporcjonalna do częstotliwości.
Wartość \(X_L=\omega L\) nosi nazwę reaktancji indukcyjnej a wartość \(X_C=\frac{1}{\omega C}\) reaktancji pojemnościowej. W związku z powyższym można napisać \(Z_L=jX_L\), \(Z_C=-jX_C\) .
Wprowadzając oznaczenie wypadkowej impedancji obwodu przez Z, gdzie \(Z=Z_R+Z_L+Z_C\) zależność prądowo-napięciową w obwodzie szeregowym RLC można zapisać w postaci, znanej jako prawo Ohma dla wartości symbolicznych
| \(U=ZI\) | (2.18) |
lub
| \(I=\frac{U}{Z}=\left|I\right|e^{j\psi_i}\) | (2.19) |
gdzie moduł prądu
| \(\left|I\right|=\frac{\left|U\right|}{\left|Z\right|}=\frac{\left|U\right|}{\sqrt{R^2+(\omega L-1/(\omega C))^2}}\) | (2.20) |
natomiast kąt fazowy prądu
| \(\psi_i=\psi_u-\mathrm{arctg}\frac{\omega L-1/(\omega C)}{R}\) | (2.21a) |
Faza początkowa wektora napięcia wymuszającego jest tu oznaczona przez \(\psi_u\) , a faza początkowa wektora prądu – przez \(\psi_i\) . Różnica faz nazywana jest przesunięciem fazowym prądu względem napięcia i oznaczana literą \(\phi\) , przy czym
| \(\phi=\psi_u-\psi_i=arctg{\frac{\omega L-1/(\omega C)}{R}}\) | (2.21b) |
Kąt przesunięcia fazowego \(\phi\) odgrywa ogromną rolę w elektrotechnice, zwłaszcza w zagadnieniach mocy. Kąt przesunięcia fazowego jest uważany za dodatni dla obwodów o charakterze indukcyjnym a za ujemny dla obwodów o charakterze pojemnościowym.
Zauważmy, że wartościom skutecznym zespolonym prądu oraz napięcia można przyporządkować funkcję czasu. Biorąc pod uwagę, że przejście z przebiegu czasowego na opis zespolony (symboliczny) odbywa się według schematu
| \(u(t)=U_msin{(}\omega t+\psi_u)\rightarrow\frac{U_m}{\sqrt2}e^{j\psi_u}\) | (2.22) |
powrót z wartości zespolonej do postaci czasowej polega na pomnożeniu modułu wartości skutecznej przez \(\sqrt2\) i uzupełnieniu wyniku przez dopisanie funkcji \(sin{(}\omega t+\psi_u)\). Stąd przykładowo, jeśli wynik zespolony prądu dany jest w postaci \(=10e^{j5{0^\circ}}\) , to odpowiadający mu przebieg czasowy ma postać \(i(t)=10\sqrt2sin{(}\omega t+50^\circ)\). Istnieje również ścisła analogia między konduktancją (odwrotność rezystancji) a odwrotnością impedancji.
Analogicznie do pojęcia konduktancji w obwodzie rezystancyjnym wprowadza się pojęcie admitancji zespolonej dla obwodu RLC. Admitancja jest definiowana jako odwrotność impedancji. Oznaczana jest najczęściej literą Y, przy czym
| Y = 1/Z | (2.23) |
Admitancja kondensatora jest równa \(Y_C=j\omega C\) , cewki \(Y_L=\frac{1}{j\omega L}=-j\frac{1}{\omega L}\) , natomiast admitancja rezystora jest równa jego konduktancji YR=G=1/R. Podobnie odwrotność reaktancji X nosi specjalną nazwę susceptancji. Wartość susceptancji dla kondensatora jest równa \(B_C=\omega C\), natomiast dla cewki \(B_L=1/\omega L\) .
2.3. Prawa Kirchhoffa dla wartości symbolicznych
Po zastąpieniu wartości rzeczywistych w metodzie symbolicznej przez wartości zespolone równania różniczkowe zostały zastąpione przez równania algebraiczne typu zespolonego. Nastąpiła zatem algebraizacja równań opisujących obwód. Wszystkie elementy RLC traktowane są w podobny sposób i reprezentowane przez swoje impedancje zespolone, interpretowane jako uogólnienie rezystancji. Dla obwodu reprezentowanego w postaci symbolicznej zespolonej obowiązują prawa Kirchhoffa, które mają identyczną postać jak dla obwodu rzeczywistego, z tą różnicą, że zamiast wielkości chwilowych używa się wielkości zespolonych.
Prawo prądowe Kirchhoffa
Suma algebraiczna prądów zespolonych w dowolnym węźle obwodu elektrycznego jest równa zeru, co zapiszemy w postaci
| \(\sum_{k}{I_k=0}\) | (2.24) |
W równaniu tym wszystkie prądy dane są w postaci zespolonej.
Prawo napięciowe Kirchhoffa
Suma algebraiczna napięć zespolonych w każdym oczku obwodu elektrycznego jest równa zeru, co zapiszemy w postaci
| \(\sum_{k}{U_k=0}\) | (2.25) |
W równaniu tym symbolem U oznaczono wszystkie napięcia w postaci zespolonej, zarówno na gałęziach pasywnych jak i źródłowych obwodu. Sposób sumowania (znak plus lub minus) zarówno prądów jak i napięć jest taki sam jak w przypadku operowania wartościami rzeczywistymi.
Podsumowując, metoda symboliczna analizy obwodu w stanie ustalonym składa się z następujących etapów.
- Przejście z przebiegu czasowego na opis zespolony (symboliczny) dla źródeł prądu i napięcia
\(u(t)=U_msin{(}\omega t+\psi_u)\rightarrow\frac{U_m}{\sqrt2}e^{j\psi_u}\)
\(i(t)=I_msin{(}\omega t+\psi_i)\rightarrow\frac{I_m}{\sqrt2}e^{j\psi_i}\)
- Zastosowanie reprezentacji elementów poprzez ich impedancje zespolone.
- Zastosowanie praw Kirchoffa dla wartości symbolicznych.
- Rozwiązanie układu równań algebraicznych zespolonych.
- Ewentualnie (w miarę potrzeb) przedstawienie rozwiązania w postaci czasowej (odwrotna operacja) do wykonanej w punkcie pierwszym).
2.4. Wykres wektorowy obwodu
W przypadku analizy obwodów RLC w stanie ustalonym ważnym pojęciem jest wykres wektorowy, zwany również wykresem wskazowym, przedstawiający w sposób graficzny zależności między poszczególnymi wektorami prądu i napięcia w obwodzie. Jak wiadomo każdej liczbie zespolonej można przyporządkować reprezentację geometryczną w postaci odpowiedniej zależności wektorowej przedstawionej na płaszczyźnie, w której oś pozioma odpowiada części rzeczywistej a oś pionowa części urojonej liczby zespolonej. Konstruując wykres należy pamiętać, że pomnożenie wektora przez operator j jest równoważne obrotowi tego wektora o kąt 90 stopni przeciwnie do ruchu wskazówek zegara gdyż operator j jest równy \(e^{j90^\circ}\). Podobnie pomnożenie wektora przez operator -j jest równoważne jego obrotowi o kąt 90 stopni zgodnie z ruchem wskazówek zegara gdyż operator -j jest równy \(e^{-j90^\circ}\) . Pomnożenie wektora przez liczbę rzeczywistą nie zmienia pozycji wektora w przestrzeni o ile jest to liczba dodatnia lub zmienia zwrot wektora o \(180^o\) jeśli liczba ta jest ujemna.
Z zależności prądowo-napięciowych dla rezystora jest oczywiste, że
| \(U_R=RI_R\) | (2.26) |
co wobec rzeczywistych, dodatnich wartości R oznacza, że napięcie na rezystorze jest w fazie z prądem tego rezystora. Dla cewki obowiązuje
| \(U_L=j\omega LI_L=\omega LI_Le^{j90^o}\) | (2.27) |
co oznacza, że napięcie na cewce wyprzedza prąd o kąt \(90^\circ\). Podobnie napięcie na kondensatorze opóźnia się względem swojego prądu o kąt \(90^\circ\), gdyż
| \(U_C=-j\frac{1}{\omega C}I_C=\frac{1}{\omega C}I_Ce^{-j90^o}\) | (2.28) |
Na rys. 2.3 przedstawiono wykresy wektorowe dla rezystora, cewki i kondensatora z zaznaczeniem przesunięć kątowych między wektorami prądu i napięcia.
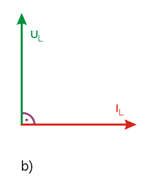
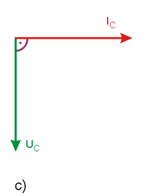
Rys. 2.3. Wykresy wektorowe dla a) rezystora, b) cewki, c) kondensatora
Przedstawione powyżej zasady konstruowania przesunięć kątowych między wektorami prądu i napięcia umożliwiają podanie ogólnych zasad postępowania przy konstruowaniu wykresu wektorowego dla dowolnego połączenia elementów obwodu RLC.
Wykres wektorowy z definicji uwzględnia przede wszystkim przesunięcia kątowe między poszczególnymi wektorami. Relacje ilościowe (długości) poszczególnych wektorów są mniej istotne i zwykle uwzględniane w sposób jedynie przybliżony. Wykres rozpoczyna się zwykle od końca obwodu (gałęzi najdalej położonej od źródła). Jeśli gałąź jest połączeniem szeregowym elementów rozpoczynamy od prądu tej gałęzi, a w przypadku połączenia równoległego – od napięcia. Następnie rysuje się na wykresie na przemian napięcia i prądy kolejnych gałęzi, dochodząc w ten sposób do źródła. Budowę wykresu kończy się w momencie dojścia do prądu i napięcia źródłowego obwodu.
Narysować wykres wektorowy prądów i napięć dla obwodu RLC o strukturze przedstawionej na rys. 2.4.
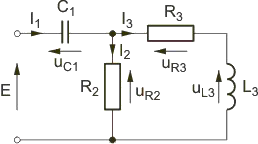
Rys. 2.4. Schemat obwodu RLC do przykładu 2.1
Rozwiązanie
Na rys. 2.5 przedstawiono wykres wektorowy prądów i napięć w obwodzie RLC z rys. 2.4.
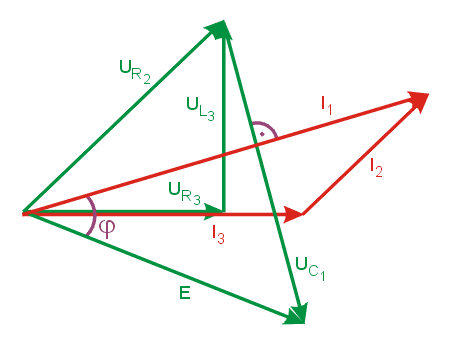
Rys. 2.5. Wykres wektorowy prądów i napięć dla obwodu z rys. 2.4
Sporządzanie wykresu rozpoczyna się od prądu I3 dobudowując wektory napięć i prądów gałęzi przesuwając się w stronę źródła, kolejno: \(U_{R_3},U_{L_3},U_{R_2},I_2,I_1,U_{C_1},E\). Przy założonych wielkościach wektorów obwód ma charakter pojemnościowy, gdyż napięcie wypadkowe E opóźnia się względem odpowiadającego mu prądu \(I_1\).
Położenie wektora prądu źródłowego względem napięcia źródłowego decyduje o charakterze obwodu. Jeśli napięcie wypadkowe (źródłowe) wyprzedza prąd wypadkowy (źródłowy) lub inaczej mówiąc prąd opóźnia się względem napięcia - obwód ma charakter indukcyjny. Jeśli natomiast napięcie opóźnia się względem prądu (lub prąd wyprzedza napięcie) - mówimy o charakterze pojemnościowym obwodu. Jeśli natomiast wektory prądu i napięcia są ze sobą w fazie mówimy, że obwód ma charakter rezystancyjny.
2.5. Zjawisko rezonansu w obwodzie
Zjawiskiem rezonansu nazywamy taki stan obwodu RLC, w którym prąd i napięcie są ze sobą w fazie. W stanie rezonansu przesunięcie fazowe prądu i napięcia jest zerowe, co oznacza, że argument impedancji lub admitancji zespolonej obwodu jest także równy zeru. Rezonans wystąpić może w dowolnej konfiguracji elementów RLC, tym nie mniej bada się szczególne połączenia elementów prowadzące do tego zjawiska. Rezonans występujący w obwodzie, w którym elementy R, L, C są połączone szeregowo nazywamy rezonansem napięć lub rezonansem szeregowym. W przypadku, gdy rezonans dotyczy obwodu równoległego R, L, C taki rezonans nazywamy rezonansem prądów lub rezonansem równoległym.
2.6. Rezonans szeregowy
W rezonansie szeregowym RLC zjawisko rezonansu wymaga, aby reaktancja wypadkowa obwodu była równa zeru (impedancja całkowita jest wówczas wartością rzeczywistą pomimo istnienia cewek i kondensatorów w obwodzie). W rezonansie równoległym warunek rezonansu wymaga, aby część urojona admitancji była równa zeru. Częstotliwość, przy której część urojona impedancji lub admitancji obwodu znika jest nazywana częstotliwością rezonansową.
Przyjmijmy do analizy obwód szeregowy R, L, C przedstawiony na rys. 2.6.
Rys. 2.6. Obwód rezonansowy szeregowy RLC
zasilany napięciem sinusoidalnie zmiennym o wartości skutecznej zespolonej U i pulsacji \(\omega=2\pi f\). Przy zastosowaniu metody symbolicznej w analizie tego obwodu można napisać następujące równanie napięciowe Kirchhoffa
| \(U=U_R+U_L+U_C=RI+jX_LI-jX_CI=I\left[R+j(X_L-X_C)\right]\) | (2.29) |
Zjawiskiem rezonansu nazywamy taki stan obwodu RLC, w którym prąd i napięcie są ze sobą w fazie. Osiągnie się to, jeśli część urojona powyższej zależności będzie równa zeru, czyli
\(X_L=X_C\)
Uwzględniając, że \(X_L=\omega L\) oraz \(X_C=1/\omega C\) z powyższego warunku otrzymuje się wzór określający pulsację rezonansową \(\omega_r\) w postaci
| \(\omega_r=\frac{1}{\sqrt{LC}}\) | (2.30a) |
Częstotliwość rezonansowa obwodu wynosi zatem
| \(f_r=\frac{1}{2\pi\sqrt{LC}}\) | (2.30b) |
Równość reaktancji indukcyjnej i pojemnościowej oznacza, że w stanie rezonansu napięcia na cewce i kondensatorze są równe co do modułu ale przeciwnie skierowane, czyli
| \(\left|U_L\right|=-\left|U_C\right|\) | (2.31) |
Zmiana częstotliwości zmienia oczywiście relację między napięciami na tych elementach reaktancyjnych (przeskalowanie wartości). Dla częstotliwości mniejszych niż rezonansowa napięcie na kondensatorze jest większe niż na cewce (przy mniejszej częstotliwości moduł impedancji kondensatora jest większy), a przy częstotliwościach większych niż rezonansowa napięcie na cewce większe niż na kondensatorze (moduł impedancji cewki rośnie wraz ze wzrostem częstotliwości a moduł impedancji kondensatora maleje). Na rys. 2.7 przedstawiono wykresy wektorowe prądu i napięć w obwodzie szeregowym RLC dla częstotliwości mniejszych niż rezonansowa (rys. 2.7a), dla częstotliwości rezonansowej (rys. 2.7b) oraz dla częstotliwości większych niż rezonansowa (rys. 2.7c).
| a) | b) | c) |
Rys. 2.7. Wykresy wektorowe obwodu rezonansowego RLC: a) stan przed rezonansem,
b) stan rezonansu, c) stan po rezonansie
Z przesunięć kątowych między wektorami widoczne jest, że przed rezonansem obwód szeregowy RLC ma charakter pojemnościowy, w czasie rezonansu – rezystancyjny, a dla częstotliwości większych niż rezonansowa – indukcyjny.
Ważnym parametrem obwodu rezonansowego jest dobroć Q określana zwykle w punkcie rezonansowym (dla częstotliwości rezonansowej). W obwodzie szeregowym RLC dobrocią nazywamy stosunek wartości skutecznej napięcia na elemencie reaktancyjnym (kondensatorze lub cewce) do wartości skutecznej napięcia na elemencie rezystancyjnym w czasie rezonansu. Stąd wartość dobroci może być wyrażona wzorem
| \(Q=\frac{\left|U_L\right|}{\left|U_R\right|}=\frac{\left|U_C\right|}{\left|U_R\right|}=\frac{\omega_rL}{R}=\frac{1}{\omega_rRC}\) | (2.32) |
Po uwzględnieniu wzoru na pulsację rezonansową, dobroć Q można wyrazić w jednoznacznej postaci uzależnionej wyłącznie od parametrów obwodu RLC
| \(Q=\frac{\sqrt{\frac{L}{C}}}{R}\) | (2.33) |
Wielkość występująca w liczniku nazywana jest rezystancją charakterystyczną r
| \(\rho=\sqrt{\frac{L}{C}}\) | (2.34) |
Rezystancja charakterystyczna obwodu rezonansowego szeregowego RLC jest uzależniona wyłącznie od wartości indukcyjności i pojemności.
Charakterystykami częstotliwościowymi obwodu rezonansowego nazywać będziemy zależność prądu i napięć od częstotliwości (pulsacji). Dla otrzymania charakterystyk częstotliwościowych z równania (2.29) wyznaczmy prąd I jako funkcję pulsacji
| \(I\left(\omega\right)=\frac{U}{R+j\omega L-j1/\omega C}\) | (2.35) |
Przepisując powyższą zależność zespoloną w postaci wykładniczej otrzymujemy wzór
| \(I\left(\omega\right)=\left|I(\omega)\right|e^{j\phi(\omega)}\) | (2.36) |
w którym \(\left|I(\omega)\right|\) oznacza moduł prądu a \(\phi(\omega)\) - fazę uzależnioną od częstotliwości napięcia zasilającego. Wielkości te opisane są następująco
| \(\left|I(\omega)\right|=\frac{\left|U\right|}{\sqrt{R^2+\left(\omega L-1/\omega C\right)^2}}\) | (2.37) |
| \(\left|I(\omega)\right|=\frac{\left|U\right|}{\sqrt{R^2+\left(\omega L-1/\omega C\right)^2}}\) | (2.38) |
Zależność modułu od częstotliwości (pulsacji) nazywamy charakterystyką amplitudową rezonansu a zależność fazy od częstotliwości (pulsacji) – charakterystyką fazową. Na rys2.8a przedstawiono charakterystykę modułu prądu a na rys. 2.8b – fazy prądu w funkcji pulsacji \(\omega\) .
Rys. 2.8. Charakterystyki częstotliwościowe prądu w obwodzie rezonansowym:
a) charakterystyka amplitudowa, b) charakterystyka fazowa
Wartości elementów symulowanego obwodu były równe: L=1H, C=1F, R=1,8
Wraz ze zmianą prądu zmieniają się również napięcia na pozostałych elementach obwodu RLC. Dla wyznaczenia tych zależności można wykorzystać prawo Ohma, zgodnie z którym przy zastosowaniu podejścia symbolicznego otrzymuje się
- dla indukcyjności
| \(U_L(\omega)=j\omega LI(\omega)\) | (2.39) |
- dla pojemności
| \(U_C(\omega)=-j\frac{I(\omega)}{\omega C}\) | (2.40) |
Podstawiając do powyższych zależności wzór określający prąd można otrzymać wyrażenia na moduły i fazy napięcia na cewce i kondensatorze. Charakterystyki amplitudowe tych napięć są wyrażone w postaci
| \(\left|U_L(\omega)\right|=\frac{\left|U\right|\omega L}{\sqrt{R^2+\left(\omega L-1/\omega C\right)^2}}\) | (2.41 |
| \(\left|U_C(\omega)\right|=\frac{\left|U\right|}{\omega C\sqrt{R^2+\left(\omega L-1/\omega C\right)^2}}\) | (2.42) |
Na rys. 2.9 przedstawiono przykładowe charakterystyki amplitudowe napięcia na cewce i kondensatorze w obwodzie RLC o podanych wcześniej parametrach przy pulsacji rezonansowej równej jeden i dobroci obwodu
Rys. 2.9. Charakterystyki amplitudowe napięcia na cewce i kondensatorze
Jak widać dla częstotliwości rezonansowej obwodu napięcia na reaktancjach są sobie równe.
Charakterystyki fazowe napięć na cewce i kondensatorze, jak wynika ze wzorów (2.39) i (2.40) różnią się od charakterystyki fazowej prądu tylko o wartość
- charakterystyka fazowa napięcia cewki
| \(\phi_L(\omega)=\frac{\pi}{2}-arctg{\frac{\omega L-1/\omega C}{R}}\) | (2.43) |
- charakterystyka fazowa napięcia kondensatora
| \(\phi_C(\omega)=-\frac{\pi}{2}-arctg{\frac{\omega L-1/\omega C}{R}}\) | (2.44) |
Kształt charakterystyk fazowych napięcia na cewce i kondensatorze jest identyczny z charakterystyką fazową prądu. Jedynym wyjątkiem jest przesunięcie tych charakterystyk w osi pionowej o wartość kąta równą \(\pm90^o\) .
Ogromny wpływ na charakterystyki częstotliwościowe zarówno amplitudową jak i fazową wywiera dobroć obwodu. Im wyższa jest dobroć tym charakterystyka prądu w funkcji częstotliwości jest bardziej stroma. Zmniejszenie dobroci powoduje spłaszczenie charakterystyki prądu (gorsza selektywność obwodu rezonansowego).
Rys. 2.10. Ilustracja wpływu dobroci na charakterystykę amplitudową prądu
Rys. 2.10 przedstawia wpływ dobroci na charakterystykę amplitudową prądu przy stałej wartości amplitudy napięcia zasilającego i zmiennej rezystancji, regulującej dobroć obwodu. Im większa dobroć tym charakterystyka amplitudowa jest bardziej stroma.
Na rys. 2.11 zilustrowano wpływ dobroci na charakterystyki amplitudowe napięcia cewki i kondensatora dla tych samych wartości częstotliwości rezonansowej i dobroci jak na rys. 2.10.
Rys. 2.11. Charakterystyki amplitudowe napięcia na cewce i kondensatorze
Zaobserwować można pojawienie się maksimum w charakterystyce zarówno napięcia cewki jak i kondensatora. Łatwo można udowodnić, że punkt maksymalny obu charakterystyk pojawia się jedynie przy dobroci obwodu większej niż \(\frac{1}{\sqrt2}\) . Dobroć \(Q=\frac{1}{\sqrt2}\) odpowiada najbardziej płaskiemu kształtowi charakterystyk amplitudowych.
2.7. Rezonans równoległy
Rezonans prądów zwany również rezonansem równoległym może wystąpić w obwodzie zawierającym połączenie równoległe elementów RLC. Istnieje wiele struktur obwodów, w których może powstać rezonans prądów. Warunkiem jest pojawienie się równoległego połączenia cewki i kondensatora, przy czym zarówno cewka jak i kondensator może być w układzie połączeń z innymi elementami rezystancyjnymi. Na rys. 2.12 przedstawiono przykładowy najprostszy obwód rezonansu równoległego RLC.
Rys. 2.12 Obwód rezonansowy równoległy RLC
Podobnie jak w przypadku obwodu szeregowego przyjmiemy wymuszenie sinusoidalne o zmiennej częstotliwości, ale tym razem założymy je w postaci źródła prądowego \(i(t)=I_msin{(}\omega t)\) . Wykorzystując w opisie obwodu metodę symboliczną równanie prądowe Kirchhoffa dla tego obwodu przyjmie postać
| \(I=I_R+I_L+I_C=GU+j\omega CU-\frac{jU}{\omega L}=U\left[G+j\left(\omega C-\frac{1}{\omega L}\right)\right]\) | (2.45) |
Warunkiem rezonansu równoległego jest przyjęcie przez kąt fazowy między prądem I oraz napięciem U wartości równej zeru. Nastąpi to wtedy, gdy część urojona zależności (2.45) przyjmie wartość zerową, czyli gdy
| \(\omega C=\frac{1}{\omega L}\rightarrow\omega=\frac{1}{\sqrt{LC}}\) | (2.46) |
Warunek powyższy będzie spełniony, gdy częstotliwość zasilania przyjmie wartość częstotliwości rezonansowej określonej zależnością
| \(f_r=\frac{1}{2\pi\sqrt{LC}}\) | (2.47) |
Jak widać częstotliwość rezonansowa w obwodzie równoległym z rys. 2.12 jest określona identycznym wzorem jak w obwodzie szeregowym RLC. W odróżnieniu od obwodu szeregowego w obwodzie równoległym dobrocią nazywamy stosunek prądu \(I_L\) lub \(I_C\) (są sobie równe w chwili rezonansu) do prądu \(I_R\) w elemencie rezystancyjnym \(I_R\)
| \(Q=\frac{| I_{L}| }{| I_{R}| } =\frac{| I_{C}| }{| I_{R}| } =\frac{\omega _{r} C}{G} =\frac{1}{\omega _{r} GL}\) | (2.48) |
Po uwzględnieniu \(G=1/R\) i wzoru (2.47) na częstotliwość rezonansową otrzymuje się relację określającą dobroć równoległego obwodu rezonansowego RLC o strukturze przedstawionej na rys. 2.12 w postaci
| \(Q=\frac{R}{\sqrt{\frac{L}{C}}}\) | (2.49) |
Tym razem dobroć obwodu jest wprost proporcjonalna do wartości rezystancji a odwrotnie proporcjonalna do rezystancji charakterystycznej. Dobroć obwodu wzrasta więc ze wzrostem wartości rezystancji, odwrotnie niż to miało miejsce w obwodzie rezonansu szeregowego (przy większej rezystancji równoległej płynie przez nią mniejszy prąd upływnościowy).
Dobroć Q, podobnie jak w obwodzie rezonansu szeregowego, ma ogromny wpływ na charakterystyki częstotliwościowe obwodu RLC. Zauważmy, że z równania (2.45) można wyznaczyć napięcie na elementach R, L, C w postaci
| \(U\left(\omega\right)=\frac{I}{G+j\omega C-j1/\omega L}=\left|U(\omega)\right|e^{j\phi(\omega)}\) | (2.50) |
w którym \(\left|U(\omega)\right|\) oznacza moduł napięcia a \(\phi(\omega)\) - fazę uzależnioną od częstotliwości prądu zasilającego. Wielkości te opisane są następującą funkcją
| \(\left|U(\omega)\right|=\frac{\left|I\right|}{\sqrt{G^2+\left(\omega C-1/\omega L\right)^2}}\) | (2.51) |
| \(\phi(\omega)=-arctg{\frac{\omega C-1/\omega L}{G}}\) | (2.52) |
Na rys. 2.13 przedstawiono charakterystykę modułu napięcia (charakterystykę amplitudową) i wykres fazy napięcia (charakterystykę fazową) w funkcji pulsacji
Rys. 2.13 Charakterystyka amplitudowa (powyżej) i fazowa (ponizej) napięcia w obwodzie równoległym RLC
W punkcie rezonansowym (częstotliwość zasilania równa częstotliwości rezonansowej) charakterystyka amplitudowa przyjmuje wartość maksymalną a faza wartość zerową. Charakterystyki te są analogiczne do charakterystyk dla obwodu szeregowego przy uwzględnieniu formalnych zmian występujących we wzorach (prąd w obwodzie szeregowym odpowiada napięciu na połączeniu równoległym elementów). Zmiana kształtu charakterystyk częstotliwościowych obwodu równoległego na skutek zmian dobroci jest również identyczna jak miało to miejsce w obwodzie szeregowym RLC. Odpowiednikiem napięcia na elementach L i C w obwodzie szeregowym jest prąd tych elementów w obwodzie równoległym. Zachowanie się tych charakterystyk w funkcji pulsacji wynika z prawa Ohma dla cewki i kondensatora, to jest
| \(I_C(\omega)=j\omega CU(\omega)\) | (2.53) |
oraz
| \(I_L(\omega)=-\frac{jU(\omega)}{\omega L}\) | (2.54) |
Ograniczając się jedynie do charakterystyk amplitudowych można łatwo wykazać, że charakterystyki te opisują się następującymi wzorami
| \(\left|I_C(\omega)\right|=\frac{\left|I\right|\omega C}{\sqrt{G^2+\left(\omega C-\frac{1}{\omega L}\right)^2}}\) | (2.55) |
| \(\left|I_L(\omega)\right|=\frac{\left|I\right|}{\omega L\sqrt{G^2+\left(\omega C-\frac{1}{\omega L}\right)^2}}\) | (2.56) |
Na rys. 2.14 przedstawiono charakterystyki amplitudowe prądu cewki i kondensatora w funkcji pulsacji dla dobroci \(Q<\frac{1}{\sqrt2}\) wynikające z relacji (2.55) i (2.56).
Rys. 2.14 Charakterystyki amplitudowe prądu cewki i kondensatora
Zmiana dobroci obwodu wpływa w zasadniczy sposób na przebieg tych charakterystyk. Można łatwo udowodnić, że dla dobroci \(Q>\frac{1}{\sqrt2}\) pojawiają się punkty ekstremalne (maksima) w obu charakterystykach, podobnie jak przy rezonansie szeregowym, przy czym występuje przesunięcie tych maksimów względem punktu rezonansowego. Przesunięcie to maleje wraz ze zwiększaniem się dobroci. Przy dobroci \(Q\le\frac{1}{\sqrt2}\) punkty ekstremalne w obu charakterystykach nie występują a przebieg charakterystyk amplitudowych staje się monotoniczny.
Rezonans równoległy podobnie jak szeregowy ma głównie zastosowanie w układach filtrów i generatorów, gdzie pełni rolę układu przepuszczającego lub wzmacniającego sygnały w określonym zakresie częstotliwości i tłumiącego w pozostałym zakresie.
3. Moce w obwodach RLC przy wymuszeniu sinusoidalnym
Jednym z najważniejszych pojęć w elektrotechnice jest moc elektryczna. Jest ona ściśle związana ze zjawiskami energetycznymi zachodzącymi w obwodzie. Przepływ prądu w obwodzie jest związany z energią wydzielaną lub gromadzoną na poszczególnych elementach. Wielkościom prądu i napięcia przyporządkować można różne rodzaje mocy. W obwodach elektrycznych o przebiegach sinusoidalnych definiuje się cztery rodzaje mocy: moc chwilową, czynną, bierną i pozorną zespoloną.
Wykład trzeci poświęcony jest zagadnieniom związanym z obliczaniem mocy chwilowej p(t), mocy czynnej P, mocy biernej Q oraz mocy pozornej zespolonej S. Poznamy wzory wiążące poszczególne rodzaje mocy z prądami i napięciami w obwodzie RLC przy wymuszeniu sinusoidalnym w stanie ustalonym. Podane zostaną wzory wyrażające energię zgromadzoną w cewce i kondensatorze. Ostatnim fragmentem wykładu są zagadnienia dopasowania odbiornika do źródła rzeczywistego o niezerowej impedancji wewnętrznej.
3.1. Moc chwilowa
Oznaczmy wartość chwilową napięcia i prądu gałęzi odpowiednio przez \(u(t)=U_msin{(}\omega t)\) oraz \(i(t)=I_msin{(}\omega t-\phi)\). Dla uproszczenie przyjęto fazę początkową napięcia równą zeru.
Moc chwilowa p(t), jako jedyna z mocy jest funkcją czasu i definiuje się ją w postaci iloczynu wartości chwilowych prądu \(i(t)\) oraz napięcia \(u(t)\) w obwodzie
| \(p(t)=u(t)i(t)\) | (3.1) |
Przy wymuszeniu sinusoidalnym moc chwilowa opisana jest wzorem
|
\(p(t)=u(t)i(t)=U_mI_msin{(}\omega t)sin{(}\omega t-\phi)=\frac{U_mI_m}{2}\left[cos{\phi}-cos{(}2\omega t-\phi)\right]=\\ =\left|U\right|\left|I\right|[cos{-}cos{(}2\omega t-\phi)]\) |
(3.2) |
3.2. Moc czynna
Moc czynną definiuje się jako wartość średnią za okres z mocy chwilowej, to jest
| \(P=\frac{1}{T}\int_{t_0}^{t_0+T}{p(t)dt}\) | (3.3) |
Podstawiając do powyższego wzoru funkcję określającą moc chwilową w obwodzie, po wykonaniu operacji całkowania otrzymuje się
| \(P=\left|U\right|\left|I\right|cos{\phi}\) | (3.4) |
Moc czynna w obwodzie o wymuszeniu sinusoidalnym jest więc wielkością stałą (niezależną od czasu) równą iloczynowi modułów wartości skutecznych napięcia i prądu oraz cosinusa kąta przesunięcia fazowego między wektorem napięcia i prądu. Współczynnik \(cos{\phi}\) odgrywa ogromną rolę w praktyce i nosi specjalną nazwę współczynnika mocy.
Moc czynna stanowi składową stałą mocy chwilowej. Jest ona nieujemna dla obwodu RLC a w granicznym przypadku przy \( \phi=\pm\pi/2\mathrm{\ \ \ }\rightarrow\mathrm{\ \ \ }\mathrm{P}_L=P_C=0\) jest równa zeru. Moc czynna osiąga wartość największą \(P=\left|U\right|\left|I\right| \)gdy \(\phi=0\), to znaczy gdy odbiornik ma charakter rezystancyjny, \(cos{\phi}=1\). Wartość najmniejszą (P=0) moc osiąga w przypadku granicznym, gdy \(\phi=\pm\pi/2\), to znaczy gdy odbiornikiem jest cewka idealna lub kondensator idealny dla których \(cos{\phi}=0\). Oznacza to, że na elementach reaktancyjnych nie wydziela się moc czynna.
Z przytoczonych rozważań wynika, moc czynną wydzielaną w rezystorze można opisać następującymi wzorami
| \(P=\left|U\right|\left|I\right|cos{\phi}=R\left|I\right|^2=G\left|U\right|^2\) | (3.5) |
w których prąd I oraz napięcie U odpowiadają rezystorowi R. Jednostką mocy czynnej jest wat (W), przy czym 1W=1AV. W praktyce stosuje się również wielokrotności wata w postaci kilowata (1kW=1000W) lub megawata (1MW=106W) oraz wartości ułamkowe, np. miliwat (mW) lub mikrowat (
Do pomiaru mocy czynnej służy watomierz. Klasyczny watomierz jest przyrządem pomiarowym posiadającym cewkę prądową (o impedancji wewnętrznej bliskiej zeru) do pomiaru prądu gałęziowego obwodu i cewkę napięciową (o impedancji wewnętrznej bliskiej nieskończoności) do pomiaru napięcia między punktami obwodu, dla którego mierzymy moc czynną. Początki uzwojeń obu cewek oznaczać będziemy na schematach przy pomocy gwiazdek. Pozycja znaku gwiazdki przy cewce prądowej wskazuje kierunek prądu Iw watomierza przyjęty za dodatni (prąd płynie od gwiazdki do watomierza). W przypadku cewki napięciowej pozycja gwiazdki wskazuje przyjęty kierunek wyższego potencjału (napięcia Uw) obwodu. Wskazanie watomierza jest wówczas określone wzorem (3.4), które przy naszych oznaczeniach prądu i napięcia watomierza przyjmą postać \(P=\left|U_w\right|\left|I_w\right|cos{\phi}\). Przyjmując założenie idealizujące, że impedancja cewki prądowej watomierza jest równa zeru a cewki napięciowej równa nieskończoności watomierz nie ma żadnego wpływu na rozpływy prądów i rozkłady napięć w badanym obwodzie elektrycznym.
3.3. Moc bierna
W obwodach elektrycznych prądu sinusoidalnego definiuje się trzecią wielkość energetyczną będącą iloczynem napięcia i prądu oraz sinusa kąta przesunięcia fazowego między nimi. Wielkość ta oznaczana jest literą Q i nazywana mocą bierną
| \(Q=\left|U\right|\left|I\right|sin{\phi}\) | (3.6) |
Jednostką mocy biernej jest war (var) będący skrótem nazwy woltamper reaktywny.
W przypadku rezystora, dla którego przesunięcie fazowe jest równe zeru (\(\phi=0\mathrm{\ \ \ }\rightarrow\mathrm{\ \ \ }\mathrm{Q}_R=0\)) moc bierna jest zerowa Moc bierna może się więc wydzielać jedynie na elementach reaktancyjnych, gdyż tylko dla nich przesunięcie fazowe prądu i napięcia jest różne od zera. Przesunięcie fazowe prądu i napięcia na elementach reaktancyjnych (cewce i kondensatorze) przyjmuje wartość +90 dla cewki oraz -90 dla kondensatora, co oznacza, że sinus kąta jest odpowiednio równy równy +1 dla cewki (moc bierna cewki jest uważana za dodatnią) oraz –1 dla kondensatora (moc bierna kondensatora jest uważana za ujemną). Stąd przy uwzględnieniu znaku wzór na moc bierną elementów reaktancyjnych o reaktancji X może być przedstawiony w trzech równorzędnych postaciach
| \(Q_X=\pm\left|U\right|\left|I\right|sin{\phi}=\pm X\left|I\right|^2=\pm\frac{1}{X}\left|U\right|^2\) | (3.7) |
W ogólności kąt przesunięcia fazowego \(\phi\) uważa się za dodatni dla obwodów o charakterze indukcyjnym (napięcie wyprzedza prąd) a za ujemny dla obwodów o charakterze pojemnościowym (napięcie opóźnia się względem prądu). Moc bierna obwodów o charakterze indukcyjnym jest w sumie mocą indukcyjną, kojarzona z wartością dodatnią a moc bierna obwodów o charakterze pojemnościowym jest w sumie mocą pojemnościową i kojarzoną z wartością ujemną.
3.4. Moc pozorna zespolona
Czwartym rodzajem mocy wprowadzanym w obwodach elektrycznych jest tak zwana moc pozorna zespolona. Jest ona proporcjonalna do wartości skutecznych prądu i napięcia, i oznaczana literą S. Moc pozorna zespolona definiowana jest formalnie jako liczba zespolona w postaci iloczynu wartości skutecznej zespolonej napięcia U i wartości skutecznej sprzężonej prądu I
| \(S=UI^\ast=P+jQ\) | (3.8) |
Tak zdefiniowana moc pozorna zespolona przedstawia sobą sumę mocy czynnej (część rzeczywista S) oraz mocy biernej (część urojona S), stąd
| \(S=P+jQ\) | (3.9) |
Biorąc pod uwagę, że operator j oznacza przesunięcie wektora o kąt \(90^\circ\), ostatniej zależności na moc pozorną przyporządkować można wykres wektorowy mocy, tzw. trójkąt mocy przedstawiony na rys. 3.1.
| a) | b) |
Rys. 3.1. Wykres wektorowy mocy dla obwodu a) o charakterze indukcyjnym, b) o charakterze pojemnościowym
Zależność na moc pozorną zespoloną można przedstawić również w postaci wykładniczej \(S=\left|S\right|e^{j\phi}\). W zależności tej \(\left|S\right|\) wyraża moduł mocy pozornej zespolonej, zwany również mocą pozorną która może być wyrażona w postaci iloczynu modułów wartości skutecznych prądu i napięcia
| \(\left|S\right|=\left|U\right|\left|I\right|=\sqrt{P^2+Q^2}\) | (3.10) |
Z wykresu wektorowego obwodu przedstawionego na rys. 3.1 możliwe jest wyznaczenie współczynnika mocy. Mianowicie
| \(cos{\phi}=\frac{P}{\left|S\right|}\) | (3.11) |
Wartość współczynnika mocy wyznaczona z powyższej zależności jest identyczna z wartością wynikającą z relacji prądowo-napięciowych zachodzących dla wielkości bramowych (zewnętrznych) obwodu. Dla ułatwienia korzystania z pojęć mocy zestawiono poniżej najważniejsze postacie wzorów na moc czynną, bierną i pozorną w poszczególnych elementach obwodu
- Moc pozorna zespolona
| \(S=UI^\ast=P+⥂jQ \) | (3.12) |
- Moc czynna
| \(P=Re{(}S)=\left|U\right|\left|I\right|cos{\phi}=\left|I_R\right|^2R=\frac{\left|U_R\right|^2}{R}\) | (3.13) |
- Moc bierna
| \(Q=Im{(}S)=\left|U\right|\left|I\right|sin{\phi}=\pm\left|I_X\right|^2X=\pm\frac{\left|U_X\right|^2}{X}\) | (3.14) |
Znak plus dotyczy mocy biernej cewki a minus kondensatora. W przypadku źródeł należy korzystać ze wzoru (3.12) na moc zespoloną pozorną S.
3.5. Bilans mocy
W obwodzie elektrycznym, jak w każdym układzie fizycznym obowiązuje prawo zachowania energii. W przypadku obwodów prawo to przekształca się w tak zwane prawo bilansu mocy.
Bilans mocy
Jeśli całkowitą moc pozorną zespoloną wytworzoną przez źródło (lub wiele źródeł występujących w obwodzie) oznaczymy przez Sg a sumaryczną moc pozorną zespoloną wydzieloną w elementach odbiornika przez So, to biorąc pod uwagę prawo zachowania energii obie moce muszą być sobie równe, to znaczy Sg=So. Jest to tak zwana zasada bilansu mocy w obwodach elektrycznych.
W tak sformułowanej zasadzie bilansu mocy przyjmuje się standardowo, że zwroty prądów i napięć w elementach odbiornikowych są przeciwne sobie a w elementach źródłowych takie same. Jeśli przyjmiemy ujednoliconą zasadę znakowania prądów i napięć na elementach obwodu, zakładającą, że niezależnie od rodzaju elementu zwroty prądu i napięcia na gałęzi są przeciwne sobie, to zasadę bilansu mocy można sformułować w ten sposób, że suma mocy pozornej zespolonej liczonej po wszystkich elementach w obwodzie elektrycznym jest równa zeru, Sg+So=0.
Dla zilustrowania wprowadzonych tu pojęć mocy oraz zasady bilansowania się mocy rozpatrzymy przykład obwodu przedstawionego na rys. 3.2.
Niech dany będzie obwód RLC o strukturze przedstawionej na rys. 3.2 zasilany z sinusoidalnego źródła napięcia \((t)=100\sqrt2sin{(}\omega t+45^\circ)\) V przy \(\omega=1\frac{rad}{s}\) . Wartości elementów obwodu są następujące:
Rys. 3.2. Schemat obwodu do przykładu 3.1
Należy wyznaczyć wartości skuteczne zespolone prądów i napięć elementów oraz moce w obwodzie.
Rozwiązanie
Wartości zespolone impedancji i napięcia wymuszającego w obwodzie przy danych wartościach elementów są równe:\(Z_L=j\omega L=j1\), \(Z_C=-j1/\omega C=-j2\) , \(E=100e^{j45^o}\). Impedancja zastępcza połączenia równoległego L i R równa się \(Z_{RL}=\frac{RZ_L}{R+Z_L}=0.707e^{j45^o}\) . Impedancja zastępcza połączenia szeregowego C i \(Z_{RL}\) jest równa \(Z=Z_C+Z_{RL}=0,5+j0,5-j2=1,58e^{-j71,6^o}\).
Zgodnie z prawem Ohma prąd I w obwodzie jest równy
\(I_C=\frac{E}{Z}=\frac{100e^{j45^o}}{1,58e^{-j71,6^o}}=63,3e^{j116,6^o}\)
Napięcia na poszczególnych elementach obwodu dane są w postaci
\(U_C=Z_CI_C=126,6e^{j26,6^o}\)
\(U_{RL}=Z_{RL}I_C=44,72e^{j161,6^o}\)
Prądy cewki i rezystora obliczone z prawa Ohma równają się
\(I_L=\frac{U_{RL}}{Z_L}=44,72e^{j71,6^o}\)
\(I_R=\frac{U_{RL}}{R}=44,72e^{j161.6^o}\)
Na rys. 3.3 przedstawiono wykres wektorowy prądów i napięć w obwodzie.
Rys. 3.3. Wykres wektorowy prądów i napięć w obwodzie z rys. 3.2
Poszczególne rodzaje mocy wydzielonej w obwodzie równają się:
- Moc pozorna zespolona wydawana przez źródło
\(S=E\cdot{I_C}^\ast=(2000-j6000)V\cdot A\)
- Moc czynna rezystora
\(P_R=\left|I_R\right|^2R=2000W\)
- Moc bierna cewki i kondensatora
\(Q_L=Im{(}U_{RL}\cdot I_L^\ast)=2000var\)
\(Q_C=Im{(}U_C\cdot I_C^\ast)=-8000var\)
Całkowita moc bierna wydzielona na cewce i kondensatorze równa się
\(Q=Q_L+Q_C=-6000var\)
Moc wydzielona na rezystorze oraz cewce i kondensatorze równa się dokładnie mocy dostarczonej przez źródło. Bilans mocy generowanej przez źródło i mocy wydzielonej w odbiorniku jest zatem równy zeru.
Załączony program „Rozpływ prądów w obwodzie AC – obwód 1” pozwala obserwować wartości prądów, napięć i mocy pozornej zespolonej w poszczególnych elementach R, L, C obwodu zasilanych ze źródła napięciowego typu sinusoidalnego o zadanej wartości skutecznej Esk, pulsacji ω i fazie początkowej φ. Użytkownik może zmieniać wartości zarówno parametrów źródła napięciowego jak i wartości poszczególnych elementów. Program wyświetla przebiegi czasowe napięcia zasilającego oraz prądów i napięć poszczególnych elementów jak również mocy chwilowej. Warto zwrócić uwagę na fazy prądu cewki i kondensatora. Przy identycznym napięciu panującym na połączeniu równoległym tych elementów fazy tych prądów różnią się o 180o. Każda zmiana wartości jakiegokolwiek elementu powoduje automatyczną zmianę wartości rozwiązań i wykresów czasowych. Zmieniają się wartości prądów i mocy poszczególnych elementów jak również bilans mocy. Intersujące są trzy przypadki wartości reaktancji zaznaczone w programie: XL=XC (rezonans równoległy i brak przepływu prądu w rezystorze, choć prądy cewki i kondensatora są różne od zera), XL=2XC oraz XC=2XL. W ostatnich 2 przypadkach obwód zmienia swój charakter na pojemnościowy (przypadek XL=2XC) lub indukcyjny (przypadek XC=2XL). Zmiana charakteru jest uwidoczniona w postaci zmiany znaku mocy biernej wydawanej przez źródło SE.
Załączony program „Rozpływ prądów w obwodzie AC – obwód 2” przedstawia przypadek zasilania równoległego połączenia elementów R, L i C ze źródła prądowego typu sinusoidalnego o zadanej wartości skutecznej Isk, pulsacji ω i fazie początkowej φ. Pozwala obserwować wartości prądów, napięć i mocy pozornej zespolonej w poszczególnych elementach R, L, C. Użytkownik może zmieniać wartości wszystkich parametrów. Program wyświetla przebiegi czasowe napięc oraz prądów poszczególnych elementów. Warto zwrócić uwagę na fazy prądu cewki i kondensatora. Przy identycznym napięciu panującym na połączeniu równoległym tych elementów fazy tych prądów różnią się o 180o. Każda zmiana wartości jakiegokolwiek elementu powoduje automatyczną zmianę wartości rozwiązań i wykresów czasowych. Zmieniają się wartości prądów i mocy poszczególnych elementów jak również bilans mocy. Intersujące są trzy przypadki wartości reaktancji zaznaczone w programie: XL=XC (rezonans równoległy i cały prąd źródła przepływa przez rezystor, choć prądy cewki i kondensatora są różne od zera), XL=2XC oraz XC=2XL. W ostatnich 2 przypadkach obwód zmienia swój charakter na pojemnościowy (przypadek XXL=2XC) lub indukcyjny (przypadek XC=2XL). Zmiana charakteru jest uwidoczniona w postaci zmiany znaku mocy biernej wydawanej przez źródło SI.
Załączony program „Rozpływ prądów w obwodzie AC – obwód rozgałęziony” pozwala obserwować wartości prądów, napięć i mocy pozornej zespolonej w poszczególnych elementach R, L, C obwodu rozgałęzionego zasilanych z 2 źródeł: napięciowego i prądowego typu sinusoidalnego o zadanej wartości skutecznej, tej samej pulsacji ω i zadanej fazie początkowej. Użytkownik może zmieniać wartości zarówno parametrów źródła napięciowego jak i wartości poszczególnych elementów. Program wyświetla przebiegi czasowe napięcia zasilającego oraz prądów i napięć poszczególnych elementów jak również mocy chwilowej. Każda zmiana wartości jakiegokolwiek elementu powoduje automatyczną zmianę wartości rozwiązań i wykresów czasowych. Zmieniają się wartości prądów i mocy poszczególnych elementów jak również bilans mocy. Intersujące są trzy przypadki wartości reaktancji zaznaczone w programie:XL=XC (rezonans równoległy i brak przepływu prądu w rezystorze, choć prądy cewki i kondensatora są różne od zera), XL=2XC oraz XC=2XL.
3.6. Energia magazynowana w cewce i kondensatorze
Cewka i kondensator traktowane jako idealne elementy obwodowe należą do elementów magazynujących energię elektryczną i z tego punktu widzenia odgrywają ogromną rolę w elektrotechnice.
3.7. Energia magazynowana w idealnym kondensatorze
Rozpatrzmy kondensator o pojemności C zasilany ze źródła napięciowego u(t). Obliczymy energię dostarczoną do tego kondensatora w czasie od t0 do t. Energia ta może być obliczona jako całka z mocy chwilowej
| \(W(t_0,t)=\int_{t_0}^{t}{p(\tau)d\tau}\) | (3.19) |
Uwzględniając wzór na moc chwilową i dokonując odpowiednich operacji całkowania otrzymujemy
| \(W(t_0,t)=\int_{t_0}^{t}{u(\tau)i(\tau)d\tau}=\int_{t_0}^{t}{i(\tau)L\frac{di(\tau)}{d\tau}d\tau}=L\int_{i(t_0)}^{i(t)}idi\) | (3.20) |
Załóżmy, że czas t0 jest taką chwilą, w której prąd cewki i(t) jest zerowy. W takim razie wzór na energię upraszcza się do postaci
| \(W(t_0,t)=L\int_{0}^{i(t)}idi=\frac{1}{2}Li^2(t)\) | (3.21) |
Zasadniczą cechą cewki idealnej jest jej bezstratność, co oznacza, że energia dostarczona do niej pozostaje w niej zmagazynowana. Zatem cewka, przez która przepływa prąd stały I posiada energię równą
| \(W=\frac{1}{2}LI^2\) | (3.22) |
W odróżnieniu od kondensatora, w którym energia związana była z napięciem między okładkami (ładunkiem) energia cewki jest uzależniona od prądu (strumienia magnetycznego). Stąd przyjmuje się, że kondensator magazynuje energię w polu elektrycznym a cewka w polu magnetycznym.
3.8. Dopasowanie odbiornika do źródła
Rzeczywiste źródło energii elektrycznej można przedstawić w postaci szeregowego połączenia idealnego źródła napięcia E oraz impedancji wewnętrznej źródła Zg jak to przedstawiono na rys. 3.4
Rys. 3.4. Model rzeczywistego źródła napięciowego generatora
Rozważmy elementarny obwód złożony z rzeczywistego źródła napięcia oraz impedancji odbiornika Z jak to przedstawiono na rys. 3.5.
Rys. 3.5. Rzeczywiste źródło napięcia obciążone impedancją Z
Przyjmijmy ogólny model impedancji wewnętrznej źródła w postaci (znak plus przy reaktancji oznacza indukcyjność, a znak minus pojemność)
| \(Z_g=R_g\pm jX_g\) | (3.23) |
Podobnie założymy, że impedancję odbiornika stanowi połączenie szeregowe rezystancji R oraz reaktancji ±X, to jest
| \(Z=R\pm jX\) | (3.24) |
Dopasowanie odbiornika do generatora rozumiemy jako dobór takiej impedancji odbiornika, przy której odbiornik pobierze ze źródła maksymalną moc czynną. Z analizy obwodu przedstawionego na rys. 3.5 wynika, że moc czynna P odbiornika jest określona zależnością
| \(P=\left|I\right|^2R=\frac{\left|E\right|^2}{\left|Z_g+Z\right|^2}R=\frac{\left|E\right|^2R}{\left(R_g+R\right)^2+\left(\pm X_g\pm X\right)^2}\) | (3.25) |
Przy ustalonej wartości rezystancji odbiornika wyrażenie powyższe osiąga maksimum dla
| \(X=-X_g\) | (3.26) |
Znak minus oznacza, że reaktancja odbiornika powinna mieć charakter odwrotny do reaktancji generatora. Przy indukcyjnym charakterze impedancji źródła, odbiornik powinien mieć charakter pojemnościowy a przy charakterze pojemnościowym generatora odbiornik powinien mieć charakter indukcyjny.
Po uwzględnieniu tej zależności wyrażenie na moc przyjmie uproszczoną postać
| \(P=\frac{\left|E\right|^2R}{\left(R_g+R\right)^2}\) | (3.27) |
Wydzielenie maksymalnej mocy czynnej na rezystorze wymaga, aby pochodna funkcji mocy względem rezystancji R równała się zeru, czyli
| \(\frac{dP(R)}{dR}=0\) | (3.28) |
czyli
| \(\frac{\left(R_g+R\right)^2-2R\left(R_g+R\right)}{\left(R_g+R\right)^4}\left|E\right|=0\) | (3.29) |
Równane powyższe jest spełnione dla wartości rezystancji obciążenia równej rezystancji źródła, czyli
| \(R=R_g\) | (3.30) |
Można łatwo sprawdzić, że przy takim warunku druga pochodna funkcji mocy względem rezystancji jest ujemna, co oznacza, że mamy do czynienia z maksimum mocy. Ostatecznie stwierdzamy, że warunkiem dopasowania odbiornika do generatora ze względu na moc czynną jest taki dobór odbiornika, aby jego impedancja była sprzężona do impedancji generatora, to znaczy \(Z=Z_g^\ast\). Łatwo jest pokazać, że przy spełnieniu powyższego warunku na impedancji odbiornika wydzieli się maksymalna moc czynna \(P_{max}\) równa
| \({P\frac{\left|E\right|^2}{4R_g}}_{max}\) | (3.32) |
Biorąc pod uwagę, że w obwodzie istnieją dwie identyczne rezystancje (odbiornika i generatora), przez które przepływa identyczny prąd moc maksymalna odbiornika stanowi 50% całkowitej mocy wydzielanej przez źródło idealne.
4. Metody analizy złożonych obwodów RLC w stanie ustalonym przy wymuszeniu sinusoidalnym
Analiza obwodów w stanie ustalonym przy wymuszeniu sinusoidalnym tylko w najprostszym przypadku połączenia szeregowego lub równoległego elementów jest zagadnieniem prostym, nie wymagającym rozwiązywania układu równań. W obwodach zawierających małą liczbę elementów wystarczy zwykle zastosowanie równań Kirchhoffa, które w połączeniu z równaniami symbolicznymi opisującymi elementy tworzą układ równań algebraicznych o małej liczbie zmiennych. Jego rozwiązanie jest stosunkowo łatwe, a w jego wyniku otrzymuje się wszystkie prądy i napięcia w obwodzie. W przypadku obwodów złożonych zawierających bardzo dużą liczbę elementów takie podejście (aczkolwiek możliwe) jest mało efektywne, gdyż wymaga rozwiązania ogromnego układu równań o współczynnikach zespolonych. Liczba tych równań jest równa liczbie elementów obwodu .
Wykład czwarty poświęcony będzie zaawansowanym metodom analizy złożonych obwodów RLC w stanie ustalonym przy wymuszeniach sinusoidalnych. Podstawowym założeniem przy wymuszeniu sinusoidalnym jest przyjęcie opisu symbolicznego elementów obwodu, zgodnie z którym cewka opisana jest impedancją zespoloną \(Z_L=j\omega L\) a kondensator impedancją \(Z_C=-j\frac{1}{\omega C}\). Źródło sinusoidalne zastępuje się jego wartością skuteczną zespoloną, określaną według zasad podanych w wykładzie drugim.
Znanych jest wiele metod umożliwiających analizę dowolnie złożonych obwodów elektrycznych, spośród których omówimy metodę klasyczną opartą na prawach Kirchhoffa, zastosowaniu twierdzenia Thevenina i Nortona oraz metodę węzłową i oczkową. W przypadku wielu wymuszeń o różnych częstotliwościach niezbędne jest zastosowanie tak zwanej zasady superpozycji obowiązującej dla obwodów liniowych, wprowadzonej w końcowej fazie wykładu.
4.1. Metoda równań Kirchhoffa
W metodzie tej wykorzystuje się w bezpośredniej formie prawo prądowe i napięciowe Kirchhoffa uzupełnione o równania symboliczne opisujące poszczególne elementy obwodu. W efekcie zastosowania praw Kirchhoffa otrzymuje się układ równań algebraicznych o zespolonych współczynnikach. Jeśli założymy, że obwód posiada b gałęzi i n węzłów to w równaniach opisujących obwód wykorzystuje się (n-1) równań pochodzących z prawa prądowego Kirchhoffa. Pozostałe (b-n+1) równań wynika z prawa napięciowego Kirchhoffa dla (b-n+1) dowolnie wybranych oczek niezależnych w obwodzie (oczka uważa się za niezależne, jeśli równania napięciowe opisujące je są od siebie niezależne). Rozwiązanie powstałego układu równań prowadzi do wyznaczenia wartości wszystkich prądów i napięć w obwodzie.
4.2. Metoda oparta na twierdzeniu Thevenina
Jednym z ważniejszych twierdzeń w teorii obwodów jest twierdzenie Thevenina. Pozwala ono zastąpić złożony obwód elektryczny o dowolnej strukturze i wartościach elementów, przez obwód prosty będący połączeniem szeregowym jednej impedancji zastępczej oraz źródła napięciowego. Oznacza to uproszczenie obwodu do jednego oczka, co umożliwia w bardzo prosty sposób wyznaczenie prądu lub napięcia jednej wybranej gałęzi obwodu.
Twierdzenie Thevenina
Dowolny, aktywny obwód liniowy można zastąpić od strony wybranych zacisków gałęzi AB uproszczonym obwodem równoważnym, złożonym z szeregowego połączenia jednego idealnego źródła napięcia i impedancji zastępczej obwodu. Wartość źródła zastępczego oblicza się na podstawie analizy obwodu oryginalnego jako napięcie panujące na zaciskach AB. Impedancja zastępcza widziana z zacisków AB dotyczy obwodu po zwarciu wszystkich niezależnych źródeł napięcia oraz rozwarciu niezależnych źródeł prądu.
Rys. 4.1 przedstawia sposób transformacji obwodu widzianego z zacisków AB zgodnie z twierdzeniem Thevenina
Rys. 4.1 Ilustracja transformacjo obwodowej twierdzenia Thevenina
Korzystając z twierdzenia Thevenina można w prosty sposób wyznaczyć prąd w dowolnej gałęzi obwodu. Rozważmy obwód liniowy z rys. 4.2 z wyszczególnioną gałęzią AB w której poszukiwany jest prąd I. Prawa strona rysunku przedstawia otrzymany obwód po jego transformacji zgodnie z twierdzeniem Thevenina. Obwód składa się z jednego oczka którego prąd jest poszukiwanym prądem I.
Rys. 4.2. Transformacja obwodu zgodnie z twierdzeniem Thevenina
Źródło \(U_{AB}\) występujące na rysunku reprezentuje źródło zastępcze obwodu liniowego, określone jako napięcie na zaciskach AB po odłączeniu impedancji Z. Impedancja \(Z_{AB}\) jest impedancją zastępczą obwodu liniowego po odłączeniu impedancji Z i wyeliminowaniu wszystkich źródeł niezależnych (zwarciu źródeł napięciowych i rozwarciu źródeł prądowych). Poszukiwana wartość prądu płynącego przez impedancję Z może być określona przy wykorzystaniu prawa napięciowego Kirchhoffa zastosowanego do obwodu uproszczonego. Jego zastosowanie pozwala wyrazić prąd I w następującej postaci
| \(I=\frac{U_{AB}}{Z+Z_{AB}}\) | (4.1) |
Zastosowanie twierdzenia Thevenina w większości przypadków znakomicie upraszcza analizę obwodu. Jest szczególnie użyteczna w przypadkach, w których trzeba wyznaczyć tylko jeden prąd w obwodzie, gdyż można dokonać tego bez konieczności rozwiązywania układu równań algebraicznych lub przy znacznej redukcji liczby tych równań.
Korzystając z twierdzenia Thevenina wyznaczyć prąd I w gałęzi AB obwodu mostka przedstawionego na rys. 4.3, jeśli \(e(t)=10\sqrt2sin{(}\omega t)\), \(R_0=7,5\mathrm{\Omega}\), \(R_1=5\mathrm{\Omega}\), \(R_2=5\mathrm{\Omega}\) a reaktancje cewki i kondensatora są równe odpowiednio \(X_L=\omega L=5\mathrm{\Omega}\) oraz \( X_C=1/\omega C=10\mathrm{\Omega}\), \(X_{C0}=1/\omega C_0=5\mathrm{\Omega}\).
Rys. 4.3. Schemat obwodu do przykładu 4.2
Rozwiązanie
Wartości parametrów gałęzi zastępczej Thevenina oblicza się po odłączeniu gałęzi AB, w której obliczany jest prąd. Na rys. 4.4a przedstawiono schemat obwodu do wyznaczenia impedancji zastępczej Thevenina.
Rys. 4.4. Postaci obwodu do wyznaczania a) impedancji zastępczej Thevenina,
b) napięcia źródła zastępczego
Łatwo pokazać, że impedancja zastępcza tego obwodu jest równa
\(Z_{AB}=\frac{R_1R_2}{R_1+R_2}+\frac{Z_LZ_C}{Z_L+Z_C}=\frac{5\cdot5}{5+5}+\frac{j5\cdot(-j10)}{j5-j10}=2,5+j10\)
Rys. 4.4b przedstawia obwód do obliczenia wartości źródła zastępczego U_{AB} w schemacie zastępczym Thevenina. Obliczając kolejno prądy
\(I_1=\frac{E}{R_1+R_2}=1\)
\(I_2=\frac{E}{jX_L-jX_C}=2j\)
napięcie \(U_{AB}\) określa się ze wzoru
\(U_{AB}=R_1I_1-Z_CI_2=-15\)
Rys. 4.5 Schemat obwodu zastępczego wynikającego z twierdzenia Thevenina
Wykorzystując obwód zastępczy Thevenina z rys. 4.5 i prawo napięciowe Kirchhoffa, wartość skuteczną zespoloną prądu I określa się ze wzoru
\(I=\frac{U_{AB}}{Z_{AB}+R_0-jX_{C0}}=\frac{-15}{2,5+j10+7,5-j5}=\frac{-15}{11,18e^{j26}}=1,34e^{-j154^\circ}\)
Wartości chwilowe prądu i(t) określone są zależnością
\(i(t)=1,34\sqrt2sin{(}\omega t-154^\circ)A\)
Zauważmy, że zastosowanie twierdzenia Thevenina umożliwiło rozwiązanie obwodu względem jednego wybranego prądu bez konieczności rozwiązania układu równań algebraicznych opisujących cały obwód.
4.3. Metoda oparta na twierdzeniu Nortona
Twierdzenie Nortona pozwala zastąpić złożony obwód elektryczny o dowolnej strukturze i wartościach elementów, przez obwód prosty będący połączeniem równoległym jednej impedancji zastępczej oraz idealnego źródła prądowego.
Twierdzenie Nortona
Dowolny aktywny obwód liniowy można od strony wybranych zacisków AB zastąpić obwodem równoważnym, złożonym z równoległego połączenia idealnego źródła prądu i impedancji zastępczej obwodu. Wartość źródła zastępczego oblicza się w obwodzie oryginalnym jako prąd zwarciowy gałęzi AB. Impedancja zastępcza widziana z zacisków AB dotyczy obwodu po zwarciu wszystkich źródeł napięcia oraz rozwarciu źródeł prądu i jest identyczna z impedancją zastępczą w twierdzeniu Thevenina.
Rys. 4.6 przedstawia schemat transformacji obwodu zgodnie z twierdzeniem Nortona.
Rys. 4.6 Uproszczenie obwodu zgodnie z twierdzeniem Nortona
Twierdzenie Nortona, podobnie jak Thevenina pozwala obliczyć w prosty sposób prąd lub napięcie jednej wybranej gałęzi obwodu. Rozważmy obwód liniowy z rys. 4.7 z wyszczególnioną gałęzią AB w której poszukiwany jest prąd I. Po prawej stronie rysunku przedstawiono obwód po jego transformacji zgodnie z twierdzeniem Nortona.
Rys. 4.7. Schemat transformacji obwodu według twierdzenia Nortona
Prąd I oraz napięcie U występujące w gałęzi AB obwodu oryginalnego są równe odpowiednio prądowi I oraz napięciu U w tej samej gałęzi obwodu uproszczonego z prawej strony rysunku. Źródło prądowe \(I_z\) reprezentuje źródło zastępcze równe prądowi zwarciowemu na zaciskach AB, natomiast impedancja \( Z_{AB}\) jest impedancją zastępczą obwodu liniowego po wyłączeniu impedancji Z. Poszukiwane napięcie na impedancji Z oblicza się z prawa prądowego Kirchhoffa, \(I_z-U\left(\frac{1}{Z}+\frac{1}{Z_{AB}}\right)=0\), które pozwala wyrazić napięcie U gałęzi w postaci
| \(U=\frac{I_z}{1/Z+1/Z_{AB}}\) | (4.2) |
Znajomość napięcia U pozwala wyznaczyć na podstawie prawa Ohma prąd gałęzi korzystając z zależności \(I=U/Z\). Podobnie jak metoda Thevenina, zastosowanie twierdzenia Nortona umożliwia obliczenie prądu i napięcia tylko jednej wyszczególnionej gałęzi obwodu. Zwykle z punktu widzenia obliczeniowego wygodniejsze jest użycie metody Thevenina.
4.4. Równoważność twierdzenia Thevenina i Nortona
Twierdzenia Thevenina i Nortona pozwalają wyznaczyć uproszczone schematy zastępcze tego samego układu elektrycznego z punktów AB obwodu oryginalnego. Oba schematy uproszczone stanowią więc obwody zastępcze równoważne sobie, co oznacza, że prąd i napięcie w gałęzi AB, która nie uległa zmianie w wyniku transformacji w obu obwodach są takie same. Oznacza to, że gałąź szeregowa zawierająca idealne źródło napięcia E i impedancję Z może być bez zmiany prądu w obwodzie zewnętrznym zastąpiona gałęzią równoległą zawierającą idealne źródło prądowe I oraz impedancję Z, jak to zilustrowano na rys. 4.8.
Rys. 4.8. Równoważność obwodów zastępczych Thevenina i Nortona
Dla uzyskania jednakowych wartości napięcia U wzajemne relacje między wartościami źródła prądu i napięcia określa wzór
| \(I=\frac{E}{Z}\) | (4.3) |
przy zamianie gałęzi szeregowej na równoległą oraz
| \(E=ZI\) | (4.4) |
przy zamianie gałęzi równoległej na szeregową. Impedancja Z w obu obwodach zastępczych pozostaje taka sama.
4.5. Metoda potencjałów węzłowych
Metoda potencjałów węzłowych, zwana również metodą węzłową, jest jedną z najogólniejszych i najczęściej stosowanych metod, pozwalających wyznaczyć prądy wszystkich gałęzi występujących w obwodzie. Jako zmienne przyjmuje się w niej potencjały poszczególnych węzłów obwodu określane względem jednego arbitralnie wybranego węzła uznanego za węzeł odniesienia („masy”), którego potencjał przyjmuje się za równy zeru. Liczba równań w tej metodzie jest równa liczbie węzłów niezależnych a więc znacznie mniejsza niż w metodzie wykorzystującej bezpośrednio układ równań otrzymanych w wyniku zastosowania praw Kirchhoffa.
Metoda węzłowa wynika bezpośrednio z równań prądowych Kirchhoffa napisanych dla wszystkich węzłów niezależnych w obwodzie. Prąd każdej gałęzi obwodu jest wyrażany za pośrednictwem potencjałów węzłowych, czyli napięć węzłów mierzonych względem węzła odniesienia. Zostało wykazane, że każdy obwód liniowy RLC może być opisany równaniem macierzowym potencjałów węzłowych o postaci
| \(YV={I}_{zr}\) | (4.5) |
Rozwiązanie tego równania może być zapisane przy użyciu inwersji macierzy Y w postaci
| \({V}={Y}^{-1}{I}_{zr}\) | (4.6) |
Przy założeniu, że obwód ma N węzłów niezależnych macierz Y jest macierzą o wymiarach N\times N. Wektor V jest zbiorem niezależnych potencjałów węzłowych o wymiarze N a \mathbit{I}_{zr} jest wektorem prądów źródłowych stanowiących wymuszenie. Macierz węzłowa Y określona jest w postaci
| \({Y}=\left[\begin{matrix}Y_{11}&Y_{12}&...&Y_{1N}\\Y_{21}&Y_{22}&...&Y_{2N}\\...&...&...&...\\Y_{N1}&Y_{N2}&...&Y_{NN}\\\end{matrix}.\right]\) | (4.6) |
a wektory V oraz \mathbit Izr dane są jak następuje
| \({V}=\left[\begin{matrix}V_1\\V_2\\...\\V_N\\\end{matrix}\right]\) | (4.7) |
| \({I}_{zr}=\left[\begin{matrix}I_{zr1}\\I_{zr2}\\...\\I_{zrN}\\\end{matrix}\right]\) | (4.8) |
Elementy \(Y_{ii}\) położone na głównej diagonalnej macierzy Y nazywane są admitancjami własnymi węzła i-tego. W przypadku obwodów RLC bez źródeł sterowanych admitancja własna węzła i-tego jest równa sumie admitancji wszystkich gałęzi włączonych w i-tym węźle. Elementy \(Y_{ij}\) położone poza główną diagonalną są admitancjami wzajemnymi między węzłem i-tym oraz j-tym. Admitancja wzajemna dwu węzłów jest równa admitancji łączącej te węzły wziętej ze znakiem minus. Admitancja wzajemna węzła i-tego oraz j-tego jest taka sama jak węzła j-tego oraz i-tego, tzn. \(Y_{ij}=Y_{ji}\). Macierz admitancyjna Y dla obwodów RLC bez źródeł sterowanych jest więc macierzą symetryczną.
Elementy wektora wymuszeń prądowych \({I}_{zr}\) są równe sumie wszystkich prądów źródłowych wpływających do danego węzła, przy czym prąd źródłowy dopływający do węzła bierze się ze znakiem plus a prąd odpływający od węzła ze znakiem minus.
Podsumowując, analiza obwodów w stanie ustalonym metoda węzłową wymaga wykonania następujących etapów:
- Opis obwodu równaniem macierzowym potencjałów węzłowych (zmienne poszukiwane: wektor potencjałów \(V\))
- Rozwiązanie układu równań \({YV}={I}_{zr}\)
- Określenie prądów gałęziowych z prawa napięciowego Kirchhoffa przy znanych potencjałach węzłowych: prąd gałęziowy jest równy iloczynowi admitancji elementu i napięcia na nim wyrażonego poprzez znane potencjały węzłowe.
- Należy podkreślić, że metoda potencjałów węzłowych dopuszcza istnienie w obwodzie jedynie źródeł wymuszających typu prądowego. Jeśli w obwodzie występują również źródła napięciowe należy je przekształcić w odpowiednie źródła prądowe wykorzystując do tego celu równoważność Thevenina – Nortona (patrz rys. 4.8).
Sposób formułowania równań węzłowych zilustrujemy na przykładzie obwodu przedstawionego na rys. 4.9.
Korzystając z przedstawionych reguł formułowania równań węzłowych należy napisać równanie potencjałów węzłowych dla obwodu przedstawionego na rys. 4.9.
Rys. 4.9 Schemat obwodu do przykładu 4.2
Rozwiązanie
Obwód zawiera 3 węzły niezależne o potencjałach: \(V_1\), \(V_2\) oraz \(V_3\) mierzonych względem węzła odniesienia jak to oznaczono na rysunku. Oznaczając admitancje przez Y, gdzie Y=1/Z otrzymuje się opis węzłowy \({YV}={I}_{zr}\) obwodu
\(\left[\begin{matrix}Y_2&-Y_2&0\\-Y_2&Y_2+Y_3+Y_4&-Y_4\\0&-Y_4&Y_4+Y_5+Y_6\\\end{matrix}\right]\left[\begin{matrix}V_1\\V_2\\V_3\\\end{matrix}\right]=\left[\begin{matrix}I_{z1}+I_{z2}\\E_3Y_3-I_{z2}-I_{z4}\\I_{z4}-I_{z6}-E_5Y_5\\\end{matrix}\right]\)
w którym macierz potencjałów węzłowych Y oraz wektor prądów wymuszających \({I}_{zr}\) określone są w postaci
\({Y}=\left[\begin{matrix}Y_2&-Y_2&0\\-Y_2&Y_2+Y_3+Y_4&-Y_4\\0&-Y_4&Y_4+Y_5+Y_6\\\end{matrix}\right]\)
\({I}_{zr}=\left[\begin{matrix}I_{z1}+I_{z2}\\E_3Y_3-I_{z2}-I_{z4}\\I_{z4}-I_{z6}-E_5Y_5\\\end{matrix}\right]\)
Na podstawie obliczonych wartości napięć węzłowych obwodu można w prosty sposób korzystając z prawa napięciowego Kirchhoffa dla poszczególnych gałęzi obwodu wyznaczyć prądy gałęziowe. Wystarczy w tym celu zastosować bądź prawo Ohma (jeśli gałąź zawiera jedynie element pasywny) lub równanie napięciowe Kirchoffa dla gałęzi szeregowej zawierającej źródło napięcia i element pasywny. Przykładowo dla obwodu z rys. 4.7 odpowiednie zależności przyjmują postać
\(I_2=Y_2(V_1-V_2)\)
\(I_3=Y_3(V_2-E_3)\)
\(I_4=Y_4(V_2-V_3)\)
\(I_5=Y_5(V_3+E_5)\)
\(I_6=Y_6V_3\)
Należy podkreślić, że metoda potencjałów węzłowych wymaga rozwiązania układu N równań, gdzie N oznacza liczbę węzłów niezależnych. Zwykle liczba węzłów jest dużo mniejsza niż liczba gałęzi obwodu, stąd metoda potencjałów węzłowych jest znacznie prostsza niż metoda klasyczna wykorzystująca bezpośrednio prawa Kirchhoffa dla całego obwodu.
Reguły tworzenia opisu węzłowego przedstawione powyżej zakładały istnienie jedynie elementów pasywnych RLC oraz źródeł wymuszających typu prądowego. Przy takim założeniu są one bardzo proste i łatwe w stosowaniu. W przypadku wystąpienia źródeł sterowanych w obwodzie trudno jest podać jednoznaczną formułę ogólną pozwalającą określić bezpośrednio zarówno macierz admitancyjną jak i wektor wymuszeń prądowych. Tworząc opis admitancyjny w takim przypadku można w pierwszym kroku zaliczyć źródła sterowane do źródeł wymuszających i tworzyć opis admitancyjny identycznie jak dla obwodu pasywnego. W drugim kroku wszystkie źródła sterowane należy wyrazić poprzez potencjały węzłowe przerzucając elementy wymuszeń uzależnione od tych potencjałów na lewą stronę równań (do macierzy węzłowej). Macierz admitancyjna Y wynika z uporządkowania powstałego macierzowego układu równań. W efekcie powstaje standardowy opis admitancyjny obwodu, który nie musi już teraz spełniać warunku symetrii macierzy Y.
Należy zwrócić uwagę na uproszczenia wynikające z istnienia w obwodzie idealnego źródła napięcia. Źródło takie ustala potencjał określonego węzła (gdy jest włączone względem węzła odniesienia) lub uzależnia potencjał jednego węzła względem drugiego (gdy jest włączone między dwoma węzłami niezależnymi). W obu przypadkach prowadzi to do redukcji liczby równań opisujących obwód.
4.6. Metoda prądów oczkowych
W metodzie prądów oczkowych, zwanej również metodą oczkową, wprowadza się prądy oczkowe jako zmienne, czyli prądy przypisane niezależnym oczkom występującym w obwodzie. Przykładowy wybór oczek niezależnych i oznaczenie prądów oczkowych obwodu przedstawiono na rys. 4.10 (należy zaznaczyć, że jest to jeden z możliwych wyborów oczek).
Rys. 4.10. Przykład wyboru oczek niezależnych w obwodzie
Oznaczmy w ogólności wektor prądów oczkowych w postaci
| \({I}_o=\left[\begin{matrix}I_{o1}\\I_{o2}\\...\\I_{oN}\\\end{matrix}\right]\) | (4.9) |
w której \(I_{ok}\) oznacza prąd oczkowy k-tego oczka. Dla uzyskania opisu oczkowego wykorzystuje się prawo napięciowe Kirchhoffa napisane dla wszystkich oczek niezależnych obwodu. Następnie wyraża się wszystkie prądy gałęziowe poprzez prądy oczkowe (prąd gałęziowy jest równy sumie lub różnicy prądów oczkowych przeprowadzonych przez daną gałąź) i otrzymuje opis obwodu w postaci macierzowego układu równań oczkowych
| \({Z}{I}_o={E}\) | (4.10) |
gdzie macierz oczkowa Z oraz wektor napięć wymuszających E przyjmują postać
| \({Z}=\left[\begin{matrix}Z_{11}&Z_{12}&...&Z_{1N}\\Z_{21}&Z_{22}&...&Z_{2N}\\...&...&...&...\\Z_{N1}&Z_{N2}&...&Z_{NN}\\\end{matrix}.\right]\) | (4.11) |
| \({E}=\left[\begin{matrix}E_{o1}\\E_{o2}\\...\\E_{oN}\\\end{matrix}\right]\) | (4.12) |
Elementy Z_{ii} położone na głównej diagonalnej macierzy Z nazywamy impedancjami własnymi oczka i-tego. Przy założeniu, że wszystkie prądy oczkowe mają identyczny zwrot, dla obwodów RLC bez źródeł sterowanych impedancja własna oczka i-tego jest równa sumie impedancji wszystkich gałęzi występujących w oczku. Elementy \(Z_{ij}\) położone poza główną diagonalną są impedancjami wzajemnymi między oczkiem i-tym oraz j-tym. Impedancja wzajemna dwu oczek przy identycznym zwrocie wszystkich prądów oczkowych jest równa impedancji wspólnej dla obu oczek wziętej ze znakiem minus. Impedancja wzajemna oczka i-tego oraz j-tego jest taka sama jak oczka j-tego oraz i-tego, tzn. \(Z_{ij}=Z_{ji}\).
Macierz Z jest więc macierzą symetryczną.
Element k-ty wektora wymuszeń napięciowych E jest równy sumie wszystkich napięć źródłowych występujących w k-tym oczku. Przy założonej orientacji oczka napięcie źródłowe dodaje się ze znakiem plus jeśli jego zwrot jest identyczny z tą orientacją a ze znakiem minus jeśli ten zwrot jest przeciwny. Sposób tworzenia opisu oczkowego zilustrujemy na przykładzie obwodu z rys. 4.11.
Przy wystąpieniu źródeł sterowanych, podobnie jak w opisie węzłowym, nie istnieje bezpośrednia formuła pozwalająca na automatyczny opis macierzowy obwodu. W takim przypadku tworząc opis macierzą oczkową należy w pierwszym kroku zaliczyć źródła sterowane do źródeł wymuszających i stworzyć opis oczkowy identycznie jak dla obwodu pasywnego. W drugim kroku wszystkie źródła sterowane należy wyrazić poprzez prądy oczkowe przerzucając elementy wymuszeń uzależnione od tych prądów na lewą stronę równań (do macierzy oczkowej). Macierz impedancyjna Z wynika z uporządkowania powstałego macierzowego układu równań.
Dla obwodu przedstawionego na rys. 4.11 napisać równanie prądów oczkowych przy założeniu układu oczek niezależnych jak na rysunku.
Rys. 4.11 Schemat obwodu do przykładu 4.3
Rozwiązanie
Obwód zawiera 3 oczka niezależne, stąd wymiar macierzy oczkowej jest równy 3, podobnie jak liczba nieznanych składników wektora prądów oczkowych oraz liczba znanych składników wektora napięć wymuszających. Korzystając z podanej wcześniej reguły tworzenia opisu oczkowego otrzymuje się
\({Z}=\left[\begin{matrix}Z_1+Z_2+Z_3&-Z_3&-Z_1\\-Z_3&Z_3+Z_4+Z_5&-Z_5\\-Z_1&-Z_5&Z_1+Z_5+Z_6\\\end{matrix}\right]\)
\({E}=\left[\begin{matrix}-E_1-E_3\\E_3+E_4\\E_1-E_6\\\end{matrix}\right]\)
Biorąc pod uwagę że obwód zawiera trzy nieznane prądy oczkowe tworzące wektor prądów \({I}_o={\left[\begin{matrix}I_{o1}&I_{o2}&I_{o3}\\\end{matrix}\right]}^T\), równanie oczkowe \({Z}{I}_o={E}\) stanowi zbiór trzech równań liniowych. Rozwiązanie tego układu równań pozwala określić te zmienne, a w konsekwencji również. wszystkie prądy gałęziowe obwodu. Mianowicie
\(I_1=I_{o3}-I_{o1}\)
\(I_2=I_{o1}\)
\(I_3=I_{o1}-I_{o2}\)
\(I_4=I_{o2}\)
\(I_5=I_{o3}-I_{o2}\)
\(I_6=-I_{o3}\)
Metoda prądów oczkowych wymaga rozwiązania układu N równań, gdzie N oznacza liczbę oczek niezależnych. Podobnie jak w metodzie węzłowej liczba oczek jest zwykle dużo mniejsza niż liczba gałęzi obwodu, stąd metoda prądów oczkowych jest dużo bardziej efektywna niż metoda klasyczna wykorzystująca bezpośrednio prawa Kirchhoffa.
4.7. Zasada superpozycji
Omówione wcześniej metody analizy symbolicznej stanowią dobry i skuteczny sposób rozwiązania problemu przy istnieniu w obwodzie źródeł sinusoidalnych o tej samej częstotliwości, gdyż dla każdego źródła elementy reaktancyjne LC przedstawiają sobą te same wartości reaktancji. Istotna trudność występuje dopiero przy istnieniu w obwodzie wielu źródeł o różnych częstotliwościach. W takim przypadku nie istnieje pojęcie impedancji wspólnej dla każdego źródła, co uniemożliwia zastosowanie metody symbolicznej. Jedynym rozwiązaniem pozostaje wtedy zastosowanie zasady superpozycji. Obowiązuje ona tylko dla obwodów liniowych. Jej treść jest następująca.
Zasada superpozycji
Odpowiedź czasowa obwodu elektrycznego liniowego o wielu wymuszeniach przy warunkach początkowych zerowych jest równa sumie odpowiedzi czasowych na każde wymuszenie z osobna.
Tak ogólnie sformułowana zasada obowiązuje zarówno w stanie ustalonym jak i nieustalonym obwodu. W przypadku analizy stanów ustalonych jej zastosowanie w analizie obwodów polega na rozbiciu danego obwodu o wielu wymuszeniach na wiele obwodów zawierających jedynie wymuszenia o tej samej częstotliwosci, rozwiązaniu każdego z nich oddzielnie a następnie zsumowaniu odpowiedzi czasowych każdego obwodu. Należy pamiętać przy tym o zasadzie, że eliminowane źródła są zastępowane zwarciem (jeśli źródło jest napięciowe) lub rozwarciem (gdy źródło jest prądowe).
Ilustrację sposobu stosowania zasady superpozycji w analizie obwodów liniowych przedstawiono na rys. 4.12.
Rys. 4.12. Ilustracja zasady superpozycji w obwodach liniowych
Należy podkreślić, że zgodnie z zasadą superpozycji sumowanie odpowiedzi pochodzących od różnych wymuszeń może odbywać się wyłącznie w dziedzinie czasu. Sumowanie wartości zespolonych od poszczególnych wymuszeń byłoby poważnym błędem, gdyż sugerowałoby istnienie rozwiązania obwodu zawierającego tylko jedną harmoniczną o niekreślonej częstotliwości.
Zasada superpozycji odgrywa podstawową rolę przy analizie obwodów zawierających źródła sinusoidalne o różnych częstotliwościach. W takim przypadku należy zastosować analizę obwodu tyle razy, ile różnych częstotliwości występuje w obwodzie. Źródła o tej samej częstotliwości są grupowane i poddawane pojedynczej analizie.