Podręcznik
1. Sieci radialne RBF
1.3. Metody uczenia sieci neuronowych radialnych
Wprowadzone w poprzednim podrozdziale metody doboru wag \( w_i \) warstwy wyjściowej sieci radialnej RBF opierały się na założeniu, że parametry samych funkcji bazowych są znane, w związku z czym macierze Greena są określone w sposób numeryczny i zadanie sprowadza się do rozwiązania nadmiarowego układu równań liniowych o postaci (4.7). W rzeczywistych zastosowaniach liczba neuronów ukrytych \( K < p \) i problem uczenia sieci RBF z uwzględnieniem wybranego typu radialnej funkcji bazowej sprowadza się do:
-
ustalenia liczby neuronów gaussowskich \( K \) oraz doboru centrów \( \mathbf{c}_i \) i parametrów szerokości \( \mathbf{\sigma}_i \) funkcji bazowych Gaussa
-
doboru wag \( w_i \) neuronów warstwy wyjściowej.
4.3.1 Proces samoorganizacji w określeniu parametrów funkcji radialnych
Określenie wartości parametrów funkcji radialnych (centra \( \mathbf{c}_i \) i szerokości \( \mathbf{<span>\sigma}_i \)) można uzyskać przy zastosowaniu algorytmu samoorganizacji poprzez współzawodnictwo. Proces samoorganizacji danych uczących poprzez współzawodnictwo dzieli automatycznie przestrzeń na tak zwane wieloboki Voronoia, przedstawiające obszary dominacji określonych centrów odpowiadających poszczególnym funkcjom radialnym. Przykład takiego podziału przestrzeni dwuwymiarowej pokazano na rys. 4.2.
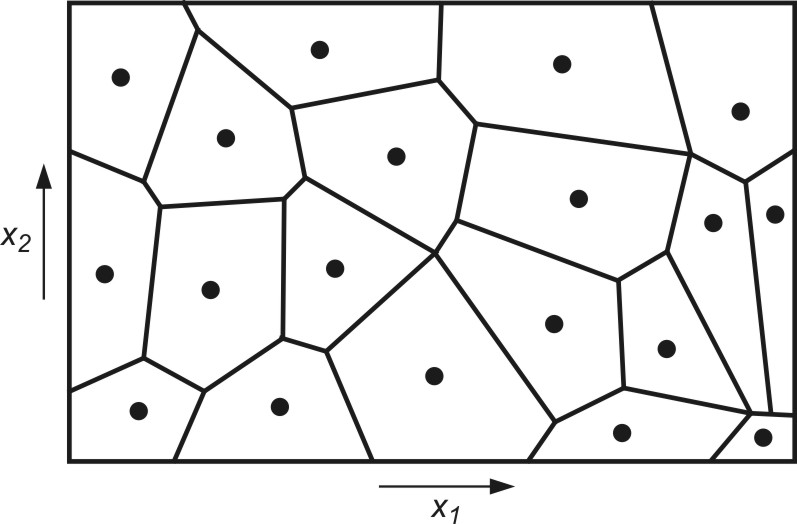
Dane zgrupowane wewnątrz klastra są reprezentowane przez punkt centralny, stanowiący średnią ze wszystkich elementów danego klastra. Centrum klastra utożsamione będzie dalej z centrum c odpowiedniej funkcji radialnej. Liczba tych funkcji jest zatem równa liczbie centrów i może być korygowana przez algorytm samoorganizacji.
Proces podziału danych na klastry można przeprowadzić przy użyciu jednej z wersji algorytmu Linde-Buzo-Graya (LBG) zwanego również algorytmem K-uśrednień (ang. K-means). W wersji bezpośredniej (on-line) tego algorytmu aktualizacja centrów następuje po każdej prezentacji wektora \( \mathbf{x} \) ze zbioru danych uczących. W wersji skumulowanej (off-line) centra są aktualizowane jednocześnie po zaprezentowaniu wszystkich składników zbioru uczącego. W obu przypadkach wstępny wybór centrów odbywa się najczęściej losowo przy wykorzystaniu rozkładu równomiernego w zakresie zmienności poszczególnych składowych wektora \( \mathbf{x} \).
W wersji bezpośredniej (on-line) po zaprezentowaniu \( k \)-tego wektora \( \mathbf{x}_k \) ze zbioru uczącego selekcjonowane jest centrum \( \mathbf{c}_i \) najbliższe w sensie wybranej metryki danemu wektorowi. To centrum podlega aktualizacji zgodnie z algorytmem WTA
| \( \mathbf{c}_i(k+1)=\mathbf{c}_i(k)+\eta\left(\mathbf{x}_k-\mathbf{c}_i(k)\right) \) | (4.9) |
w którym \( \eta \) jest współczynnikiem uczenia o małej wartości (zwykle \( \eta \ll 1 \)), malejącym w czasie do zera. Pozostałe centra nie ulegają zmianie. Każdy wektor uczący \( \mathbf{x} \) jest prezentowany wielokrotnie, zwykle w kolejności losowej aż do ustalenia wartości centrów.
Stosowana jest również odmiana algorytmu, w której centrum zwycięskie adaptowane jest według wzoru (4.9), a jeden lub kilka najbliższych mu centrów odpychane w przeciwnym kierunku, przy czym realizacja procesu odpychania odbywa się zgodnie ze wzorem
| \( \mathbf{c}_i(k+1)=\mathbf{c}_i(k)-\eta_1\left(\mathbf{x}_k-\mathbf{c}_i(k)\right) \) | (4.10) |
Taka modyfikacja algorytmu pozwala na rozsunięcie centrów położonych blisko siebie i lepszą penetrację przestrzeni danych (zwykle \( \eta_1 \) < \(\eta \)).
W wersji skumulowanej uczenia prezentowane są wszystkie wektory uczące \( \mathbf{x} \) i każdy z nich przyporządkowany odpowiedniemu centrum. Zbiór wektorów przypisanych do jednego centrum tworzy klaster, którego nowe centrum jest średnią poszczególnych wektorów składowych
| \( \mathbf{c}_i(k+1)=\frac{1}{N_i} \sum_{j=1}^{N_i} \mathbf{x}_j \) | (4.11) |
gdzie \( N_i \) oznacza liczbę wektorów \( \mathbf{x}_j \) przypisanych w \( k \)-tym cyklu do \( i \)-tego centrum. Uaktualnianie wartości wszystkich centrów odbywa się równolegle. Proces prezentacji zbioru wektorów \( \mathbf{x} \) oraz uaktualniania wartości centrów powtarzany jest wielokrotnie aż do ustalenia się wartości centrów.
W praktyce używa się najczęściej algorytmu bezpośredniego ze względu na jego nieco lepszą zbieżność. Oba algorytmy nie gwarantują jednak bezwzględnej zbieżności do rozwiązania optymalnego w sensie globalnym, a jedynie zapewniają optymalność lokalną, uzależnioną od warunków początkowych i parametrów procesu. Przy niefortunnie dobranych warunkach początkowych pewne centra mogą utknąć w regionie, w którym liczba danych uczących jest znikoma lub żadna i proces modyfikacji ich położeń może zostać zahamowany. Pewnym rozwiązaniem tego problemu jest modyfikacja położeń wielu centrów na raz, ze stopniowaniem wartości stałej uczenia \( \eta \) dla każdego z nich. Centrum najbliższe aktualnemu wektorowi \( \mathbf{x} \) modyfikowane jest najbardziej, pozostałe w zależności od ich odległości względem wektora \( \mathbf{x} \) coraz mniej.
Po ustaleniu położeń centrów dobierane są wartości parametrów \( \sigma \), odpowiadających poszczególnym funkcjom bazowym. Parametr \( \sigma_j \) funkcji radialnej decyduje o kształcie funkcji i wielkości pola recepcyjnego, dla którego wartość tej funkcji jest niezerowa (większa od pewnej ustalonej wartości progowej). Dobór \( \sigma_j \) powinien być taki, aby pola recepcyjne wszystkich funkcji radialnych pokrywały cały obszar danych wejściowych, przy czym sąsiednie pola recepcyjne mogą pokrywać się w stopniu nieznacznym. Przy takim doborze wartości \( \sigma_j \) odwzorowanie funkcji realizowane przez sieci radialne będzie stosunkowo gładkie. W najprostszym rozwiązaniu za wartość \( \sigma_j \) odpowiadającą \( j \)-tej funkcji radialnej przyjmuje się odległość euklidesową \( j \)-tego centrum \( \mathbf{c}_j \) od jego najbliższego sąsiada [24,46]. W innym algorytmie z uwzględnieniem szerszego sąsiedztwa, na wartość \( \sigma_j \) wpływa odległość \( j \)-tego centrum od jego \( q \) najbliższych sąsiadów. Wartość \( \sigma_j \) określa się wtedy ze wzoru
| \( \sigma_j=\sqrt{\frac{1}{q} \sum_{k=1}^q\left\|\mathbf{c}_j-\mathbf{c}_k\right\|^2} \) | (4.12) |
W praktyce wartość \( q \) mieści się zwykle w zakresie od 3 do 6. W przypadku danych o podobnym charakterze zmian stosuje się często stałą wartość \( \sigma_j = \sigma\) dla wszystkich neuronów radialnych (dla danych znormalizowanych typowe wartości jest \( \sigma\) bliskie jedności).
Wstępny dobór liczby funkcji radialnych (neuronów ukrytych) dla każdego problemu jest sprawą kluczową, decydującą o dokładności odwzorowania. Stosuje się ogólną zasadę, że im większy jest wymiar wektora \( \mathbf{x} \) i liczba danych uczących, tym większa wymagana liczba funkcji radialnych. Często przyjmuje się na wstępie liczbę funkcji radialnych jako pewien ułamek (np. 1/3) liczby wszystkich par uczących \( p \).
4.3.2 Dobór wartości wag warstwy wyjściowej
Prosty jest również problem adaptacji wag neuronów warstwy wyjściowej. Zgodnie z zależnością (4.8) wektor wagowy \( \mathbf{x} \) może być wyznaczony w jednym kroku przez pseudoinwersję macierzy \( \mathbf{G} \), czyli \( \mathbf{W}=\left[\begin{array}{ll} \mathbf{1} & \mathbf{G} \end{array}\right]^{+} \cdot \mathbf{d} \). Dla uproszczenia wzorów przyjęto w dalszych rozważaniach oznaczenie rozszerzonej macierzy Greena \( \mathbf{G} \leftarrow [ \mathbf{1} \; \mathbf{G} ] \). W praktyce obliczenie pseudoinwersji macierzy \( \mathbf{G} \) następuje przy zastosowaniu dekompozycji według wartości osobliwych (SVD), według którego
| \( \mathbf{G} = \mathbf{USV}^T \) | (4.13) |
Macierze \( \mathbf{U} \) i \( \mathbf{V} \) są ortogonalne, o wymiarach odpowiednio \( p \times p \) oraz \( K \times K \), podczas gdy \( \mathbf{S} \) jest macierzą pseudodiagonalną o wymiarach \( p \times K \; (p < K) \), zawierającą elementy diagonalne zwane wartościami osobliwymi \( s_1 \geq s_2 \geq \ldots s_K \geq 0 \). Załóżmy, że jedynie \( r \) pierwszych elementów \( s_i \) ma znaczące wartości, a pozostałe są pomijalnie małe. Wtedy można zredukować liczbę kolumn macierzy ortogonalnych \( \mathbf{U} \) i \( \mathbf{V} \) do wartości \( r \), pomijając pozostałe. Utworzone w ten sposób zredukowane macierze \( \mathbf{U}_r \) i \( \mathbf{V}_r \) mają postać
\( \mathbf{U}_r=\left[\mathbf{u}_1, \mathbf{u}_2, \ldots, \mathbf{u}_r\right] \)
\( \mathbf{V}_r=\left[\mathbf{v}_1, \mathbf{v}_2, \ldots, \mathbf{v}_r\right] \)
a macierz \( \mathbf{S}_{r}=\operatorname{diag}\left[{s}_1, {s}_2, \ldots, {s}_{r}\right] \) staje się macierzą w pełni diagonalną (kwadratową). Macierze te aproksymują zależność (4.13) w postaci
| \( \mathbf{G} = \mathbf{U}_r \mathbf{S}_r \mathbf{V}_r^T \) | (4.14) |
Biorąc pod uwagę własności macierzy ortogonalnych (\( \mathbf{Q}^{-1} = \mathbf{Q}^{T} \)) macierz pseudoodwrotna do \( \mathbf{G} \) określona jest teraz prostą zależnością
| \( \mathbf{G}^{+} = \mathbf{V}_r \mathbf{S}_r^{-1} \mathbf{U}_r^T \) | (4.15) |
w której \( \mathbf{S}_r^{-1}=\left[ \frac{1}{s_1}, \frac{1}{s_2}, \ldots, \frac{1}{s_r} \right] \) a wektor wag sieci podlegającej adaptacji określony jest wzorem
| \( \mathbf{w} = \mathbf{V}_r \mathbf{S}_r^{-1} \mathbf{U}_r^T \mathbf{d}\) | (4.16) |
Zaletą takiego podejścia jest dobre uwarunkowanie problemu. Dobór wag wyjściowych sieci odbywa się w jednym kroku przy wykorzystaniu jedynie mnożenia odpowiednich macierzy, przy czym część macierzy (\( \mathbf{U}_r \) i \( \mathbf{V}_r \)) to macierze ortogonalne, z natury dobrze uwarunkowane (współczynnik uwarunkowania równy 1).
Zauważmy, że w uczeniu sieci RBF parametry podlegające adaptacji tworzą dwie niezależnie dobierane grupy: parametry funkcji radialnych adaptowane poprzez grupowanie danych oraz wagi \( \mathbf{w} \) warstwy wyjściowej określane poprzez pseudoinwersję macierzy Greena. Daje to efekt uproszczenia obliczeń i znacznego skrócenia czasu uczenia.
