Podręcznik: Przykład zastosowania sieci radialnej w aproksymacji

1. Sieci radialne RBF

1.6. Przykład zastosowania sieci radialnej w aproksymacji

Sieci neuronowe o radialnych funkcjach bazowych znajdują zastosowanie zarówno w rozwiązywaniu problemów klasyfikacyjnych (na wyjściu sieci umieszcza się wówczas dodatkowo funkcję typu signum, wskazująca na określona klasę), zadaniach aproksymacji funkcji wielu zmiennych jak i zagadnieniach predykcji, a więc w tym obszarze zastosowań, gdzie sieci sigmoidalne mają od lat ugruntowaną pozycję. Sieci RBF wykonują te same zadania co sieci sigmoidalne choć w rozwiązaniu problemu stosują inny sposób przetwarzania danych, wykorzystujący lokalność odwzorowania. Dzięki tej własności możliwe jest znaczne uproszczenie, a przez to również skrócenie procesu uczenia. Jako przykład zastosowania sieci RBF rozpatrzymy problem aproksymacji funkcji nieliniowej dwu zmiennych opisanej wzorem

$f(\mathbf{x})=\frac{\sin \left(\sqrt{x_1^2+x_2^2}\right)}{\sqrt{x_1^2+x_2^2}}$

(4.30)

Dla wytrenowania sieci RBF należy w pierwszej kolejności utworzyć na podstawie tego wzoru zbiór par uczących $( \mathbf{x}, d(\mathbf{x}))$ . Dane uczące utworzono dla 400 punktów danych, wygenerowanych dla zmiennych $x_1$ i $x_2$ rozłożonych równomiernie w zakresie (-9, 9). Dane te tworzą kształt funkcji trójwymiarowej przedstawionej na rys. 4.5a. Rys. 4.5b ilustruje położenia centrów funkcji bazowych wyselekcjonowanych przez sieć neuronową a rys. 4.5c i d odpowiednio postać funkcji odtworzonej oraz błąd odwzorowania. Szerokość funkcji radialnych była dobierana automatycznie w uzależnieniu od trzech najbliższych sąsiadów.

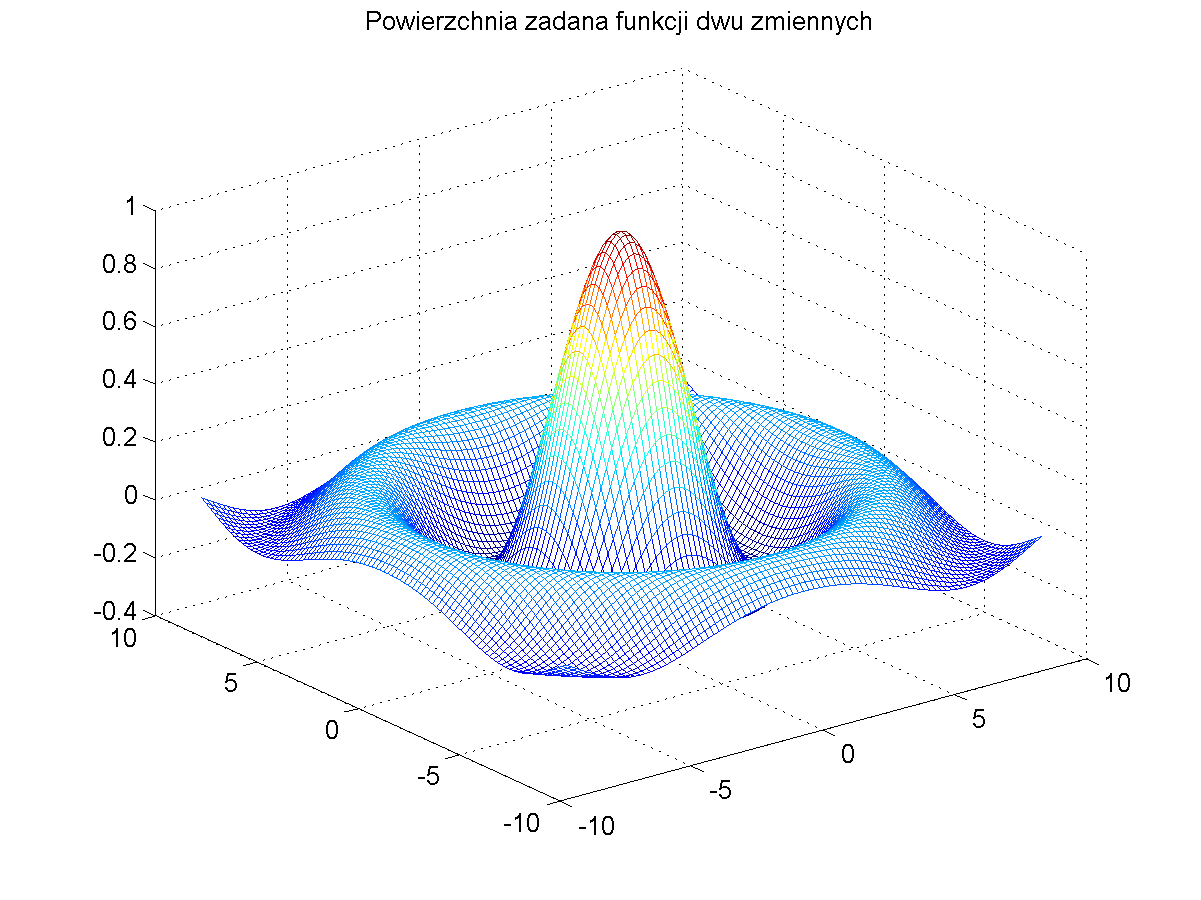
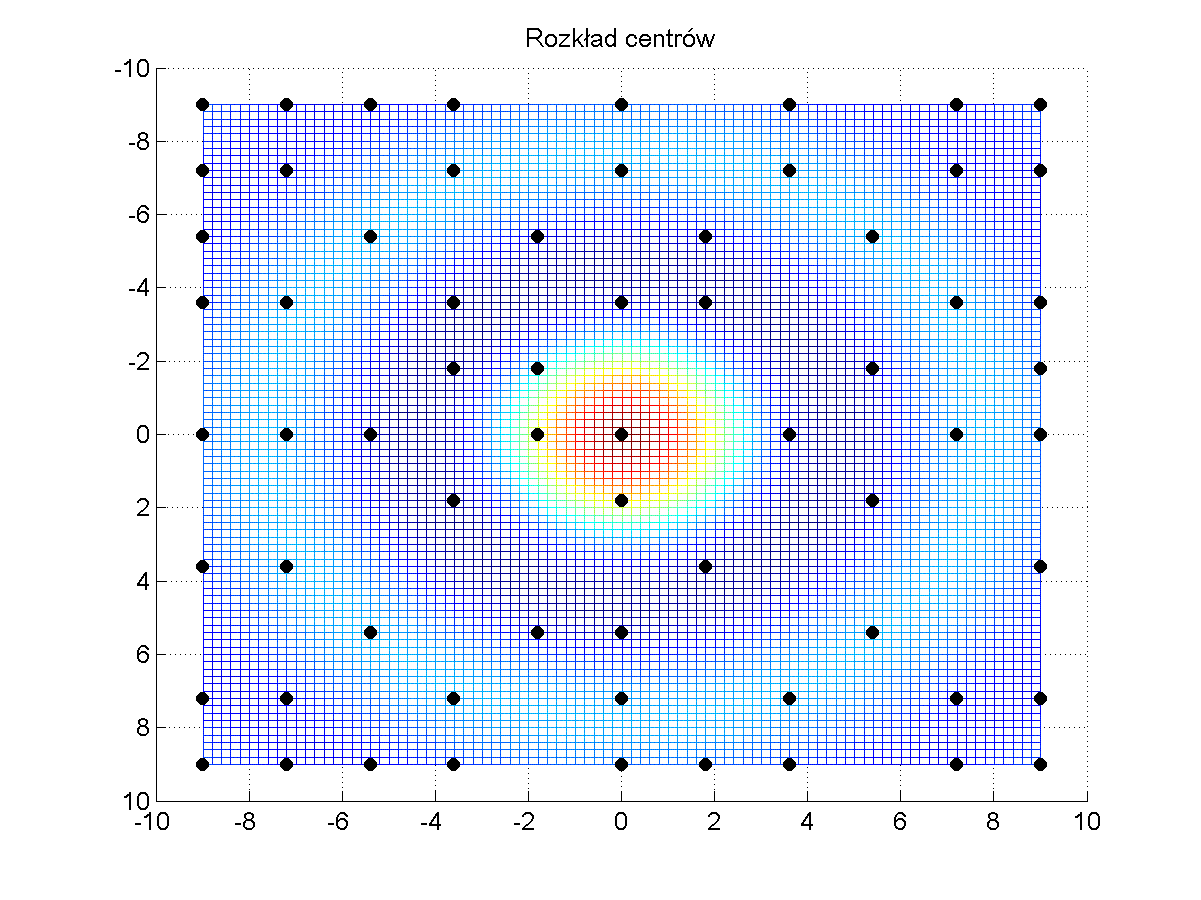
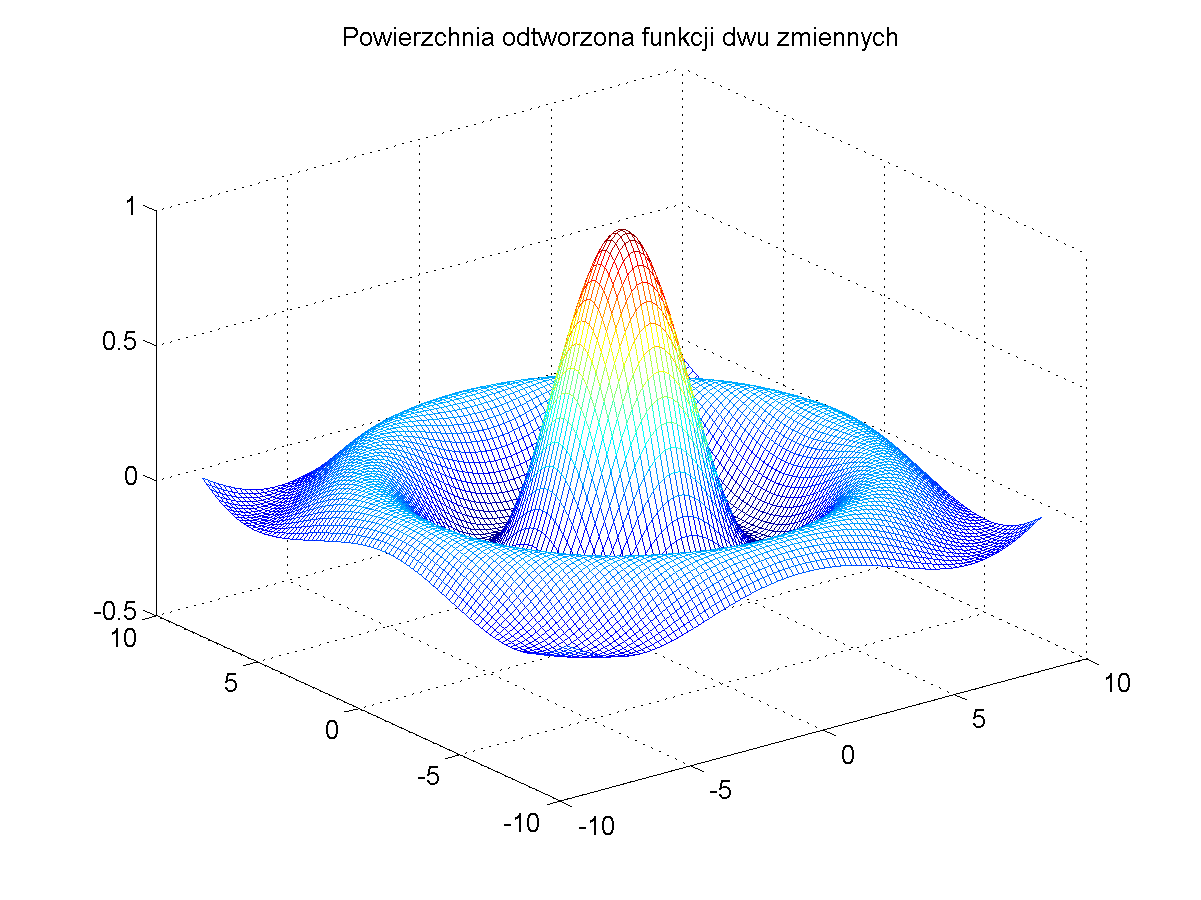
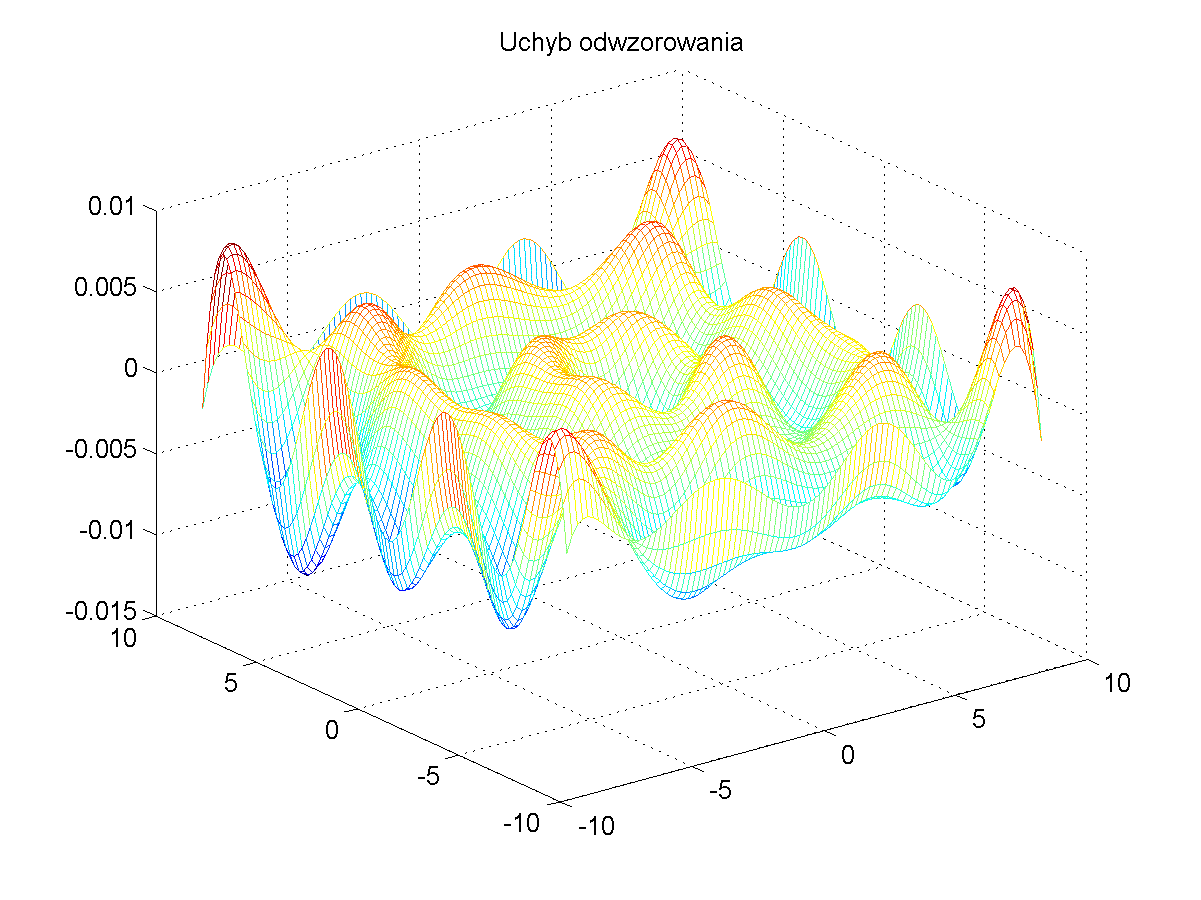
Rys. 4.5 Ilustracja odwzorowania funkcji nieliniowej przez sieć RBF: a) postać funkcji zadanej, b) położenia centrów funkcji radialnych, c) postać funkcji odtworzonej, d) błąd odtworzenia.

Jak widać odwzorowanie funkcji zadanej przez sieć RBF jest bliskie idealnemu. Błąd odwzorowania nie przekracza w całym zakresie wartości 0.01 i jest akceptowalny z praktycznego punktu widzenia.