Podręcznik
2. Sieci wektorów nośnych SVM
2.2. Sieć liniowa SVM w zadaniu klasyfikacji
Załóżmy, że dany jest zbiór par uczących \( (\mathbf{x}_i, d_i) \) dla \(i=1, 2, \ldots, p \) poddany klasyfikacji, w którym \( \mathbf{x}_i \) jest wektorem wejściowym a wartość zadana \( d_i \) jest równa \( 1 \) (klasa 1) bądź \( -1 \) (klasa przeciwstawna). Przy założeniu liniowej separowalności obu klas równanie hiperpłaszczyzny separującej może być zapisane wzorem
\( y(\mathbf{x})=\mathbf{w}^T\mathbf{x}+b=0 \)
w której \( \mathbf{w}=[w_1, w_2, \ldots, w_N]^T \) jest \(N\)-wymiarowym wektorem wag a \( \mathbf{x}=[x_1, x_2, \ldots, x_N]^T \), wektorem sygnałów wejściowych \( x_i \). Waga \(b\) stanowi polaryzację. Równania decyzyjne co do przynależności do klas przyjmują postać [68]
| \( \begin{aligned} \mathbf{w}^T \mathbf{x}_i+b > 0 & \rightarrow d_i=1 \\ \mathbf{w}^T \mathbf{x}_i+b < 0 & \rightarrow d_i=-1 \end{aligned} \) | (5.1) |
Za optymalną uważa się taką hiperpłaszczyznę \( y(\mathbf{x})=\mathbf{w}^T\mathbf{x}+b=0 \), która maksymalizuje margines separacji między dwoma klasami. Interpretacja marginesu separacji przedstawiona jest na rys. 5.1.
Odległość dowolnego punktu \( \mathbf{x}\) w przestrzeni wielowymiarowej od optymalnej hiperpłaszczyzny określona jest wzorem
| \( r(\mathbf{x})=\frac{y(\mathbf{x})}{\|\mathbf{w}\|} \) | (5.2) |
natomiast odległość początku układu współrzędnych od tej hiperpłaszczyzny jest szczególnym przypadkiem (\( \mathbf{x=0}\) ) i równa się \( r(\mathbf{0}) = b_0/\|\mathbf{w}\| \).
Na etapie uczenia wprowadza się pewien margines tolerancji rozdzielający obie klasy (nazywany marginesem separacji). Duża wartość tego marginesu zwiększa prawdopodobieństwo prawidłowej klasyfikacji dla danych testujących różniących się (z definicji) od danych uczących. Przy uwzględnieniu tolerancji i wprowadzeniu normalizacji warunek prawidłowego przypisania do klas można zapisać wówczas w postaci [68]
| \( \begin{aligned} \mathbf{w}^T \mathbf{x}_i+b \geq 1 & \rightarrow \quad d_i=1 \\ \mathbf{w}^T \mathbf{x}_i+b \leq -1 & \rightarrow \quad d_i=-1 \end{aligned} \) | (5.3) |
Oba równania można zapisać w pojedynczej postaci \( d_i\left(\mathbf{w}^T \mathbf{x}_i+b\right) \geq 1 \). Jeśli para punktów \( (\mathbf{x}_i, d_i) \) spełnia powyższe równanie ze znakiem równości to wektor \( \mathbf{x}_i \) tworzy tzw. wektor nośny \( \mathbf{x}_{sv} \)(ang. Support Vector - SV). Wektory nośne są tymi punktami danych, które leżą najbliżej optymalnej hiperpłaszczyzny i są najtrudniejsze w klasyfikacji. Co więcej przy założeniu pełnej separowalności liniowej danych należących do obu klas to one decydują o położeniu tej hiperpłaszczyzny i szerokości marginesu separacji, gdyż wszystkie punkty leżące z dala od hiperpłaszczyzny separującej spełniają warunek prawidłowej klasyfikacji z nadmiarem. Dla wektorów podtrzymujących \( \mathbf{x}_{sv} \) z definicji spełniony jest warunek \( \mathbf{w}^T\mathbf{x}_{sv} + b = \pm1 \) dla \( d(\mathbf{x}_{sv})=\pm1 \). Odległość wektorów podtrzymujących \( \mathbf{x}_{sv} \) od hiperpłaszczyzny określona jest zależnością
| \( r\left(\mathbf{x}_{s v}\right)=\frac{y\left(\mathbf{x}_{s v}\right)}{\|\mathbf{w}\|}=\left\{\begin{array}{ccc} \frac{1}{\|\mathbf{w}\|} & \text { dla } & g\left(\mathbf{x}_{sv}\right)=1 \\ -\frac{1}{\|\mathbf{w}\|} & \text { dla } & g\left(\mathbf{x}_{sv}\right)=-1 \end{array}\right. \) | (5.4) |
Margines separacji między obu klasami jest równy podwójnej wartości \( r(\mathbf{x}_{sv}) \), to znaczy
| \( \rho=2 r\left(\mathbf{x}_{sv}\right)=\frac{2}{\|\mathbf{w}\|} \) |
(5.5) |
Dla uzyskania efektu krzepkiej klasyfikacji, mało wrażliwej na szum występujący w danych pomiarowych, pożądana jest jak największa wartość tego marginesu. Z powyższego wzoru widać, że maksymalizacja marginesu separacji między dwoma klasami jest równoważna minimalizacji normy euklidesowej wektora wag \(\mathbf{w}\).
Problem uczenia liniowych sieci SVM, czyli doboru wag sieci dla danych uczących liniowo separowalnych sprowadza się do maksymalizacji marginesu separacji przy spełnieniu warunku (5.3). Nosi on nazwę problemu pierwotnego i zapisuje się go w postaci [68]
| \( \min \limits_w = \frac{1}{2}\mathbf{w}^T\mathbf{w} \) | (5.6) |
przy \( p \) liniowych ograniczeniach funkcyjnych \(i=1, 2, \ldots, p \)
| \( d_i\left(\mathbf{w}^T \mathbf{x}_i+b\right) \geq 1 \) |
(5.7) |
Jest to problem programowania kwadratowego z liniowymi ograniczeniami względem wag, który rozwiązuje się metodą mnożników Lagrange'a przez minimalizację tak zwanej funkcji Lagrange'a
| \( J(\mathbf{w}, b, \boldsymbol{\alpha})=\frac{1}{2} \mathbf{w}^T \mathbf{w}-\sum_{i=1}^p \alpha_i\left[d_i\left(\mathbf{w}^T \mathbf{x}_i+b\right)-1\right] \) | (5.8) |
w której wektor mnożników Lagrange'a \( \boldsymbol{\alpha} \) składa się z kolejnych mnożników \( \boldsymbol{\alpha}_i \) dla \(i=1, 2, \ldots, p \), o wartościach nieujemnych odpowiadających poszczególnym ograniczeniom, gdzie \( p \) oznacza liczbę par uczących. Mnożniki te rozszerzają liczbę parametrów optymalizowanych w procesie uczenia.
Rozwiązanie problemu minimalizacji funkcji Lagrange'a względem optymalizowanych parametrów \( \mathbf{w}, b, \boldsymbol{\alpha} \) jest określone przez punkt siodłowy funkcji Lagrange’a i odpowiada minimalizacji funkcji \( J(\mathbf{w}, b, \boldsymbol{\alpha}) \) względem wektora \(\mathbf{w},\) i parametru \( b \) oraz maksymalizacji względem wszystkich wartości mnożników tworzących wektor \(\boldsymbol{\alpha} \). Warunki optymalności rozwiązania względem \( \mathbf{w} \) i \( b \), są określone zależnościami
| \( \begin{aligned} & \frac{\partial J(\mathbf{w}, b, \boldsymbol{\alpha})}{\partial \mathbf{w}}=\mathbf{0} \quad \rightarrow \quad \mathbf{w}-\sum_{i=1}^p \alpha_i d_i \mathbf{x}_i=\mathbf{0} \\ & \frac{\partial J(\mathbf{w}, b, \boldsymbol{\alpha})}{\partial b}=0 \quad \rightarrow \quad \sum_{i=1}^p \alpha_i d_i=\mathbf{0} \end{aligned} \) | (5.9) |
Rozwiązanie powyższego układu równań przyjmuje postać
| \( \mathbf{w}=\sum_{i=1}^p \alpha_i d_i \mathbf{x}_i \) | (5.10) |
Dla wyznaczenia wartości b można wykorzystać fakt, że w punkcie siodłowym iloczyn mnożnika przez odpowiednie ograniczenie związane z wektorem \(\mathbf{x}_{sv} \) znika. Uwzględniając zależność \( \mathbf{w}^T\mathbf{x}_{sv} + b = \pm1 \) otrzymuje się
| \( b=\pm 1-\mathbf{w}^T\mathbf{x}_{sv} \) | (5.11) |
W przypadku doboru optymalnych wartości mnożników Lagrange’a uczenie sprowadza się do maksymalizacji funkcji Lagrange'a względem tych mnożników. Po wstawieniu zależności (5.10) i (5.11) do wzoru na funkcję Lagrange’a problem pierwotny przekształca się w problem dualny który można sformułować następująco [68]
| \( \max _{\boldsymbol{\alpha}} {Q}(\boldsymbol{\alpha})=\sum_{{i}=1}^{{p}} \alpha_{{i}}-\frac{1}{2} \sum_{{i}=1}^{{p}} \sum_{{j}=1}^{{p}} \alpha_{{i}} \alpha_{{j}} d_i d_j \mathbf{x}_i^T \mathbf{x}_j \) |
(5.12) |
przy ograniczeniach
| \( \begin{aligned}
\alpha_i & \geq 0 \\
\sum_{i=1}^p \alpha_i d_i & =0
\end{aligned} \) |
(5.13) |
dla \(i=1, 2, \ldots, p \). Rozwiązanie powyższego problemu optymalizacyjnego względem mnożników Lagrange'a pozwala wyznaczyć wartości optymalne wag w (równanie 5.10) i w następstwie również równanie określające sygnał wyjściowy \( y(\mathbf{x}) \) sieci (równy równaniu hiperpłaszczyzny separującej)
| \( y(\mathbf{x})=\sum_{i=1}^p \alpha_i d_i \mathbf{x}_i^T \mathbf{x}+b \) | (5.14) |
Przy rozwiązaniu problemu klasyfikacji wzorców nie w pełni separowalnych liniowo problem sprowadza się do określenia takiej optymalnej hiperpłaszczyzny, która minimalizuje prawdopodobieństwo błędu klasyfikacji na zbiorze uczącym z możliwie najszerszym marginesem separacji. W takim przypadku dane mogą naruszyć strefę marginesu separacji w dwojaki sposób.
-
Punkt danych \( (\mathbf{x}_i, d_i) \) położony jest wewnątrz strefy, ale po właściwej stronie optymalnej hiperpłaszczyzny. Nie występuje wówczas błąd klasyfikacji a jedynie realne zmniejszenie szerokości aktualnego marginesu.
-
Punkt danych \( (\mathbf{x}_i, d_i) \) położony jest wewnątrz lub na zewnątrz strefy, ale po niewłaściwej stronie optymalnej hiperpłaszczyzny. Odpowiada to wystąpieniu błędu klasyfikacji.
W rozwiązaniu problemu klasyfikacji danych nie separowalnych liniowo wprowadza się nieujemnie zdefiniowaną zmienną dopełniającą \( \xi \) zmniejszającą szerokość aktualnego marginesu separacji. Funkcje ograniczeń równościowych można wówczas zapisać w ogólniejszej postaci
| \( d_i\left(\mathbf{w}^T \mathbf{x}_i+b\right) \geq 1-\xi_i \) | (5.15) |
gdzie \( \xi_i \) jest nieujemną zmienną dopełniającą dobieraną indywidualnie dla każdej pary danych uczących. Jej wartość większa od zera efektywnie zmniejsza margines separacji, aż do jego przekroczenia, przy czym z definicji \( \xi_i \geq 0 \). Jeśli \( 0 \leq \xi_i \leq 1 \) to punkt danych \( (\mathbf{x}_i, d_i) \) leży wewnątrz strefy separacji po właściwej stronie. Jeśli natomiast \( \xi_i \geq 1 \) to punkt danych leży po niewłaściwej stronie optymalnej hiperpłaszczyzny i wystąpi błąd klasyfikacji. Wektory podtrzymujące spełniają dokładnie równanie \( d_i\left(\mathbf{w}^T \mathbf{x}_i+b\right) = 1-\xi_i \) a zatem uwzględnienie ich włącznie z tymi prowadzącymi do błędnej klasyfikacji ma wpływ na położenie optymalnej hiperpłaszczyzny. Uwzględnienie we wprowadzonych wcześniej ograniczeniach wyrażenia \( (1-\xi)_i \) zamiast wartości jednostkowej prowadzi do wzorów optymalizacyjnych o podobnej strukturze jak dla problemu klasyfikacji wzorców separowalnych liniowo. Przy klasyfikacji wzorców nie separowalnych liniowo problem pierwotny może więc być sprowadzony do minimalizacji zmodyfikowanej funkcji celu [59,68]
| \( \min _{\mathbf{w}} \frac{1}{2} \mathbf{w}^T \mathbf{w}+C \sum_{i=1}^p \xi_i \) | (5.16) |
przy ograniczeniach liniowych \(i=1, 2, \ldots, p \)
| \( \begin{aligned}
d_i\left(\mathbf{w}^T \mathbf{x}_i+b\right) & \geq 1-\xi_i \\
\xi_{\mathrm{i}} & \geq 0
\end{aligned} \) |
(5.17) |
Czynnik pierwszy we wzorze (5.16)) odpowiada maksymalizacji marginesu separacji, natomiast drugi odpowiada za przyszłe błędy testowania (suma \( \sum_{i=1}^p \xi_i \) jest maksymalnym, górnym oszacowaniem liczby tych błędów). Parametr \( C \) jest wagą z jaką traktowane są błędy testowania w stosunku do marginesu separacji, decydującą o złożoności przyszłej sieci neuronowej. Jest więc parametrem regularyzacyjnym, dobieranym przez użytkownika, na przykład w sposób eksperymentalny, poprzez trening połączony ze sprawdzaniem i oceną na bieżąco wyników. Postępując podobnie jak w przypadku wzorców separowalnych liniowo problem pierwotny jest sprowadzony do problemu dualnego, który można sformułować następująco [68] Dla danego zbioru danych uczących \( (\mathbf{x}_i, d_i) \) należy określić mnożniki Lagrange'a, które maksymalizują wartość funkcji błędu \( Q(\boldsymbol{\alpha}) \)
| \( \max \limits_{\boldsymbol{\alpha}} {Q}(\boldsymbol{\alpha})=\sum_{{i}=1}^{{P}} \alpha_{{i}}-\frac{1}{2} \sum_{{i}=1}^{{P}} \sum_{{j}=1}^{{P}} \alpha_{{i}} \alpha_{{j}} d_i d_j \mathbf{x}_i^T \mathbf{x}_j \) |
(5.18) |
przy ograniczeniach \(i=1, 2, \ldots, p \)
| \( \begin{aligned}
& 0 \leq \alpha_i \leq C \\
& \sum_{i=1}^p \alpha_i d_i=0
\end{aligned} \) |
(5.19) |
przy wartości \( C \) przyjętej z góry przez użytkownika. Ze sformułowania problemu wynika, że ani zmienna dopełniająca ani mnożniki Lagrange'a z nią związane nie pojawiają się w sformułowaniu problemu dualnego. Jedyna różnica w stosunku do problemu separowalności liniowej występuje w ograniczeniu górnym mnożników Lagrange'a. Mnożniki \( \alpha_i \) wynikające z rozwiązania zadania optymalizacyjnego (5.18) z ograniczeniami (5.19) muszą spełniać podstawowy warunek, mówiący że iloczyn mnożnika przez wartość funkcji ograniczenia dla każdej pary danych uczących jest równy zeru. Oznacza to, że wszystkie mnożniki dla których ograniczenie jest nieaktywne (ograniczenia spełnione z nadmiarem) muszą być równe zeru. Niezerowe wartości mnożników występują jedynie dla wektorów nośnych, dla których ograniczenie staje się typu aktywnego, ze znakiem równości (funkcja ograniczenia równa zeru).
Z rozwiązania problemu dualnego określa się wektor wag optymalnej hiperpłaszczyzny w postaci \( \mathbf{w}=\sum_{i=1}^p \alpha_i d_i \mathbf{x}_i \) identycznie jak dla problemu klasyfikacyjnego separowanego liniowo. Zauważmy, że sumowanie w powyższym wzorze dotyczy tylko składników uczących \(\mathbf{x}_i\), dla których mnożniki Lagrange'a są różne od zera. Są to tak zwane wektory nośne (podtrzymujące), których liczbę oznaczymy przez \( N_{sv} \). Jak z powyższego wzoru widać równanie optymalnej hiperpłaszczyzny zależy wyłącznie od wektorów nośnych. Pozostałe wektory ze zbioru danych uczących nie mają żadnego wpływu na wynik rozwiązania.
Równanie określające sygnał wyjściowy \( y(\mathbf{x}) \) sieci liniowej SVM o wagach optymalnych wynika ze wzoru (5.14), które tutaj przepiszemy w postaci
| \( y(\mathbf{x})=\sum_{i=1}^{N_{\text {sv }}} \alpha_i d_i \mathbf{x}_i^T \mathbf{x}+b \) | (5.20) |
Jest to równanie liniowe względem zmiennych wejściowych opisanych wektorem \( \mathbf{x} \) i wagach uzależnionych od niezerowych mnożników Lagrange'a i odpowiadających im wektorów podtrzymujących \( \mathbf{x}_i \) oraz wartości zadanych \( d_i\) stowarzyszonych z nimi.

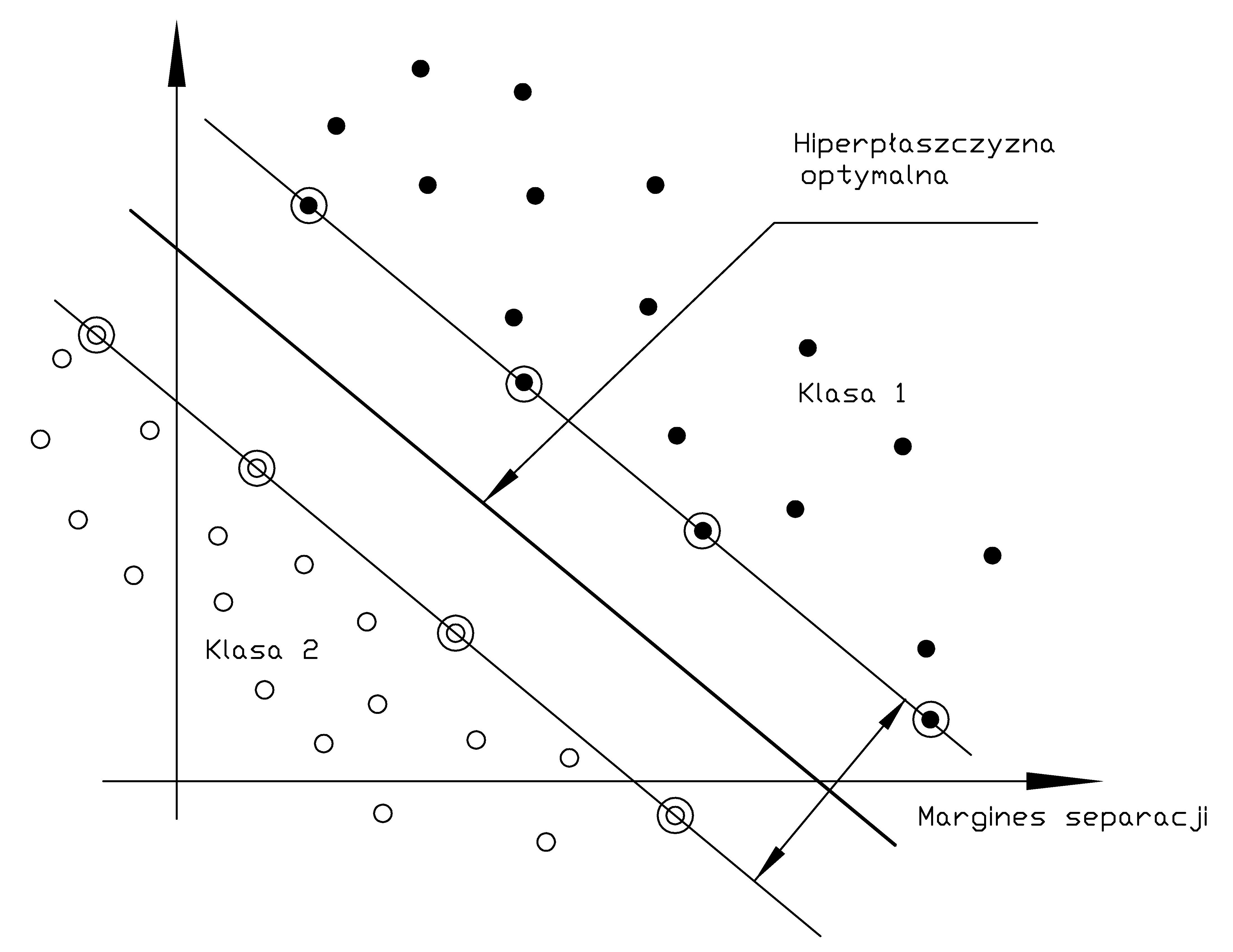
Na rys. 5.2 przedstawiono wynik klasyfikacji danych należących do dwu klas przy zastosowaniu liniowej sieci SVM uzyskany pry użyciu programu Gunna [21]. Wobec niepełnej separowalności danych uczących sieć liniowa dokonała klasyfikacji z 2 błędami (po jednym błędnym przypisaniu do każdej z klas). Margines separacji uwzględnia zmniejszenie odstępu od hiperpłaszczyzny separującej o wartości zmiennych dopełniających. Każdy punkt danych znajdujący się wewnątrz marginesu separacji oraz na obu hiperpłaszczyznach wektorów nośnych tworzy wektor podtrzymujący. W sumie jest ich 5, co stanowi 13.9% ogólnej liczby danych.
