Podręcznik
3. Sieci neuronowe głębokie
3.2. Sieć konwolucyjna CNN
Sieci konwolucyjne (ang. Convolutional Neural Networks – CNN) zwane również sieciami splotowymi powstały jako narzędzie analizy i rozpoznawania obrazów wzorowane na sposobie działania naszych zmysłów [18,37]. Wyeliminowały kłopotliwy i trudny dla użytkownika etap manualnego opisu cech charakterystycznych obrazów, stanowiących atrybuty wejściowe dla końcowego etapu klasyfikatora bądź układu regresyjnego. W tym rozwiązaniu sieć sama odpowiada za generację cech. Poszczególne warstwy sieci CNN przetwarzają obrazy z warstwy poprzedzającej (na wstępie jest to zbiór obrazów oryginalnych) poszukując prymitywnych cech (np. grupy pikseli o podobnym stopniu szarości, krawędzie, przecinające się linie itp.). Kolejne warstwy ukryte generują pewne uogólnienia cech z warstwy poprzedzającej organizowane w formie obrazów. Przykład wyników takiego przetworzenia obrazu kolorowego w warstwie ukrytej sieci zawierającej 48 neuronów (każdy wielowejściowy o różnych wartościach wag) pokazano na rys. 6.1. Kolejny kwadrat obrazu wynikowego przedstawia cechy diagnostyczne (w formie podobrazu) utworzone przez każdy z tych neuronów.

Obrazy te w niczym nie przypominają oryginałów, ale reprezentują cechy charakterystyczne dla nich wyrażone w formie szarości pikseli. W efekcie kolejnego wielowarstwowego przetwarzania obrazów z poprzedniej warstwy ostatnia warstwa konwolucyjna generuje obrazy stosunkowo niewielkich wymiarów reprezentujące cechy charakterystyczne dla przetwarzanego zbioru. Obrazy te w poszczególnych warstwach są reprezentowane przez tensory, których elementy są następnie przetwarzane na postać wektorową, będącą początkiem układu w pełni połączonego (ang. fully connected – FC), stanowiącego właściwy klasyfikator bądź układ regresyjny. Przykład takiej struktury CNN przedstawiono na rys. 6.2 [46].
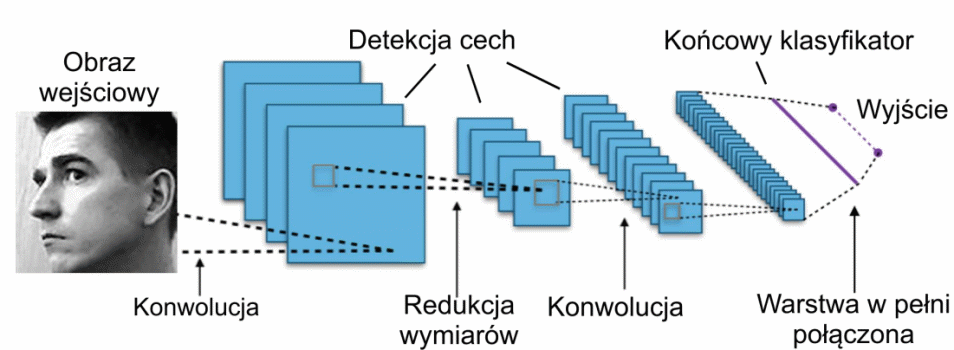
Kolejne warstwy sieci mają zadanie wygenerować w sposób automatyczny (całkowicie poza udziałem człowieka) zbiór cech charakterystycznych dla analizowanych wzorców obrazowych, który następnie podlegają klasycznemu przetworzeniu w decyzję klasyfikacyjną bądź regresyjną.
6.2.2 Podstawowe operacje w sieci CNN
Nazwa sieci CNN pochodzi od operacji splotu (konwolucji) stanowiącej istotny element procesu obliczeniowego. W przypadku obrazów tablica danych jest reprezentowana przez dwuwymiarową macierz \( \mathbf{I} \) o elementach reprezentujących stopnie jasności pikseli \( I(m,n) \) a jądro \( \mathbf{K} \) jest dwuwymiarowe. Operacja splotu dwuwymiarowego jest wówczas zapisana w postaci [18,38]
| \( Y(i, j)=I(i, j) * K(i, j)=\sum_m \sum_n I(m, n) K(i-m, j-n)=\sum_m \sum_n I(i-m, j-n) K(m, n) \) | (6.1) |
W sieciach CNN wejściem dla pierwszej warstwy ukrytej jest zwykle reprezentacja RGB obrazów ustawionych w formie tensora. Operacja konwolucji w pierwszej warstwic konwolucyjnej obejmuje wszystkie trzy kanały RGB obrazu (suma poszczególnych kanałów), każdy z innymi przyjętymi wartościami wag jądra w postaci filtru liniowego stanowiącego neuron analizujący. W dalszych warstwach operacja ta obejmuje wiele (ustalonych przez użytkownika) obrazów z warstwy poprzedzającej (tak zwana konwolucja grupowa).
Przykład operacji konwolucyjnej dla kroku przesunięcia filtru (stride) równego 2 przedstawiono na rys. 6.3 [34]. Dane wejściowe stanowią 3 kanały RGB obrazu. Każdy kanał jest przetwarzany przez odpowiedni dla niego filtr (neuron) a wyniki przetworzenia sumowane z uwzględnieniem polaryzacji tworząc obraz wynikowy. W efekcie, w każdej warstwie konwolucyjnej filtr jest wielowymiarowy, realizujący operacje tensorowe, przy czym wymiar maski filtrującej jest równy \( n_x \times n_y \), a liczba tych masek tworzących jeden filtr jest równa liczbie obrazów wejściowych dla danej warstwy podlegających przetworzeniu (maksymalnie liczba obrazów poprzedniej warstwy). W przypadku pierwszej warstwy konwolucyjnej i obrazowi reprezentowanemu przez 3 kanały RGB każdy filtr składa się z trzech jednostek (patrz filtr \( W0 \) lub \( W1 \)). Liczba obrazów wyjściowych po konwolucji jest równa liczbie zastosowanych filtrów wielokanałowych (w prykładzie są 2 filtry \( W0 \) i \( W1 \)), stąd 2 obrazy wyjściowe reprezentowane na rysunku przez Output Volume.
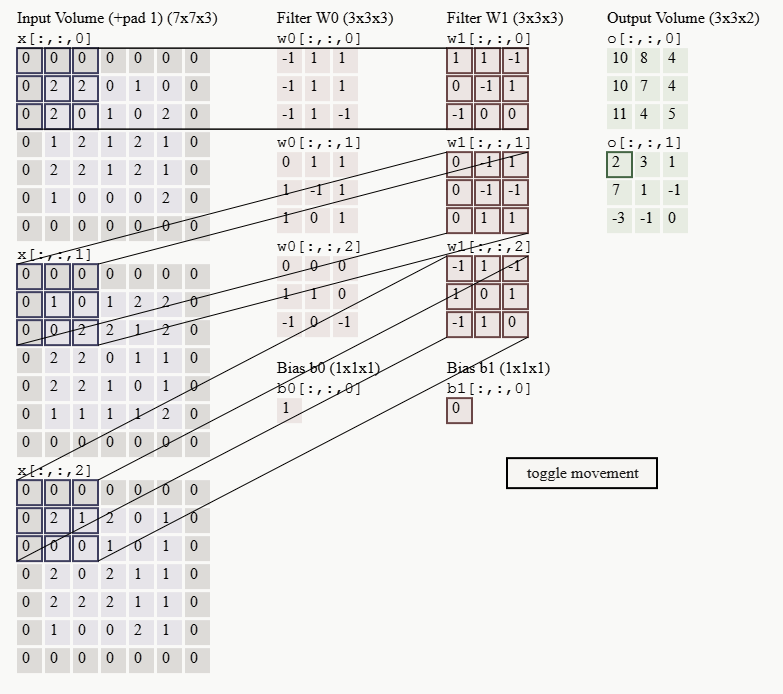
W przetwarzaniu danych operacja konwolucji stosowana w CNN charakteryzuje się ważnymi zaletami w stosunku do zwykłych operacji macierzowych w sieciach klasycznych. Należą do nich: lokalność połączeń, wspólne (powtarzalne) wartości wag połączeń filtru przesuwającego się po obrazie i powstała dzięki temu niezmienniczość (ekwiwariancja) względem przesunięcia.
Każdy sygnał wyjściowy filtru podlega działaniu nieliniowej funkcji aktywacji, która w przypadku CNN przybiera najczęściej postać ReLU (ang. Rectified Linear Unit) opisaną wzorem [18, 78]
| \( y(x)=\left\{\begin{array}{lll} x & \textrm{dla} & x \ge 0 \\ 0 & \textrm{dla} & x \le 0 \end{array}\right. \) | (6.2) |
Funkcja ta charakteryzuje się nieciągłą pochodną. Ten fakt może utrudnić uczenie sieci metodami gradientowymi. Stąd często zastępuje się ją aproksymacją zwaną softplus, zdefiniowaną następująco [18]
| \( y(x) = \ln( 1 + e^x) \) | (6.3a) |
Jej pochodna jest ciągła i reprezentuje sigmoidę unipolarną. W wyniku konwolucji i działania funkcji ReLU uzyskuje się wartości reprezentujące stopień szarości pikseli obrazu wynikowego.
W niektórych implementacjach sieci głębokich, na przykład w GAN stosuje się zmodyfikowaną funkcję aktywacji LReLU (ang. Leaky ReLU), w której w części ujemnej charakterystyki wartości zerowe zastępuje się linią prostą o małym nachyleniu \( a \). Funkcję taką opisuje się wzorem
| \( y(x)=\left\{\begin{array}{lll}
x & \textrm{dla} & x \ge 0 \\
ax & \textrm{dla} & x \le 0
\end{array}\right. \) |
(6.3b) |
przy wartości \(a<1\); typowa wartość to \(a=0.01\).
Stosowana jest również wersja wykładnicza funkcji ReLU, zwana w skrócie ELU (ang. exponential linear unit), która definiowana jest wzorem
| \( y(x)=\left\{\begin{array}{lll} x & \textrm{dla} & x \ge 0 \\ a(e^x -1) & \textrm{dla} & x \le 0 \end{array}\right. \) | (6.3c) |
w którym \( a \) jest hiperparametrem o wartości dodatniej, ułamkowej (typowa wartość \(a=0.01 \)). Badania pokazały, że dzięki zastosowaniu takiej funkcji można uzyskać lepszą dokładność klasyfikatora CNN.
Liczba neuronów konwolucyjnych, filtrujących poszczególne obszary lokalne obrazu ustalana jest przez użytkownika. Każdy neuron (filtr) ma określoną przez użytkownika liczbę wag podlegających doborowi i łączących go z określonym rejonem lokalnym obrazu. Dla typowych wielkości maski 3x3 (małe obrazy) lub 5x5 (obrazy duże) liczba wag neuronu (liczba elementów filtru) staje się więc równa 9 lub 25 (plus waga polaryzacji). Stosuje się również maski punktowe, o wymiarze 1x1. Taka wielkość maski zdecydowanie zmniejsza liczbę adaptowanych parametrów sieci.
Przesuwna maska analizy wędrująca po obrazie wejściowym dostarcza do wyjścia sygnał sumacyjny będący sumą iloczynów jasności pikseli i odpowiednich, połączonych z nimi wag neuronu (wartości elementów filtru) na zasadzie konwolucji. Neuron ze swoimi wagami stanowi więc filtr o stałych parametrach przesuwany po obrazie z określonym krokiem. Przesuwanie maski filtracyjnej neuronu sterowane jest przez wybór wielkości kroku stride. Wielkość stride=1 oznacza, że nowa maska przesuwana jest o jeden piksel obrazu (w kierunku \(x \) lub \( y \)) w stosunku do pozycji poprzedniej maski. Rozmiar obrazu wynikowego zależy od wybranego kroku stride i wielkości maski filtrującej.
W następnym kroku powstały obraz wynikowy poddaje się działaniu operacji łączenia sąsiednich wyników, tzw. operacja „pooling”, redukując w ten sposób wymiar obrazów. Funkcja ta przekształca wynik nieliniowego działania filtracyjnego neuronu w określonym rejonie obrazu poprzez zdefiniowaną statystykę dotyczącą najbliższych mu pikseli pod względem lokalizacji wyników wyjściowych. Typowe funkcje to: max pooling zwracająca wartość maksymalną wyników neuronów znajdujących się w sąsiedztwie prostokątnym aktualnego wyniku oraz average pooling zwracającą wartość średnią wyników w tym obszarze. Przykład takiej operacji uwzględniającej obszar maski 2x2 przedstawiony jest na rys. 6.4.
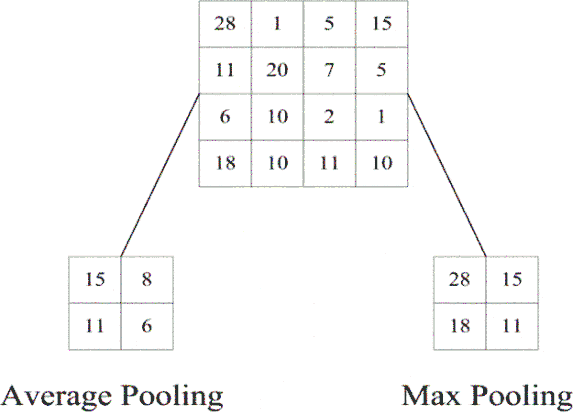
Operacja pooling poza zmniejszeniem wymiaru obrazu pozwala uzyskać reprezentację bardziej inwariantną względem niewielkiego przemieszczenia danych. Stanowi pewne uogólnienie cech reprezentowanych przez sąsiednie grupy pikseli. Często dla zachowania odpowiednich wymiarów obrazu stosuje się operację uzupełnienia brzegów zerami tzw. „zero padding”. Zwykle jest to uzupełnienie symetryczne z obu stron obrazu.
Dodatkowo stosuje się również normalizację stopnia szarości obrazów powstałych w wyniku konwolucji. Najczęściej jest to to operacja stosowana na danych „mini-batch” (małego zestawu danych wybranego losowo aktualnie z pełnego zbioru używanego w operacji konwolucji). Wykonywana jest na bezpośrednich wynikach konwolucji liniowej (po operacji ReLU). Odbywa się poprzez odjęcie wartości średniej i podzieleniu takich wyników przez odchylenie standardowe danych zawartych w „mini-batch” od rzeczywistych wartości obrazu otrzymanych z konwolucji.
Liczba neuronów konwolucyjnych, filtrujących poszczególne obszary lokalne obrazu ustalana jest przez użytkownika i decyduje o liczbie obrazów wynikowych. Wymiar obrazu wynikowego filtracji zależy od wielkości kroku stride, wielkości maski filtrującej i zastosowanego uzupełnienia zerami. Istnieje ścisła relacja wiążąca rozmiar wynikowy O obrazu z rozmiarem obrazu wejściowego W, wielkością filtru F, kroku stride S i wielkością uzupełnienia zerami z obu stron symetrycznie (zero padding P). Wielkości te są powiązane relacją [18]
| \( O=(W−F+2P)/S+1 \) | (6.4) |
określającą wymiar obrazu wyjściowego. Przykładowo, jeśli obraz wejściowy ma wymiar \(7\times 7\) (\(W=7\)), zastosowany filtr \(3\times 3\) (\(F=3\)), stride \(S=1\) oraz \(P=0\) wówczas otrzymuje się obraz wyjściowy o wymiarze \( 5\times 5 \), gdyż \(O=(7-3)/1+1=5 \). Podobnie dla \(S=2\) otrzymuje się wymiar obrazu wyjściowego równy \(3\times 3\).
Przykład graficzny wpływu wielkości kroku stride na wynik operacji w przypadku danych wejściowych jednowymiarowych o 7 elementach (\(W=7\)) przedstawiono na rys. 6.5. W obu przypadkach neuron filtrujący ma trzy połączenia wagowe (\(F=3\)) o wartościach wag równych kolejno: \(1, 0, -1\) oraz brak uzupełnienia zerami (\(P=0\)). Wynik przedstawiony jest dla 2 różnych wartości parametru stride. W pierwszym przypadku jest to wartość stride=1, w drugim stride=2. W zależności od wyboru otrzymuje się różną liczbę elementów wynikowych: w pierwszym przypadku jest to 5 wyników, w drugim tylko trzy.
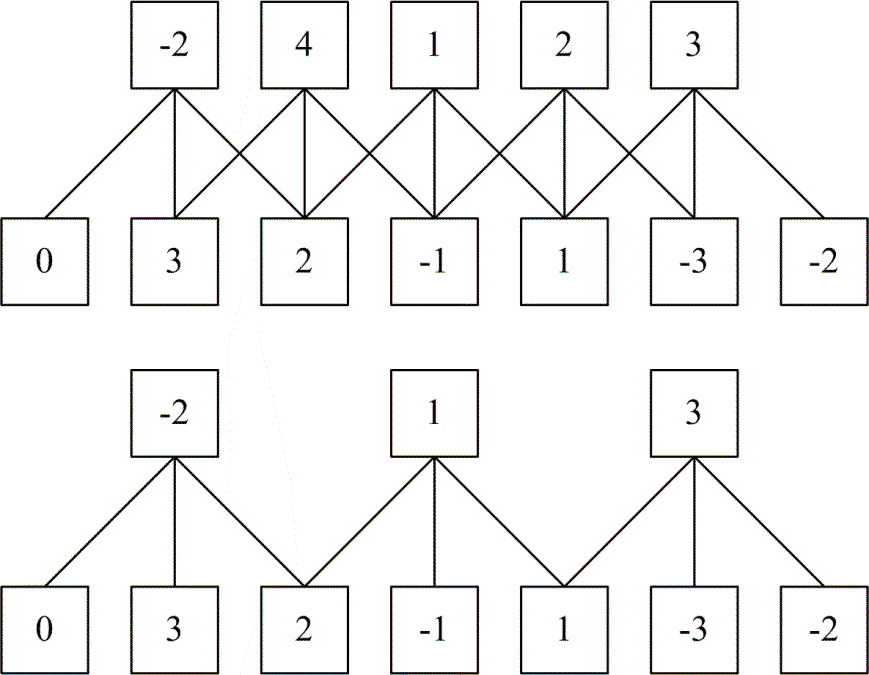
Zdefiniowane wartości parametrów mają ważne znaczenie przy projektowaniu struktur CNN, gdyż niewłaściwie przyjęte liczby mogą prowadzić do niecałkowitych wartości rozmiarów obrazów wejściowych. Przykładowo w architekturze ALEXnet Krizhevskiego [34] wymiar wejściowy obrazów jest równy \(227\times227\times3\) (reprezentacja RGB). Zastosowane przez niego wymiary w pierwszej warstwie ukrytej to \(F=11, S=4, P=0\). Stąd wymiar obrazu wyjściowego po konwolucji jest równy \(O=(227-11)/4+1=55\), czyli obraz \(55\times55\). Gdyby wymiar obrazu wejściowego był równy na przykład \(224\times224\) wówczas wymiar obrazu wyjściowego przy \(S=4\) po konwolucji nie byłby liczbą całkowitą, gdyż wówczas \(O=(224-11)/4+1=54,25\), co blokuje dalszy proces przetwarzania.
W poszczególnych warstwach ukrytych obrazy wynikowe tworzą tensory (strukturę trójwymiarową reprezentowaną przez dwa wymiary obrazu i liczbę przetwarzanych obrazów). Obrazy (macierze) ostatniej warstwy konwolucyjnej są przetwarzane na postać wektorową, stanowiącą początek sieci w pełni połączonej w której każdy neuron jest połączony z każdym sygnałem warstwy poprzedniej – połączenia globalne (ang. Fully Connected layer – FC). Neurony w warstwie o pełnym połączeniu mają unikane wagi, podlegające adaptacji w procesie uczenia.
Przejście z reprezentacji tensorowej (wiele obrazów m-wymiarowych) na postać wektorową (pojedyncze sygnały wektora tworzące wejście dla właściwego klasyfikatora) może odbywać się na wiele sposobów. Jednym z nich jest przyjęcie wszystkich wartości pikselowych poszczególnych obrazów jako cech diagnostycznych i ustawienie ich w formie wektora poprzez operację tzw. reshape. Przy zbyt dużych wymiarach obrazów stosowane może być zmniejszenie rozdzielczości obrazów tensora. Innym rozwiązaniem jest zastosowanie operacji pooling z odpowiednim krokiem stride. W niektórych przypadkach można zaprojektować sieć w taki sposób, że ostatnia warstwa konwolucyjna zawiera tylko pojedynczą wartość dla każdego kanału.
W większości rozwiązań sieci CNN użytej jako klasyfikatora zamiast klasycznej wielowarstwowej sieci neuronowej stosuje się klasyfikator typu softmax, w którym sygnały wejściowe są bezpośrednio przetwarzane na prawdopodobieństwo przynależności do określonej klasy [18]. Liczba neuronów wyjściowych jest równa liczbie klas przy czym każdy neuron podlega adaptacji wag w klasyczny sposób poprzez optymalizację funkcji celu zdefiniowanej w postaci entropii krzyżowej (ang. cross entropy). Wartość sygnału sumacyjnego neuronu \(i\)-tego określona jest wówczas wzorem
| \( u_i(x)=\sum_j w_{i j} x_j+w_0 \) | (6.5a) |
Prawdopodobieństwo przynależności wektora \( \mathbf{x} \) do \(i\)-tej klasy (\(i=1, 2, …, M\)) zależy od wartości funkcji softmax obliczanej dla każdej składowej wektora wyjściowego według wzoru
| \( \operatorname{softmax}\left(u_i\right)=\frac{\exp \left(u_i\right)}{\sum_{j=1}^M \exp \left(u_j\right)} \) | (6.5b) |
Wartość największa funkcji wyznacza przynależność do klasy określonej wskaźnikiem \( i \).
Przystępując do uczenia sieci CNN należy w pierwszej kolejności ustalić liczbę warstw ukrytych (konwolucyjnych), pełniących rolę ekstraktora cech procesu, liczbę neuronów w poszczególnych warstwach (każdy odpowiedzialny za wytworzenie pojedynczego obrazu), wielkość maski filtracyjnej neuronu i związanej z tym liczby połączeń wagowych, rodzaj funkcji aktywacji, wielkość parametru stride w każdej warstwie oraz wybór parametru zero-padding.
Proces uczenia sieci polega na adaptacji parametrów zarówno filtrów w części lokalnie połączonej, jak i wartości wag klasyfikatora końcowego (struktura w pełni połączona). W przypadku warstw ukrytych polega na doborze wag przesuwających się filtrów. Liczba tych wag zależy od przyjętej wielkości maski filtracyjnej. Wielkość maski w przypadku obrazów zależy od ich wielkości. Przy małych obrazach typowy wymiar to \(5\times 5\) (25 wag neuronu), przy dużych - wielkość stosowanej maski może być nawet \(11\times 11\) (121 wag neuronu). Każdy neuron w warstwie powinien wykrywać inne szczegóły obrazu, np. układ pikseli tworzący krawędzie w określonym kierunku, skupienia pikseli tworzące plamki, zmiany jasności w regionie, itp. W procesie uczenia pierwotnego liczba adaptowanych parametrów filtrów w części sieci lokalnie połączonej dominuje w ogólnej populacji zmiennych podlegających optymalizacji.
Uczenie sieci odbywa się to poprzez minimalizację funkcji kosztu. Funkcja kosztu może być definiowana w różny sposób. W sieciach głębokich pełniących rolę klasyfikatora najczęściej stosowana jest definicja kross-entropijna (ang. cross-entropy function), bazująca na prawdopodobieństwie przynależności do określonej klasy, przy czym to prawdopodobieństwo określane jest poprzez znormalizowaną funkcję sigmoidalną zwaną softmax zdefiniowana wzorem (6.5), przy czym największa wartość prawdopodobieństwa wyznacza ostateczną przynależność do jednej spośród M klas. Oznaczmy wartość funkcji softmax w postaci \(f(u_i)\) [18]
| \( f\left(u_i\right)=\frac{\exp \left(u_i\right)}{\sum_{j=1}^n \exp \left(u_j\right)} \) | (6.6) |
Zmienna \(u_i\) w tym wzorze jest sumą wagową sygnałów dopływających do \(i\)-tego neuronu wyjściowego. W zdaniach klasyfikacji wieloklasowej (\(M\) klas) tylko jedna klasa jest prawdziwa (etykieta tej klasy \(d=1\)). Pozostałe klasy mają etykietę \(d=0\). Zatem w procesie uczenia tylko klasa wskazana przez sieć jako prawdziwa bierze udział w obliczaniu funkcji błędu (kosztu) przyjmując \(d=1\). Pozostałe wyjścia mają etykiety \(d=0\) i nie biorą bezpośredniego udziału w definicji funkcji celu. Entropijna (logarytmiczna) definicja funkcji celu zapisana w postaci ogólnej
| \( E=-\sum_{i=1}^{M} d_i \log \left(f\left(u_i\right)\right) \) |
(6.7) |
Wobec tylko jednej wartości \( d_i=d_p\) różnej od zera (równej \(1\)) dla klasy "pozytywnej" może być uproszczona do postaci
| \( E=-\log \left(f(u_i)\right)=-\log \left|\frac{\exp \left(u_i \right)}{\sum_{i=1}^M \exp \left(u_i\right)}\right| \) | (6.8) |
Składniki funkcji celu względem klas “negatywnych” są równe zeru. Tylko klasa wskazana przez sieć bierze bezpośredni udział w tworzeniu funkcji celu. Tym niemniej gradient funkcji celu zależy również od składników klas „negatywnych”, ze względu na postać mianownika w wyrażeniu (6.18). Należy przy tym zauważyć, że składniki gradientu funkcji celu względem sygnału sumacyjnego \(u_n\) dla klas „negatywnych” będą miały identyczną postać, wyrażoną wzorem
| \( \frac{\partial}{\partial u_n}\left(-\log \left(\frac{\exp \left(u_p\right)}{\sum_{j=1}^M \exp \left(u_j\right)}\right)\right)=\frac{\exp \left(u_n\right)}{\sum_{j=1}^M \exp \left(u_j\right)} \) |
(6.9a) |
natomiast dla klasy "pozytywnej", wskazanej przez sieć wyrażenie (sygnał sumacyjny \(u_p\)) będzie miało postać
| \( \frac{\partial}{\partial u_p}\left(-\log \left(\frac{\exp \left(u_p\right)}{\sum_{j=1}^M \exp \left(u_j\right)}\right)\right)=\frac{\exp \left(u_p\right)}{\sum_{j=1}^M \exp \left(u_j\right)}-1 \) | (6.9b) |
Znając wektor gradientu względem poszczególnych sygnałów składniki gradientu względem poszczególnych wag \(w\) występujących w wyrażeniu (6.5) na sygnał sumacyjny są wyznaczane korzystając z własności różniczkowania funkcji złożonej, mianowicie
| \( \frac{\partial E}{\partial w_i}=\frac{\partial E}{\partial u} \frac{\partial u}{\partial w_i}=\frac{\partial E}{\partial u} x_i \) | (6.10) |
Najczęściej stosowanym algorytmem w uczeniu sieci CNN jest stochastyczny algorytm największego spadku z momentem rozpędowym (ang. Stochastic Gradient Descent – SGDM) [18,43]. Adaptacja wag odbywa się iteracyjnie zgodnie ze wzorem
| \( \mathbf{w}(k)=\mathbf{w}(k-1)-\eta \mathbf{g}(k-1)+\alpha[\mathbf{w}(k-1)-\mathbf{w}(k-2)] \) | (6.11) |
w którym \(\alpha\) jest współczynnikiem momentu przyjmowanym z przedziału \([0, 1]\). Dla przyśpieszenia procesu uczenia w poszczególnych iteracjach zamiast pełnego zbioru danych uczących używa się losowo wybranego podzbioru (tzw. minibatch). Powstało wiele modyfikacji tego algorytmu przyśpieszających proces uczenia, z których najczęściej używany (między innymi w Matlabie) jest ADAM (skrót of ang. ADAptive Momenet estimation) [43]. W odróżnieniu od SGD w tej metodzie każdy parametr \(w\) ma adaptacyjnie dobierany współczynnik uczenia uzależniony od momentu statystycznego gradientu pierwszego i drugiego rzędu. Momenty te dla optymalizowanej zmiennej \(w\) definiowane są w postaci średniej kroczącej
-
moment pierwszego rzędu (start z wartości zerowych)
| \( m_w(k)=\beta_1 m_w(k-1)+\left(1-\beta_1\right) g(k) \) | (6.12) |
-
moment drugiego rzędu
| \( v_w(k)=\beta_2 v_w(k-1)+\left(1-\beta_2\right) g^2(k) \) | (6.13) |
gdzie \(\beta_1\) i \(\beta_2\) są hiperparametrami dobieranymi przez użytkownika, zwykle w zakresie \([0.9 – 0.999]\). Na tej podstawie oblicza się estymatę nieobciążoną obu momentów, używaną w adaptacji poszczególnych wag sieci
| \( \hat{m}_w(k)=\frac{m_w(k)}{1-\beta_1^k} \) | (6.14) |
| \( \hat{v}_w(k)=\frac{v_w(k)}{1-\beta_2^k} \) | (6.15) |
Adaptacja wagi \( w\) następuje według wzoru
| \( w(k)=w(k-1)-\eta \frac{\hat{m}_w(k)}{\sqrt{\hat{v}_w(k)}+\varepsilon} \) | (6.16) |
Eksperymenty numeryczne wykazały znaczące przyspieszenie procesu uczenia przy zastosowaniu adaptowanego współczynnika dla każdej wagi. Tym niemniej nie zawsze jakość uzyskanych wyników jest lepsza niż algorytmu SGDM.
Bezpośrednie podejście do adaptacji wszystkich wag przy zastosowaniu globalnej metody propagacji wstecznej uczenia dla całej sieci jest kosztowne obliczeniowo, gdyż wiąże się z ogromną liczbą dobieranych parametrów. Przyśpieszenie procesu uczenia jest możliwe poprzez dobór wstępny wag filtrów warstw konwolucyjnych przy zastosowaniu różnego rodzaju rozwiązań techniki uczenia bez nauczyciela. Stosowane są różne podejścia do tego problemu.
-
Inicjalizacja losowa wag każdego neuronu w każdej warstwie konwolucyjnej. Metoda ta jest znana i przebadana w przypadku klasycznych sieci neuronowych typu ELM (Extreme Learning Machine).
-
Inicjalizacja manualna wykorzystująca doświadczenie użytkownika, ukierunkowana na przykład na wykrywanie krawędzi w określonym kierunku. Można tu zastosować wstępnie klasyczne liniowe filtry cyfrowe obrazu, np. filtry Sobela, Previtta, Canny, Log, itp.
-
Inicjalizacja poprzez grupowanie danych, na przykład przy pomocy algorytmu k-means. W metodzie tej grupowanie przeprowadza się dla losowo wybranych małych fragmentów obrazu i parametry centroidu przyjmuje się jako wartości wag neuronów filtracyjnych.
-
Inicjalizacja poprzez wstępne uczenie zachłanne (greedy learning) z nauczycielem, warstwa po warstwie (najpierw warstwa pierwsza, potem warstwa druga na bazie wyników przetworzenia sygnałów przez warstwę pierwszą itd.). Stosowane są różne warianty tego rozwiązania, pozwalające na znaczne przyśpieszenie procesu uczenia. Po wstępnym doborze wag następuje zwykle douczenie pełnej sieci przy wykorzystaniu metody największego spadku i propagacji wstecznej błędu.
Przy obecnym stanie równoległej techniki obliczeniowej i zastosowaniu procesora graficznego możliwe stało się zastosowanie uczenia z nauczycielem do pełnej (losowo zainicjowanej) sieci w każdej iteracji uczącej (ekstremalne podejście do uczenia). Tym nie mniej przy zastosowaniu takiego podejścia należy się liczyć z długotrwałym procesem uczenia, zwłaszcza jeśli wymiary obrazów wejściowych są duże.
Najczęściej stosowanym podejściem w praktyce inżynierskiej przy tworzeniu sieci CNN jest zastosowanie tzw. metody transfer learning. W tym podejściu korzysta się ze wstępnie nauczonej sieci dostępnej między innymi w Matlabie, o parametrach dobranych przez specjalistów. Użytkownik dokonuje jedynie adaptacji określonej części struktury sieci (zwykle klasyfikatora końcowego) na swoich danych. Parametry warstw odpowiedzialnych za mechanizm generacji cech diagnostycznych pozostają często zamrożone. Uczenie takie odbywa się metodami gradientowymi z zastosowaniem propagacji wstecznej błędu i przebiegają stosunkowo szybko.
W ostatnich implementacjach Matlaba (poczynając od 2016 roku) dostępne są m-pliki do uczenia i testowania sieci CNN. Sposób wykorzystania tych podprogramów można uzyskać przy pomocy komendy help cnn. Użytkownik po wczytaniu danych uczących i testujących definiuje architekturę sieci (liczbę warstw i neuronów warstwie, funkcję aktywacji, rodzaj funkcji pooling, etc.), opcje wyboru parametrów uczenia, następnie dokonuje procesu uczenia (funkcja trainNetwork) i następnie testowania (funkcja classify).
Dane uczące i testujące przygotowane są w postaci tablicy 3-D dla obrazów w skali szarości lub 4-D dla obrazów reprezentowanych w postaci RGB. Pierwsze 2 współrzędne zawierają wartości pikseli w osi x i y obrazu, trzecia współrzędna (przy reprezentacji 4-D) jest równa 1, 2 lub 3 prezentując obraz R, G lub B a ostatnia nr kolejny obrazów w bazie. Dane dotyczące klasy reprezentowanej przez obraz są kodowane numerycznie (klasa 1, 2, 3, itd.) w postaci wektorowej.
