Podręcznik
3. Sieci neuronowe głębokie
3.9. Autoenkoder wariacyjny
6.9.1 Podstawy działania
Autoencoder wariacyjny (ang. variational autoencoder - VAR) jest innym rozwiązaniem sieci głębokiej umożliwiającym generację obrazów podobnych do oryginału [33,76,77]. Będzie dalej oznaczany skrótem VAR. Sieć taka działa na innych zasadach niż przedstawiona wcześniej sieć klasycznego autoenkodera (AE). Nazwa sieci wywodzi się z bliskiej relacji mechanizmu działania z zasadą regularyzacji sieci i wnioskowania wariacyjnego w statystyce.
Sieć VAR wykorzystuje w swoim działaniu zasadę redukcji wymiarowości danych, tak przeprowadzoną, że możliwe jest odtworzenie danych oryginalnych z określoną dokładnością przy zachowaniu w miarę wiernego odwzorowania rozkładu statystycznego (wartości średniej i wariancji) w poszczególnych rejonach obrazu. Redukcja wymiarowości danych oznacza reprezentację danych poprzez zmniejszoną liczbę cech (deskryptorów) charakteryzujących dostatecznie dokładnie analizowany proces. Redukcja taka może polegać na wyborze ograniczonej liczby zmiennych oryginalnych (bez zmiany ich wartości), bądź na generacji nowego zbioru deskryptorów jako funkcji liniowej (np. PCA) bądź nieliniowej wszystkich zmiennych oryginalnych (AE).
Klasycznym rozwiązaniem tego typu jest autoencoder, poznany wcześniej. Idea uczenia autoenkodera polegała na takim doborze parametrów (wag sieci głębokiej), aby obraz wyjściowy po rekonstrukcji sygnałów skompresowanych przypominał jak najbardziej obraz oryginalny. W procesie uczenia klasycznego autoencodera porównywane były wartości sygnałów bądź piksele obrazów oryginalnego i zrekonstruowanego. Redukcja wymiarowości w takim rozwiązaniu autoencodera może być zinterpretowana jako kompresja danych, w której encoder kompresuje dane z przestrzeni oryginalnej do przestrzeni zredukowanej traktowanej zwykle jako przestrzeń ukryta (ang. latent space), natomiast decoder dokonuje dekompresji czyli rekonstrukcji danych oryginalnych.
Oczywiście, odtworzenie danych oryginalnych poprzez dekompresję charakteryzuje się pewną utratą informacji oryginalnej. Wielkość tej straty uzależniona jest od wymiaru przestrzeni skompresowanej jak również od mechanizmu uczenia sieci. Ilustracja tego typu procesu przetwarzania danych przedstawiona jest na rys. 6.29. Wektor oryginalny \( \mathbf{x} \) kodowany jest w wektor \(\mathbf{e}(\mathbf{x}) \) o zmniejszonym wymiarze, po czym dekodowany w postaci \(\mathbf{d}(\mathbf{e}(\mathbf{x})) \). Istotą klasycznego algorytmu uczenia sieci autoencodera jest taki dobór parametrów sieci, aby utrata informacji oryginalnej, czyli różnica między \(\mathbf{d}(\mathbf{e}(\mathbf{x})) \) a \( \mathbf{x} \) była jak najmniejsza. Minimalizacji podlega funkcja błędu
| \( \min E=\|\mathbf{x}-\mathbf{d}(\mathbf{e}(\mathbf{x}))\|^2 \) | (6.29) |
Zwykle w definicji dodaje się jeszcze czynniki regularyzacyjne, jak to było przedstawione w rozdziale dotyczącym klasycznego autoencodera. Klasyczny autoenkoder ma pewną wadę, wynikającą z nieciągłości danych (na przykład puste przestrzenie między klastrami). Na etapie testowania przy użyciu danych nie uczestniczących w uczeniu dekoder układu wygeneruje nierealistyczny wynik (nieprzystający do danych oryginalnych), gdyż na etapie uczenia nie „widział” danych encodera z obszaru pustego [33].

-
x
e(x)
d(e(x))
Dobrze wytrenowany autoecoder pozwala zwykle odtworzyć dane weryfikacyjne (testujące) pochodzące ze zbioru różnego od zbioru uczącego tylko z określoną dokładnością. Dochodzi przy tym drugi problem: przy niewłaściwym doborze wymiaru przestrzeni zredukowanej (zbyt duży wymiar warstwy ukrytej) może wystąpić efekt utraty zdolności generalizacyjnych (przeuczenie sieci) i odtwarzanie danych oryginalnych ze zbyt dużym błędem.
Remedium na to jest właściwa automatyczna regularyzacja sieci w procesie uczenia. Stąd powstała idea autoencodera wariacyjnego jako rozwiązania w którym proces uczenia podlega automatycznej regularyzacji w specjalny sposób zabezpieczający przed przeuczeniem i zapewniający najlepszą reprezentację danych w przestrzeni ukrytej, umożliwiającą właściwe odtworzenie (generację) procesu oryginalnego. Encoder wariacyjny stosuje kodowanie w warstwie ukrytej nie oryginalnych danych wejściowych, ale dwu wektorów: wektora wartości średnich \( \mu \) oraz wektora odchyleń standardowych \( \sigma \)
W efekcie proces uczenia składa się z następujących etapów [33]:
-
Dane wejściowe są kodowane w przestrzeni ukrytej (zredukowanej) na podstawie rozkładu statystycznego danych (ich dystrybucji). Przyjmując rozkład normalny wystarczy scharakteryzować proces poprzez wartość średnią (oczekiwaną) i macierz kowariancji (zwykle wariancji \( \sigma^2 \)).
-
Punkty z przestrzeni ukrytej (wejście dla dekodera) są próbkowane na podstawie tej dystrybucji.
-
Na podstawie tych próbek dekoder dokonuje rekonstrukcji danych w postaci wektora \( \mathbf{x} \) i oblicza błąd rekonstrukcji.
-
Błąd rekonstrukcji jest kierowany z powrotem do wejścia sieci (propagacja wsteczna) i na tej podstawie metodą gradientową dokonywana jest adaptacja parametrów sieci.
Przykładową generację danych poprzez próbkowanie przy znanym rozkładzie określonym poprzez wektor wartości średnich \( \boldsymbol{\mathbf{\mu}} \) oraz wektor standardowych odchyleń \boldsymbol{\mathbf{\sigma} } dla dekodera przedstawiono poniżej.
|
Wektor \( \boldsymbol{\mathbf{\mu} }\) |
[0.13 1.35 0.27 0.78 ...] |
|
Wektor \( \boldsymbol{\mathbf{\sigma} }\) |
[0.21 0.53 0.88 1.38 ...] |
|
Rozkład statystyczny próbek |
X1~N(0.13, 0.21), X2~N(1.35, 0.53), X3~N(0.27, 0.88), X4~N(0.78, 1.38),... |
|
Wektor po próbkowaniu |
[0.29 1.82 0.87 2.03 ...] |
Zauważmy, że generacja stochastyczna próbek według określonego rozkładu generuje różne wartości nawet przy tych samych wartościach średnich i wariancji. Wektor wartości średnich wskazuje centrum wokół którego z odchyleniem standardowym generowane są próbki. W efekcie decoder uczy się nie pojedynczych (ściśle zdefiniowanych) próbek, ale otoczenia, z którego są one próbkowane. Różnice między klasycznym i wariacyjnym rozwiązaniem autoencodera pokazane są na rys. 28.
|
Autoencoder |
\( \mathbf{x} \) |
\( \mathbf{z}=\mathbf{e}(\mathbf{x}) \) |
\( \mathbf{d}(\mathbf{z}) \) |
|
|
Autoencoder wariacyjny |
\( \mathbf{x} \) |
dystrybucja \( \mathbf{p}(\mathbf{z} | \mathbf{x}) \) |
Próbkowanie \( \mathbf{z} \sim \mathbf{p}(\mathbf{z} | \mathbf{x}) \) |
\( \mathbf{d}(\mathbf{z}) \) |
Rys. 6.28 Ilustracja różnicy między klasycznym i wariacyjnym autoencoderem
Takie rozwiązanie (przy założeniu rozkładu danych jako normalnego) sprowadza się w uczeniu VAR również do reprezentacji danych poprzez wartości średnie i macierz kowariancji, zamiast jedynie reprezentacji poszczególnych danych (pikseli obrazu). Takie rozwiązanie umożliwia regularyzację sieci w prosty sposób: zmusza encoder do zapewnienia normalności rozkładu danych w przestrzeni ukrytej. Proces realizowany przez VAR ten można więc przedstawić jak na rys. 30.
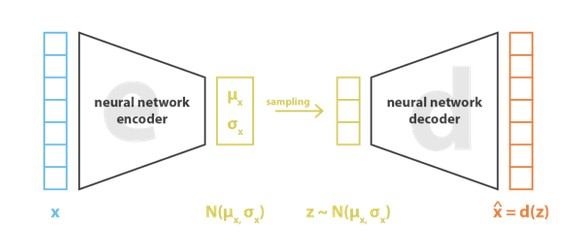
Funkcja celu podlegająca minimalizacji zawiera 2 składniki: składnik rekonstrukcyjny (dopasowanie warstwy wyjściowej do wejściowej) oraz składnik regularyzacyjny, związany z warstwą ukrytą, który dąży do zapewnienia normalności rozkładu danych w warstwie ukrytej. Składnik regularyzacyjny wyrażany jest przy użyciu dywergencji Kulbacka-Leiblera KL() między aktualnie zwracanym rozkładem danych ukrytych a pożądanym rozkładem normalnym. Minimalizowaną funkcję celu można więc zapisać w postaci
| \( \min E=\|\mathbf{x}-\mathbf{d}(\mathbf{z})\|^2+K L\left(N\left(\mu_x, \sigma_x\right), N(0,1)\right) \) | (6.30) |
Aby zapewnić prawidłowy przebieg procesu uczenia należy zapewnić regularyzację zarówno wartości średniej jak i macierzy kowariancji, sprowadzając proces do normalnego o zerowej wartości średniej i jednostkowej macierzy kowariancji. Minimalizacja wartości czynnika regularyzacyjnego odbywa się kosztem składnika rekonstrukcyjnego (składnik pierwszy we wzorze (6.30)). Właściwy balans między składnikami wzoru można uzyskać przez wprowadzenie odpowiedniej wagi w tym zbiorze.
6.9.2. Proces uczenia sieci VAR
Niech \( \mathbf{x} \) oznacza zbiór danych rekonstruowanych, generowany na podstawie ukrytych próbek z warstwy ukrytej \( \mathbf{z} \). W związku z tym wyróżnia się 2 kroki stanowiące metodę probabilistyczną uczenia
-
Próbkowanie zmiennych \( \mathbf{z} \) na podstawie rozkładu \( p(\mathbf{z}) \)
-
Próbkowanie zmiennych \( \mathbf{x} \) na podstawie rozkładu warunkowego \( p(\mathbf{x} | f(\mathbf{z})) \): znajdź rozkład zmiennej dekodowanej \( \mathbf{x} \) przy założeniu znajomości rozkładu zmiennej zakodowanej \( \mathbf{z} \).
Procesy kodowania (operator \( e \)) i dekodowania (operator \( d \)) powiązane są wzorem Bayesa
| \( p(z \mid x)=\frac{p(x \mid z) p(z)}{p(x)}=\frac{p(x \mid z) p(z)}{\sum_{u} p(x \mid u) p(u)} \) | (6.31) |
Przyjmuje się, że \( p(\mathbf{z}) \) ma standardowy rozkład Gaussa \( p(\mathbf{z}) =N(0,\mathbf{1})\), o wartości średniej zerowej i jednostkowej macierzy kowariancji \( \mathbf{1} \). Z kolei \( p(\mathbf{x} \mid \mathbf{z}) \) jest rozkładem gaussowskim, którego wartość średnia jest funkcją deterministyczną \( f(\mathbf{z}) \) zmiennej \( \mathbf{z} \) a macierz kowariancji o postaci jednostkowej pomnożonej przez dodatnią stałą wartość \( c \), co zapisuje się w postaci \( p(\mathbf{x} \mid \mathbf{z})=N(f(\mathbf{z}), c\mathbf{1}) \). Zarówno \( c \) jak i postać funkcji nie są z góry zadane i podlegają estymacji w procesie uczenia. Mianownik w wyrażeniu Bayesa wymaga zastosowania wnioskowania wariacyjnego, techniki stosowanej w złożonych rozkładach statystycznych.
W tym podejściu stosuje się sparametryzowane rodziny rozkładów (zwykle gaussowskich o różnej wartości średniej i macierzy kowariancji). Spośród nich wybiera się tę rodzinę, która minimalizuje błąd aproksymacji na danych pomiarowych (zwykle dywergencję Kulbacka-Leiblera między aproksymacją i wartościami zadanymi). Funkcja \( p(\mathbf{z} \mid \mathbf{x}) \) jest w podejściu wariacyjnym aproksymowana poprzez rozkład gaussowski
| \( q_{x}(\mathbf{z})={N}(\mathrm{g}(\mathbf{x}), \mathrm{h}(\mathbf{x})) \) | (6.32) |
w którym wartość średnia jest aproksymowana przez \( \mathrm{g}(\mathbf{x}) \) a kowariancja przez \( \mathrm{h}(\mathbf{x}) \). Obie funkcje podlegają procesowi minimalizacji z użyciem miary Kulbacka-Leiblera
| \( \left(g^*, h^*\right)=\underset{g, h}{\arg } \min K L\left(q_x(z), p(z \mid x)\right) \) | (6.33) |
Proces ten sprowadza się do rozwiązania problemu optymalizacyjnego o postaci [33]
| \( \left(g^*, h^*\right)=\underset{g, h}{\arg \max }\left(-\frac{\|x-f(z)\|^2}{2 c}-K L\left(q_x(z), p(z)\right)\right ) \) |
(6.34) |
Składnik pierwszy w tym wzorze odpowiada za dopasowanie sygnałów wyjściowych sieci do wartości zadanych \( \mathbf{x} \), natomiast składnik drugi za rozkład statystyczny danych wejściowych i sygnałów w warstwie ukrytej, stanowiąc naturalny składnik regularyzacyjny procesu. Istotnym parametrem jest \( c \). Wartość tej zmiennej pozwala regulować relację między składnikiem pierwszym i drugim. Duża wartość \( c \) oznacza większy wpływ czynnika KL, czyli dopasowania statystycznego obu rozkładów, natomiast mała wartość – większy wpływ dopasowania pikselowego zrekonstruowanego obrazu do oryginalnego.
Funkcje \( f \), \( g \) i \( h \) użyte w modelu matematycznym podlegają w praktyce modelowaniu aproksymacyjnemu przy użyciu sieci neuronowych. Obie funkcje \( g \) i \( h \) wykorzystują wspólny fragment architektury sieci, co można zapisać w postaci
| \( g(\mathbf{x})=g_2\left(g_1(\mathbf{x})\right)=g_2\left({~h}_1(\mathbf{x})\right) \) | (6.35) |
| \( h(\mathbf{x})=h_2\left(h_1(\mathbf{x})\right) \) | (6.36) |
Przyjmuje się w praktyce założenie upraszczające, że \( h(\mathbf{x}) \) jest wektorem złożonym z elementów diagonalnych macierzy kowariancji i jest jednakowych rozmiarów jak \( g(\mathbf{x}) \). Przy rozkładzie gaussowskim zmiennej \( \mathbf{z} \) o wartości średniej \( g(\mathbf{x}) \) i wariancji \( h(\mathbf{x}) \) przyjmuje się, że
| \( z=h(x) \xi+g(x) \) | (6.37) |
gdzie \( \xi \) jest zmienną losową o rozkładzie normalnym \( \xi \sim N(0,1) \). Rys. 6.31 przedstawia ogólną strukturę układową encodera implementującą funkcje \( g(\mathbf{x}) \) oraz \( h(\mathbf{x}) \), przy czym wektor \( g(\mathbf{x}) \) reprezentuje wartości średnie a \( h(\mathbf{x}) \) kowariancje (wartości diagonalne macierzy kowariancji). Rekonstrukcja sygnałów wyjściowych (decoder) realizująca rozkład \( p(\mathbf{x} \mid \mathbf{z}) \) generowany przez encoder zakłada stałą kowariancję i jest implementowana przez strukturę neuronową implementującą funkcję \( f \) o postaci na przykład z rys. 6.31 i 6.32.
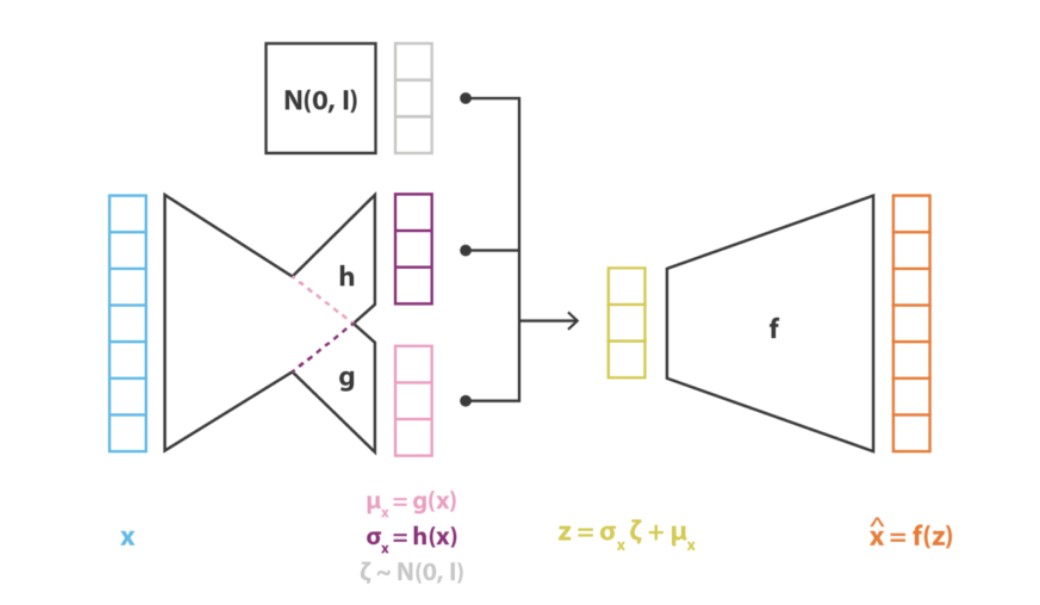
W efekcie proces uczenia sieci z rys. 6.31 sprowadza się do minimalizacji funkcji celu o postaci
| \( \min E=C\|\mathbf{x}-\mathbf{f}(\mathbf{z})\|^2+K L(N(g(x), h(x)), N(0,1)) \) | (6.38) |
Czynnik pierwszy odpowiada za odtworzenie sygnałów wejściowych na wyjściu sieci, natomiast drugi za odwzorowanie rozkładu statystycznego sygnałów wejściowych w sygnałach wyjściowych. Obie struktury (encoder i decoder) są implementowane w postaci głębokiej sieci neuronowej, podlegającej uczeniu typowemu dla sieci głębokich. Przykład takiej sieci pokazany jest na rys. 6.32.