Podręcznik

Sieć generatywna GAN (Generative Adversarial Network- GAN) stworzona przez zespół Iana Goodfellow w 2014 roku, jest implementacją koncepcji przeciwstawienia sobie dwu sieci neuronowych, z których jedna reprezentuje dane rzeczywiste, a druga dane generowane sztucznie, "udając" dane rzeczywiste [19]. Obie sieci rywalizują ze sobą. System jest trenowany w taki sposób aby generator nowych danych był w stanie oszukać rzeczywistość, prezentując dane (sygnały bądź obrazy) które są trudne do odróżnienia od rzeczywistych. Generator sztucznych danych ma za zadanie wygenerować je w taki sposób, aby statystyki danych oryginalnych i danych generowanych przez niego były takie same. Przykładowo w przypadku obrazów, obraz wygenerowany sztucznie powinien przypominać obraz oryginalny.

Idea działania sieci GAN jest przedstawiona na rys. 6.33. Blok $\mathbf{X}$ reprezentuje dane oryginalne, $\mathbf{z}$ – wektor losowy zasilający generator $G$, generujący na tej podstawie dane $G(\mathbf{z})$ „udające” dane oryginalne. Dyskryminator $D$ porównuje dane oryginalne $\mathbf{X}$ z $G(\mathbf{z})$ wygenerowanymi przez generator wskazując na prawdopodobieństwo zgodności obu danych $\mathbf{X}$ i $G(\mathbf{z})$. Proces uczenia sieci polega na takim doborze parametrów, aby oszukać dyskryminator (uznać, że dane wygenerowane sztucznie $G(\mathbf{z})$ niczym nie różnią się od danych oryginalnych $\mathbf{X}$. W efekcie generator $G$ generuje kolejnych kandydatów do porównania, a dyskryminator $D$ ocenia ich jakość w stosunku do oryginału.

Proces uczenia polega na maksymalizacji prawdopodobieństwa, że dyskryminator popełni błąd, przyjmując że obie grupy danych (oryginalne i sztucznie wygenerowane) są identyczne pod względem rozkładu statystycznego (maksymalizacja prawdopodobieństwa zaliczenia obu obrazów: oryginalnego i wygenerowanego sztucznie do tej samej klasy). Można go zapisać jako programowanie minimaksowe zdefiniowane w postaci [19]

gdzie symbol $E$ reprezentuje wartość oczekiwaną, natomiast ${p}_\mathbf{X}$ i ${p}_\mathbf{z}$ rozkłady statystyczne odpowiednio danych rzeczywistych (oryginalnych) i wygenerowanych sztucznie. $D(\mathbf{X})$ oraz $G(\mathbf{X})$  są wartościami generowanymi odpowiednio przez dyskryminator $D$ i generator $G$ dla danych $\mathbf{X}$. W efekcie proces optymalizacyjny ukierunkowany jest na poszukiwanie minimum względem generatora $G$ i maksimum względem dyskryminatora $D$.

Generator $G$ zasilany jest poprzez wektor losowy $\mathbf{z}$ o określonym wymiarze. Na bazie tego wektora próbuje wygenerować obraz przypominający oryginał $\mathbf{X}$. Dyskryminator zasilany jest przez obraz oryginalny $\mathbf{X}$ i obraz wygenerowany przez generator $G(\mathbf{z})$. W wyniku ich porównania generuje wartość prawdopodobieństwa, że obraz $G(\mathbf{z})$ jest nierozpoznawalny od oryginału $\mathbf{X}$. Oba modele $G$ i $D$ mogą być implementowane przy użyciu różnych struktur sieci neuronowych, aczkolwiek aktualnie najlepsze wyniki uzyskuje się przy użyciu sieci głębokich o strukturze CNN.

Proces uczenia sieci GAN przyjmuje formę iteracyjną. Przy aktualnych parametrach generatora $G$ wykonuje się $k$ kroków w optymalizacji dyskryminatora $D$ a następnie jeden krok optymalizacji generatora. W pętli wewnętrznej adaptacji dyskryminator jest ukierunkowany na rozróżnienie próbek obu obrazów. W kroku drugim dotyczącym adaptacji generatora jego parametry są zmieniane w takim kierunku, aby wynik generatora był bliższy obrazowi oryginalnemu. Po wykonaniu wielu iteracji osiągnięty jest punkt, w którym nie występuje możliwość poprawy wyniku w obu krokach, czyli dyskryminator nie jest w stanie rozróżnić obrazu  ${G}(\mathbf{z})$ od oryginalnego $\mathbf{X}$.

Powstało wiele modyfikacji podstawowej struktury GAN polepszających sprawność wykrywania „podróbki” od danych oryginalnych. Przykład takiego rozwiązania zwanego BIGAN (BIdirectional Generative Adversarial Networks) przedstawiony jest na rys. 6.34.

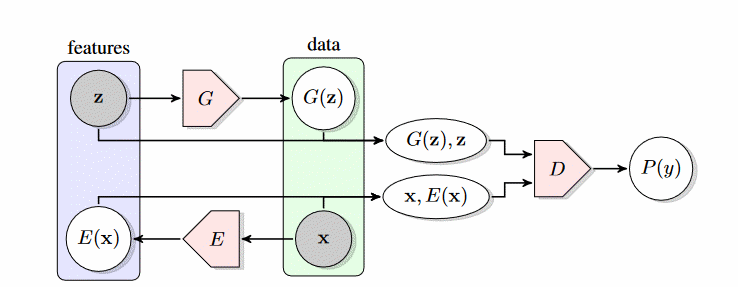
Struktura sieci BIGAN zawiera enkoder $E$ który transformuje dane oryginalne $\mathbf{X}$ do przestrzeni wektorowej $E(\mathbf{X})$, generując wektor cech o wymiarach identycznych z wektorem losowym $\mathbf{z}$. Dyskryminator $D$ sieci BIGAN dokonuje więc rozróżnienia pary danych $(\mathbf{X}, E(\mathbf{X}))$ oraz $(G(\mathbf{z}), \mathbf{z})$ zamiast ($\mathbf{X}$ versus $G(\mathbf{z})$) w klasycznej implementacji GAN. Jest oczywiste, że enkoder $E$ próbuje „nauczyć” się inwersji generatora $G$ (czyli wektora $\mathbf{z}$), choć nie występuje tu bezpośrednia komunikacja. Zwiększona informacja (w stosunku do wersji oryginalnej GAN) dostarczona do dyskryminatora umożliwia polepszenie dokładności rozpoznania „podróbki” od oryginału.

Sieci generatywne (GAN i jego różne modyfikacje) znajdują różne zastosowania. Jednym z nich jest wzbogacanie zbioru danych oryginalnych (tak zwana augmentacja zbioru) użytych w uczeniu sieci CNN. Dane wygenerowane przez GAN są podobne statystycznie do danych oryginalnych, ale nie tożsame, co jest warunkiem polepszenia zdolności generalizacyjnych trenowanych sieci. Innym zastosowaniem sieci GAN jest wykrywanie różnic między oryginałami i podróbkami. Dotyczy to zarówno obrazów jak i sygnałów. Sieci te wykazują się zwiększoną czułością w stosunku do innych rozwiązań.