2. Sieci wektorów nośnych SVM

2.4. Sieć SVM do zadań regresji

Zadaniem sieci SVM w tym zastosowaniu jest aproksymacja zbioru danych pomiarowych \( (\mathbf{x}_i, d(\mathbf{x})) \) w dziedzinie liczb rzeczywistych. W odróżnieniu od zadania klasyfikacji wielkości zadane \( d_i \) mogą przyjmować dowolne wartości rzeczywiste, a nie tylko binarne \( \pm 1 \), jak to miało miejsce w przypadku klasyfikatorów. Jest to więc zadanie bardziej złożone niż zadanie klasyfikacji. Dla uzyskania największej efektywności działania sieci i uzyskania sformułowania problemu uczenia jako programowania kwadratowego, przyjmuje się funkcję błędu z tolerancją \( \varepsilon \), definiowaną w postaci [68]


\( L_{\varepsilon}(d, y(\mathbf{x}))=\left\{\begin{array}{ccl} |d-y(\mathbf{x})|-\varepsilon & \text { dla } & |d-y(\mathbf{x})| \geq \varepsilon \\ 0 & \text { dla } & |d-y(\mathbf{x})| < \varepsilon \end{array}\right. \) (5.34)

Przyjmiemy podobnie jak w zadaniu klasyfikacji, że dane uczące \( (\mathbf{x}_i, d(\mathbf{x})) \) są aproksymowane przez funkcję


\( y(\mathbf{x})=\mathbf{w}^T \boldsymbol{\varphi}(\mathbf{x})+b \)
 (5.35)


Zadaniem uczenia jest taki dobór wektora wagowego \( \mathbf{w} \), liczby neuronów ukrytych (funkcji jąder) oraz parametrów tych funkcji, aby zminimalizować wartość funkcji błędu


\( \min E=\frac{1}{2} \sum_{i=1}^p L_{\varepsilon}\left(d_i, y\left(\mathbf{x}_i\right)\right) \)
 (5.36)

przy możliwie największym ograniczeniu wartości wag \( w_i \) sieci. Wprowadzając zmienne dopełniające \( \xi_i \), \(\xi_i^{'} \) o nieujemnych wartościach (każda odpowiedzialna za przekroczenie marginesu tolerancyjnego w górę lub w dół) zadanie pierwotne uczenia można sformułować bardziej ogólnie, analogicznie jak w zadaniu klasyfikacji jako minimalizację wartości wag sieci oraz zmiennych dopełniających \( \xi_i \), \(\xi_i^{'} \)  i zapisać w postaci [59]


\( \min \limits_{\mathbf{w}} \frac{1}{2} \mathbf{w}^T \mathbf{w}+C\left[\sum_{i=1}^p (\xi_i+\xi_i^{\prime})\right] \)
 (5.37)


przy liniowych ograniczeniach funkcyjnych zapisanych dla \( i=1,2,\ldots,p \) w postaci


\( \begin{aligned} & d_i-\left(\mathbf{w}^T \boldsymbol{\varphi}\left(\mathbf{x}_i\right)+b\right) \leq \varepsilon+\xi_i \\ & \left(\mathbf{w}^T \boldsymbol{\varphi}\left(\mathbf{x}_i\right)+b\right)-d_i \leq \varepsilon+\xi_i \\ & \xi_{\mathrm{i}} \geq 0 \\ & \xi_{\mathrm{i}}^{\prime} \geq 0 \end{aligned} \) (5.38)

Zauważmy, że dobór wartości zmiennych dopełniających \( \xi_i \), \(\xi_i^{'} \) taki, że spełniony jest warunek \( \left| d_i-\left(\mathbf{w}^T \varphi\left(\mathbf{x}_i\right)+b\right)\right| \leq\left(\varepsilon+\xi_i\right) \) zapewnia wartość \( L_{\varepsilon+\xi_i}\left(d_i, y\left(\mathbf{x}_i\right)\right)=0 \), co automatycznie minimalizuje wartość funkcji błędu \( E \) wyrażonego wzorem (5.36). W sformułowaniu zadania pierwotnego występuje stała \( C \) stanowiąca wielkość regularyzacyjną, ustalającą kompromis między wartością marginesu separacji reprezentowanego przez wagi sieci i wartością funkcji błędu aproksymacji, uzależnionego od przyjętej wartości \( \varepsilon \) oraz uzyskanych w wyniku procesu optymalizacyjnego wartości \( \xi_i \), \(\xi_i^{'} \).

Dla tak postawionego problemu pierwotnego można zdefiniować funkcję Lagrange'a, w której \( \alpha_i \) oraz \( \alpha_i ^{'}\) są mnożnikami o wartościach większych lub równych zeru w zależności od spełnienia ograniczeń funkcyjnych a \( \mu_i \) oraz \( \mu_i ^{'}\) nieujemnymi mnożnikami odpowiadającymi za ograniczenia nakładane na zmienne dopełniające \( \xi_i \), \(\xi_i^{'} \)  w zależności (5.38). Zadanie optymalizacji rozwiązuje się minimalizując funkcję Lagrange’a względem wag \( \mathbf{w} \) i zmiennych dopełniających \( \xi_i \), \(\xi_i^{'} \)  oraz maksymalizując ją względem mnożników Lagrange'a (punkt siodłowy funkcji Lagrange’a). Z rozwiązania powyższego zadania otrzymuje się sformułowanie problemu dualnego względem mnożników Lagrange'a w postaci [46,68]


\( \left.\max _{\boldsymbol{\alpha}} {Q}(\boldsymbol{\alpha})=\sum_{{i}=1}^{{p}} d_i\left(\alpha_{{i}}-\alpha_{{i}}^{\prime}\right)-\varepsilon \sum_{{i}=1}^{{p}} d_i\left(\alpha_{{i}}+\alpha_{{i}}^{\prime}\right)-\frac{1}{2} \sum_{{i}=1}^{{p}} \sum_{{j}=1}^{{p}}\left(\alpha_{{i}}-\alpha_{{i}}^{\prime}\right)\left(\alpha_{{j}}-\alpha_{{j}}^{\prime}\right)\right)K\left(\mathbf{x}_i, \mathbf{x}_j\right) \) (5.39)


przy ograniczeniach dla \( i=1,2,\ldots,p \) 


\( \begin{aligned} & 0 \leq \alpha_i \leq C \\ & 0 \leq \alpha_i^{\prime} \leq C \\ & \sum_{i=1}^p\left(\alpha_i-\alpha_i^{\prime}\right)=0 \end{aligned} \) (5.40)


W zależnościach tych \( C \) jest stałą regularyzacji dobieraną przez użytkownika a \( K\left(\mathbf{x}_i, \mathbf{x}_j\right) =\varphi^T(\mathbf{x}_i)\varphi(\mathbf{x}_j) \). Zmienne dopełniające \( \xi_i \), \(\xi_i^{'} \)  oraz towarzyszące im mnożniki Lagrange’a nie występują w sposób jawny w sformułowaniu zadania dualnego, ale są uzależnione od mnożników \( \xi_i \), \(\xi_i^{'} \)  spełniając przy tym zależności \( \mu_i=C-\alpha_i \),  \( \mu_i^{\prime}=C-\alpha_i^{\prime} \), \( \xi_i \mu_i=0 \) oraz \( \xi_i^{'} \mu_i^{'}=0 \).

Po wyznaczeniu optymalnego rozwiązania problemu dualnego względem mnożników Lagrange'a obliczane są wagi \( \mathbf{w} \) sieci na podstawie zależności


\( \mathbf{w}=\sum_{i=1}^{N_{sv}}\left(\alpha_i-\alpha_i^{\prime}\right) \boldsymbol{\varphi}\left(\mathbf{x}_i\right) \)
 (5.41)

w której \( N_{sv} \) oznacza liczbę wektorów nośnych, równą liczbie niezerowych mnożników Lagrange'a. Sygnał wyjściowy \( y(\mathbf{x}) \) sieci opisuje się zatem zależnością


\( y(\mathbf{x})=\sum_{i=1}^{N_{sv}}\left(\alpha_i-\alpha_i^{\prime}\right) K\left(\mathbf{x}, \mathbf{x}_i\right)+b \) (5.42)


Wybór wartości hiperparametrów \( C \) i \( \varepsilon \) wpływa na złożoność sieci SVM. Oba parametry powinny być ustalane przez użytkownika w procesie uczenia. Zadanie aproksymacji jest zatem problemem bardziej złożonym niż klasyfikacja.

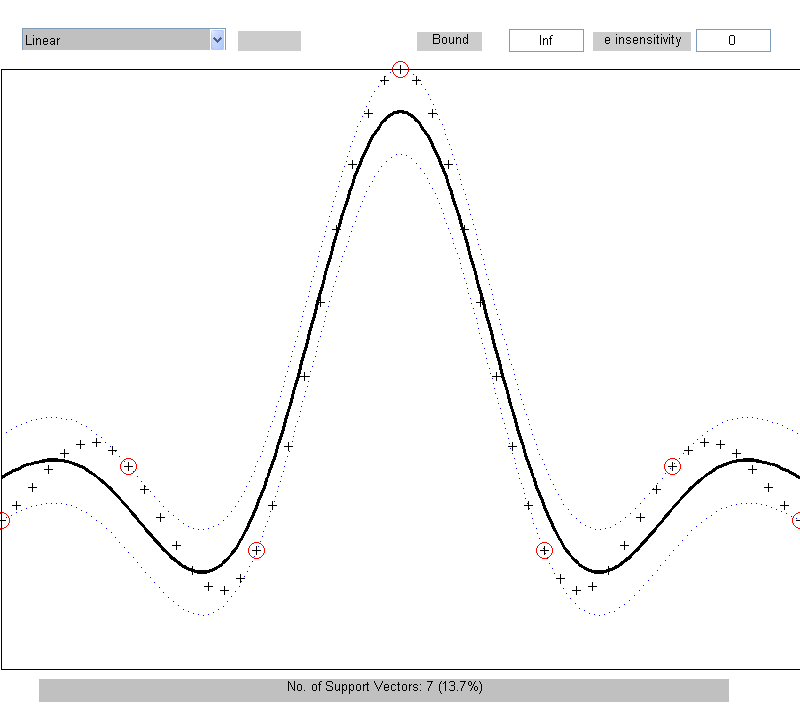
Rys. 5.7 Przykład dopasowania krzywej aproksymującej (linia ciągła) realizowanej przez sieć SVM do danych pomiarowych zaznaczonych znakiem +

Na rys. 5.7 przedstawiono wyniki działania sieci SVM w trybie regresji uzyskane przy użyciu programu Gunna [21]. Dane pomiarowe (punkty zaznaczone znakiem +) zostały aproksymowane krzywą ciągłą realizowana przez SVM. Spośród danych pomiarowych tylko nieliczne stanowią wektory podtrzymujące (punkty oznaczone znakiem + w kółku), Pozostałe punkty danych mieszczą się wewnątrz strefy zdefiniowanej przez wartość \( \varepsilon \) równą w eksperymencie \( \varepsilon = 0.1 \)  i nie wpływają na dobór parametrów sieci.