Podręcznik

Działanie programu SVM zademonstrujemy na przykładzie problemu klasyfikacji dwu spiral, uważanego za jedno z trudniejszych zadań klasyfikacyjnych. Zadaniem sieci jest klasyfikacja punktów położonych na dwu wzajemnie przeplatających się spiralach należących do dwu różnych klas. Główny problem właściwego rozpoznania klas polega na tym, że przy niewielkiej zmianie współrzędnych punktu, przynależność do klasy może zmienić się diametralnie. Na rys. 5.9 przedstawiono położenia punktów leżących na dwu spiralach i przynależnych do dwu różnych klas. W rozwiązaniu problemu zastosowano sieć SVM o dwu wejściach, odpowiadających współrzędnym punktów podlegających klasyfikacji oraz jednym neuronie wyjściowym (przynależność do jednej klasy to wartość $d=1$, natomiast do drugiej to $d=2$).

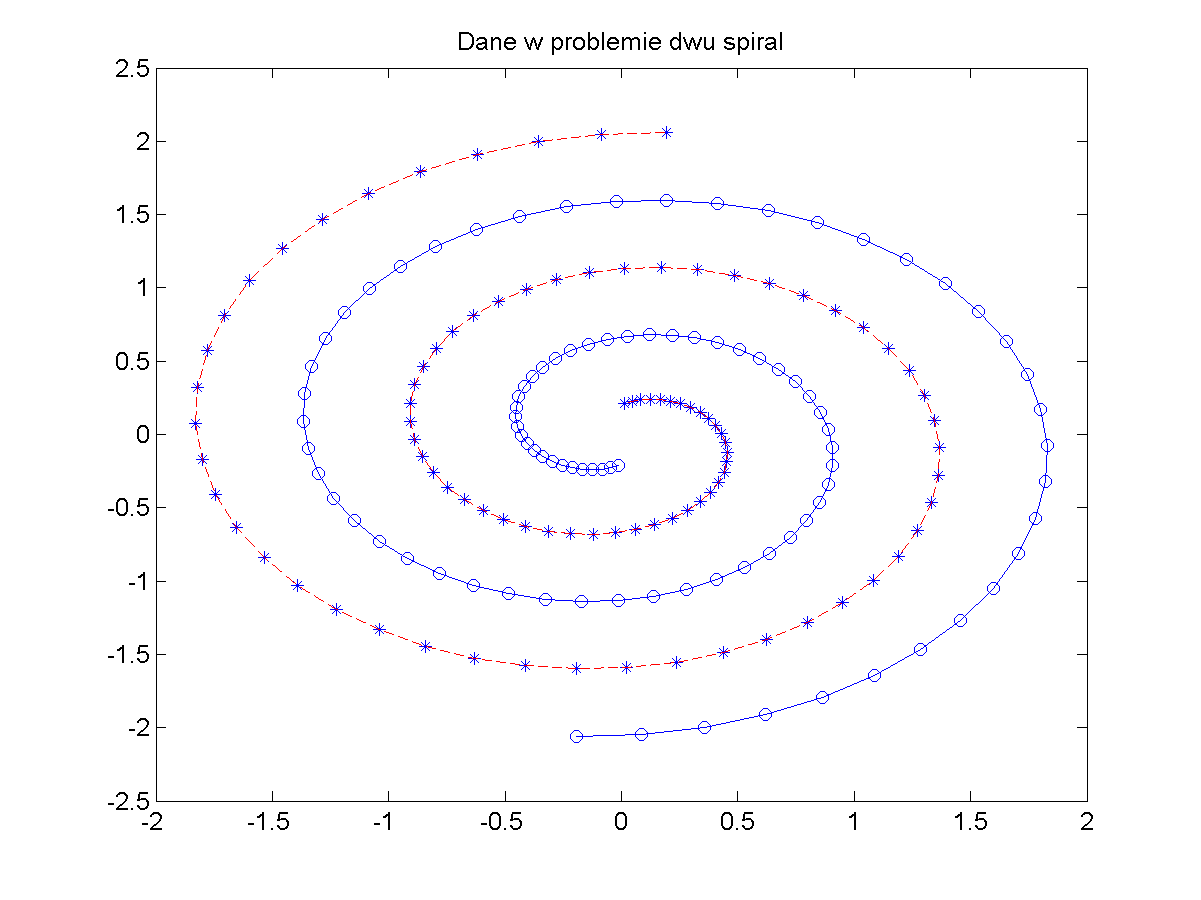
W wyniku zastosowania programu uczącego SVM otrzymano sieć zawierającą 86 wektorów podtrzymujących, która bezbłędnie klasyfikowała wszystkie dane uczące.

Tak zbudowaną sieć poddano testowaniu na danych położonych w przestrzeni kwadratowej wokół danych uczących. W wyniku skanowania tej przestrzeni uzyskano rozkład przynależności punktów do obu klas przedstawiony na rys. 5.10. Jak widać jest to gładki podział strefy wpływów obu spiral, świadczący o doskonałych własnościach generalizacyjnych sieci SVM.

5.7.2 Rozpoznawanie tekstur

Drugi przykład dotyczy rozpoznania obrazów reprezentujących 9 różnych rodzajów traw na podstawie cech teksturalnych [69]. Typowy wygląd poszczególnych rodzajów traw przedstawiony jest na rys. 5.11. Obraz z rys. 5.11a odpowiada klasie 1, rys. 5.11.b - klasie 2, rys. 5.11c - klasie 3, rys. 5.11d - klasie 4, rys. 5.11e - klasie 5, rys. 5.11f - klasie 6, rys. 5.11g - klasie 7, rys. 5.11h - klasie 8 a rys. 5.11i - klasie 9.

Obrazy tekstur zostały zaczerpnięte z bazy Vistex. Poszczególne klasy różnią się minimalnie pod względem wzrokowym i rozróżnienie między nimi należy do zadań trudnych nawet dla najbardziej skutecznych klasyfikatorów. Obrazy tekstur o wymiarach $512 \times 512$ zostały podzielone na ramki (podobrazy) o wymiarach $8 \times 8$. Każda klasa zawierała 32 dane uczące i 32 dane testujące. Tekstury były reprezentowane w eksperymencie przez zbiór 11 cech wynikających z algorytmu Markowa. Połowa ramek uczestniczyła w uczeniu, druga połowa jedynie w testowaniu. Wyniki rozpoznania tekstur użytych w testowaniu, przy zastosowaniu sieci SVM przedstawione są w tabeli 5.2.

Tabela 5.2. Wyniki rozpoznania tekstur traw

Klasyfikacja przy użyciu sieci SVM o $C=350$, o radialnej funkcji jądra przy $\gamma=1$ oraz 9 klasach wzorców została rozwiązana przy zastosowaniu strategii "jeden-przeciw-jednemu". W konkretnym przypadku przy liczbie klas $M=9$ oznaczało to konieczność wytrenowania aż 36 różnych sieci.