Podręcznik

Sieci SVM podobnie jak inne rozwiązania sieci trenowanych pod nadzorem (MLP, RBF) pełnią rolę uniwersalnego aproksymatora danych uczących. Ich główną zaletą jest dobra generalizacja, związana ze stosunkowo małą wrażliwością na liczbę danych uczących, co ma szczególne znaczenie w rozwiązaniu problemów, dla których liczba danych jest ograniczona. Pod tym względem przewyższają zdecydowanie sieci MLP, szczególnie wrażliwe na stosunek liczby danych uczących do liczby wag sieci.

Istotną zaletą sieci SVM jest możliwość płynnej regulacji jej stopnia złożoności wyrażonej miarą $VCdim$ [59] poprzez sterowanie szerokością marginesu separacji. W klasycznym algorytmie uczenia złożoność sieci (miara $VCdim$) rośnie wraz ze zwiększaniem się liczby neuronów ukrytych (z założenia liczba wejść i wyjść sieci nie podlega doborowi, gdyż zależy wyłącznie od problemu podlegającego rozwiązaniu). Jeśli liczbę neuronów ukrytych (reprezentują one cechy procesu) oznaczymy przez $K$ to w zwykłej sieci zarówno radialnej, wielomianowej jak i sigmoidalnej (w ostatnim przypadku jednowarstwowej) miara $VCdim=K+1$. Wartość $K$ może teoretycznie rosnąć nieograniczenie, zatem dla uzyskania dobrej generalizacji sieci należy odpowiednio zwiększać liczbę danych uczących. W klasycznym sposobie uczenia każdy z tych rodzajów sieci cierpi zatem na problem wielowymiarowości, narastający wraz ze zwiększaniem się wymiarów sieci. Sieci SVM stosujące specjalne sformułowanie zadania uczenia radzą sobie znacznie lepiej z tym problemem. Zostało udowodnione, że oszacowanie miary $VCdim$ dla sieci SVM spełnia następującą relację matematyczną

Funkcja entier oznacza najmniejszą liczbę całkowitą większą lub równą najmniejszej wartości zawartej wewnątrz nawiasów, $\rho$ jest wartością marginesu separacji $\rho = \frac{2}{\|w\|^2}$, $K$ - liczbą neuronów ukrytych (liczbą funkcji jądra), a $D$ - średnicą najmniejszej kuli w przestrzeni $N$-wymiarowej, obejmującej wszystkie wektory uczące $\mathbf{x}_i$ dla $i = 1, 2, \ldots, p$.

Powyższe oszacowanie potwierdza, że możliwe jest sterowanie wartością miary $VCdim$, uniezależniające ją od wymiaru $K$ przestrzeni cech. Uzyskuje się to przez właściwy dobór marginesu separacji $\rho$. Przy szerokim marginesie możliwe jest bowiem uzyskanie $\text { entier }\left(\frac{D^2}{\rho^2}\right)< K$ i wówczas oszacowanie jest niezależne od wymiaru wektora cech (liczby neuronów ukrytych). Jest to bardzo ważna zaleta sieci SVM, gdyż umożliwia świadome sterowanie stopniem złożoności sieci i w efekcie jej zdolnością generalizacji.

Dla sieci SVM użytej jako klasyfikator szacuje się często górną granicę prawdopodobieństwa $P$ wystąpienia błędu klasyfikacji na danych testujących jako stosunek liczby wektorów podtrzymujących do ogólnej liczby danych uczących, pomniejszonej o jeden

Stąd dla zwiększenia zdolności generalizacyjnych sieci dąży się do zmniejszenia liczby wektorów podtrzymujących $N_{sv}$ nawet kosztem zwiększenia liczby błędnych klasyfikacji na zbiorze danych uczących. Jakkolwiek sieci SVM stanowią rozwiązanie pozwalające kontrolować złożoność sieci i z reguły wykazując lepszą generalizację niż sieci klasyczne, ciągle brakuje dowodu matematycznego, udowadniającego ich lepsze działanie w dowolnym przypadku.

Ważną zaletą sieci SVM jest sprowadzenie problemu uczenia do zadania programowania kwadratowego, charakteryzującego się zwykle występowaniem pojedynczego minimum funkcji celu. Punkt startu w uczeniu nie ma zatem praktycznie żadnego wpływu na wynik końcowy. Zalety tej nie posiada sieć MLP, dla której funkcja celu jest nieliniowa względem optymalizowanych wag. Sieć MLP charakteryzuje się więc wieloma minimami lokalnymi. Jest zatem bardzo wrażliwa na wartości startowe parametrów optymalizowanych. Należy jednak stwierdzić, że jakość rozwiązania sieci SVM zależy w dużej mierze od przyjętych arbitralnie wartości parametrów stałych (tak zwanych "hiperparametrów") do których zaliczamy szerokość funkcji gaussowskiej $\sigma$, współczynnik $\gamma$ dla jądra wielomianowego, wartość parametru regularyzacyjnego $C$ czy tolerancję $\varepsilon$. Wartości te są dobierane zwykle metodą prób przy użyciu specjalnego zestawu danych weryfikujących, wydzielonych ze zbioru uczącego (metoda "cross validation").

Na podstawie wielu eksperymentów numerycznych przeprowadzonych zarówno na danych syntetycznych typu "benchmark" jak i problemów rzeczywistych można stwierdzić, że sieci SVM są bezkonkurencyjne w stosunku do innych rozwiązań sieci klasycznych w zdecydowanej większości zadań klasyfikacji. W przypadku zadań regresji przewaga sieci SVM nad MLP nie jest już tak oczywista. Zwykle wyniki są tu porównywalne i sieć MLP może stanowić dobrą alternatywę dla SVM.

Interesujące jest porównanie sieci SVM i RBF (obu stosujących funkcje gaussowską neuronów ukrytych) na dobór struktury sieci. Pokażemy to na przykładzie zadania regresji polegającej na kalibracji danych "sztucznego nosa" [5].

Układ pięciu czujników półprzewodnikowych poddano działaniu mieszaniny 4 gazów (tlenku węgla, metanu, propan-butanu i metanolu). Charakterystyki czujników są wysoce nieselektywne i określenie na podstawie ich wskazań stężenia poszczególnych składników wymaga procesu kalibracji, czyli stowarzyszenia poszczególnych stężeń ze wskazaniami czujników. Rolę tę może pełnić dowolna sieć neuronowa trenowana z nauczycielem. W tym eksperymencie pokażemy wyniki dla sieci SVM i RBF. Obie sieci można bez trudu wytrenować w taki sposób, że wskazania sieci będą z błędem mniejszym niż 1% pokrywać się z wartościami idealnymi dla danych testujących. Istotny jest przy tym dobór parametrów uczących stałych: wartości $\sigma$ dla sieci RBF i $\gamma$ dla sieci regresyjnej SVM. Te dwa parametry są decydujące o złożoności sieci (liczbie neuronów ukrytych). Zmieniając je można zbadać jak zmienia się zdolność generalizacji sieci przy różnej liczbie neuronów ukrytych. Na rys. 5.12 przedstawiono błędy uczenia i testowania dla obu sieci w funkcji liczby neuronów ukrytych (zależnych od wartości $\gamma$ w sieci RBF przy użyciu algorytmu Grama-Schmidta i parametru  $\varepsilon$ dla sieci SVM trenowanej przy pomocy algorytmu BSVM).

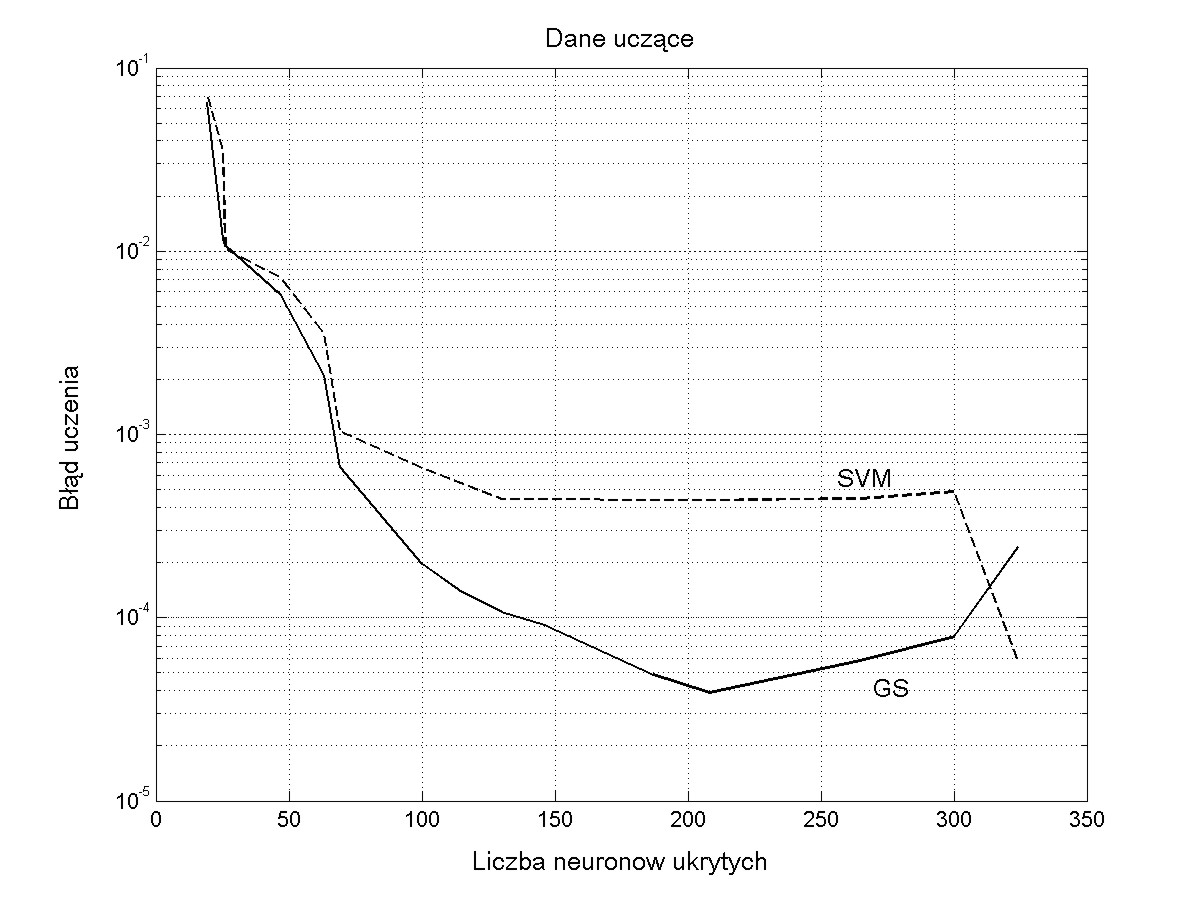
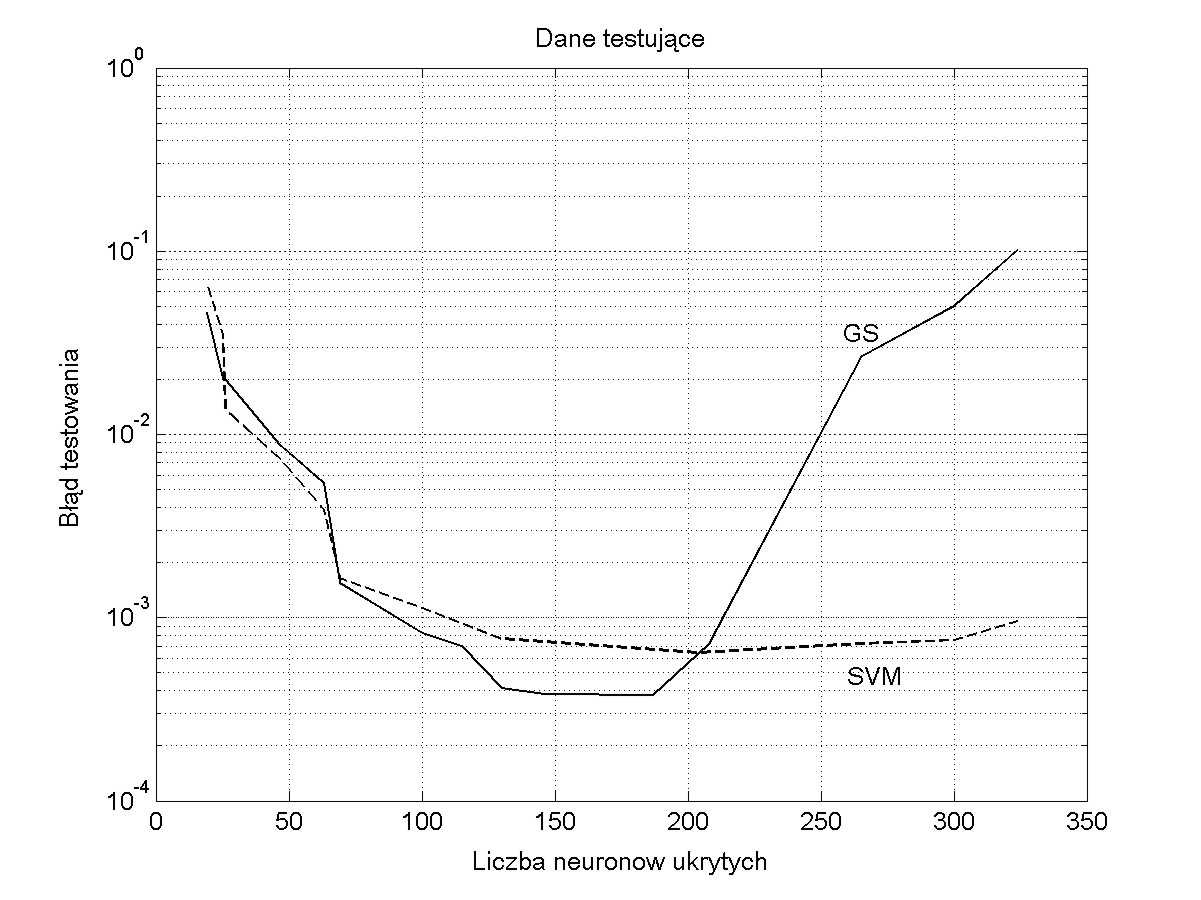
Widoczna jest przewaga sieci SVM pod względem zdolności generalizacyjnych (wyniki na danych testujących z rys. 5.12b) . Sieć ta tylko w niewielkim stopniu jest wrażliwa na dobrane przez użytkownika hiperparametry uczenia i wynikającą stąd liczbę neuronów ukrytych. Tak dobre wyniki otrzymuje się dzięki członowi regularyzacyjnemu związanemu z wartością stałej $C$. Zalety tej nie ma sieć RBF, dla której po przekroczeniu optymalnej liczby neuronów ukrytych błąd testowania gwałtownie rośnie.