Podręcznik: Sieć Elmana

4. Sieci rekurencyjne

4.1. Sieć Elmana

10.1.1 Struktura sieci Elmana

Sieć rekurencyjna Elmana charakteryzuje się częściową rekurencją w postaci sprzężenia zwrotnego między warstwą ukrytą a warstwą wejściową [24,46], realizowaną za pośrednictwem jednostkowych opóźnień oznaczanych poprzez blok opisany funkcją $z^{-1}$ . Pełną strukturę tej sieci przedstawiono na rys. 10.1.

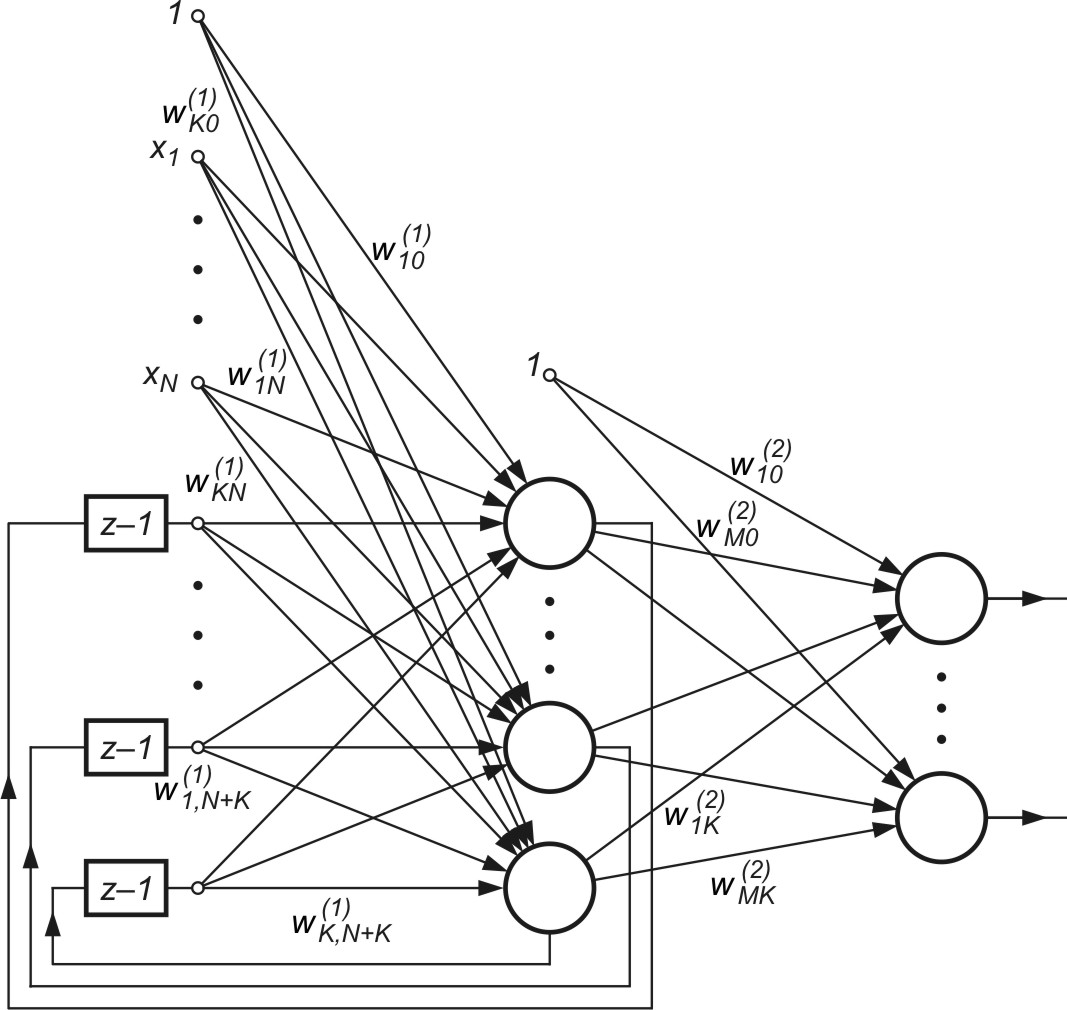
Rys. 10.1 Struktura układowa sieci rekurencyjnej Elmana

Każdy neuron ukryty ma swój odpowiednik w tak zwanej warstwie kontekstowej, stanowiącej wspólnie z wejściami zewnętrznymi sieci rozszerzoną warstwę wejściową. Warstwę wyjściową tworzą neurony połączone jednokierunkowo tylko z neuronami warstwy ukrytej, tak jak w przypadku sieci MLP. Oznaczmy zewnętrzny wektor wymuszający sieci przez $\mathbf{x}$ (do jego składu należy także sygnał jednostkowy polaryzacji $x_0=1$ , stany neuronów ukrytych przez $\mathbf{v}$ , a sygnały wyjściowe sieci przez $\mathbf{y}$ . Załóżmy, że wymuszenie $\mathbf{x}$ w chwili $k$ podane na sieć generuje w warstwie ukrytej sygnały $v_i(k)$ a w warstwie wyjściowej sygnały $y_i(k)$ odpowiadające danej chwili. Biorąc pod uwagę bloki opóźniające w warstwie kontekstowej pełny wektor wejściowy sieci w chwili $k$ przyjmie postać $\mathbf{x}(k)=\left[x_0(k), x_1(k), \ldots, x_N(k), v_1(k-1),v_2(k-1), \ldots v_K(k-1) \right]$ . Wagi połączeń synaptycznych warstwy pierwszej (ukrytej) oznaczymy przez $w_{ij}^{(1)}$ , warstwy drugiej (wyjściowej) przez ${w}_{ij}^{(2)}$ . Przy oznaczeniu sumy wagowej $i$ -tego neuronu warstwy ukrytej przez $u_i$ , a jego sygnału wyjściowego przez $v_i$ , otrzymuje się

$u_i(k)=\sum_{j=0}^{N+K} w_{i j}^{(1)} x_j(k)$

(10.1)

$v_i(k)=f_1\left(u_i(k)\right)$

(10.2)

Wagi $w_{ij}^{(1)}$ tworzą macierz $\mathbf{W}^{(1)}$ połączeń synaptycznych w warstwie ukrytej, a $f_1(u_i)$ jest funkcją aktywacji $i$ -tego neuronu tej warstwy. Podobnie można oznaczyć przez $g_i$ sumę wagową $i$ -tego neuronu warstwy wyjściowej, a przez $y_i$ odpowiadający mu $i$ -ty sygnał wyjściowy sieci. Sygnały te są opisane wzorami

$g_i(k)=\sum_{j=0}^K w_{i j}^{(2)} v_j(k)$

(10.3)

$y_i(k)=f_2\left(g_i(k)\right)$

(10.4)

Wagi $w_{ij}^{(2)}$ tworzą z kolei macierz $\mathbf{W}^{(2)}$ opisującą wagi połączeń synaptycznych neuronów warstwy wyjściowej, a $f_2(g_i)$ jest funkcją aktywacji $i$ -tego neuronu tej warstwy.

10.1.2 Algorytmy uczenia sieci Elmana

W uczeniu sieci Elmana, podobnie jak w sieciach MLP, zastosowana będzie metoda gradientowa, wywodzącą się z prac R. Williamsa i D. Zipsera [24,46]. W odróżnieniu od sieci MLP podstawą uczenia jest tu minimalizacja funkcji celu dla każdej chwili czasowej (proces jest rekurencyjny i optymalizacja dotyczyć będzie wielu chwil czasowych aż do ustabilizowania się procesu) Stąd istotnym problemem jest określenie wzorów umożliwiających proste i szybkie obliczenie gradientu funkcji celu. Funkcję celu w chwili $k$ definiować będziemy jako sumę kwadratów różnic między aktualnymi wartościami sygnałów wyjściowych sieci a ich wielkościami zadanymi dla wszystkich M neuronów wyjściowych. Przy założeniu jednej pary uczącej funkcję celu określa wzór

$E(k)=\frac{1}{2} \sum_{i=1}^M\left[y_i(k)-d_i(k)\right]^2=\frac{1}{2} \sum_{i=1}^M e_i(k)^2$

(10.5)

gdzie $e_i(k)=y_i(k)-d_i(k)$ oznacza błąd dopasowania i-tego neuronu do wartości zadanej w chwili k. Przy wielu danych uczących funkcja celu jest sumą tych zależności dla każdej pary danych. Dla określenia gradientu należy zróżniczkować funkcję celu względem wszystkich adaptowanych wag sieci. W przypadku wag występujących w warstwie wyjściowej, otrzymuje się

$g_{\alpha \beta}^{(2)}=\frac{\partial E(k)}{\partial w_{\alpha \beta}^{(2)}}=\sum_{i=1}^M e_i(k) \frac{d f_2\left(g_i(k)\right)}{d g_i(k)} \frac{d g_i(k)}{d w_{\alpha \beta}^{(2)}}$

(10.6)

Po uwzględnieniu wzoru (10.3) i (10.4) zależność (10.6) można przedstawić w postaci

$g_{\alpha \beta}^{(2)}=\sum_{i=1}^M e_i(k) \frac{d f_2\left(g_i(k)\right)}{d g_i(k)} \sum_{j=0}^K \frac{d\left(w_{i j}^{(2)} v_j(k)\right)}{d w_{\alpha \beta}^{(2)}}=\sum_{i=1}^M e_i(k) \frac{d f_2\left(g_i(k)\right)}{d g_i(k)} \sum_{j=0}^K\left(\frac{d v_j}{d w_{\alpha \beta}^{(2)}} w_{i j}^{(2)}+\frac{d w_{i j}^{(2)}}{d w_{\alpha \beta}^{(2)}} v_j(k)\right)$

(10.7)

Połączenia między warstwą ukrytą a wyjściową są jednokierunkowe (patrz rys. 10.1), stąd $\frac{d v_j}{d w_{\alpha \beta}^{(2)}}=0$ . Uwzględniając powyższy warunek otrzymuje się ostatecznie dla chwili $k$

$g_{\alpha \beta}^{(2)}(k)=\sum_{i=1}^M e_i(k) \frac{d f_2\left(g_i(k)\right)}{d g_i(k)} \sum_{j=0}^K \frac{d w_{i j}^{(2)}}{d w_{\alpha \beta}^{(2)}} v_j(k)=e_\alpha(k) \frac{d f_2\left(g_\alpha(k)\right)}{d g_\alpha(k)} v_\beta(k)$

(10.8)

Po wygenerowaniu gradientu adaptacja wag warstwy wyjściowej może odbywać się podobnie jak w sieci MLP, przy zastosowaniu metody gradientowej. W przypadku wagi $w_{\alpha \beta}^{(2)}$ zależność ta przyjmuje postać

$w_{\alpha \beta}^{(2)}(k+1)=w_{\alpha \beta}^{(2)}(k)+\eta p_{\alpha \beta}^{(2)}(k)$

(10.9)

w której $p_{\alpha \beta}^{(2)}(k)$ oznacza kierunek zmian wartości wag $w_{\alpha \beta}^{(2)}$ przyjęty w kolejnej iteracji. Wyznaczenie wektora kierunkowego $\mathbf{p}$ (w szczególności jego składowej $p_{\alpha \beta}^{(2)}$ ) odbywać się może przy użyciu różnych metod, na przykład Levenberga-Marquardta, zmiennej metryki, gradientów sprzężonych czy największego spadku [14].

Przykładowo przy zastosowaniu metody największego spadku kierunek ten wynika bezpośrednio w odpowiedniej składowej gradientu $p_{\alpha \beta}^{(2)}(k)=-g_{\alpha \beta}^{(2)}(k)$ . Proste porównanie z siecią perceptronową wskazuje, że wagi warstwy wyjściowej sieci Elmana poddane są identycznej adaptacji jak wagi neuronów wyjściowych perceptronu wielowarstwowego.

Wzory adaptacji wag warstwy ukrytej w sieci Elmana są bardziej złożone z powodu istnienia sprzężeń zwrotnych między warstwą ukrytą a warstwą wejściową (kontekstową). Obliczenie składowych wektora gradientu funkcji celu względem wag warstwy ukrytej wymaga wykonania znacznie więcej operacji matematycznych i pamiętania ostatnich wartości gradientu. Składowa gradientu funkcji celu względem wagi $w_{\alpha \beta}^{(1)}$ określona jest wzorem

$g_{\alpha \beta}^{(1)}=\frac{\partial E(k)}{\partial w_{\alpha \beta}^{(1)}}=\sum_{i=1}^M e_i(k) \frac{d f_2\left(g_i(k)\right)}{d g_i(k)} \sum_{j=1}^K \frac{d\left(v_j(k) w_{i j}^{(2)}\right)}{d w_{\alpha \beta}^{(1)}}=\sum_{i=1}^M e_i(k) \frac{d f_2\left(g_i(k)\right)}{d g_i(k)} \sum_{j=1}^K \frac{d\left(v_j(k)\right)}{d w_{\alpha \beta}^{(1)}} w_{i j}^{(2)}$

(10.10)

Po uwzględnieniu zależności (10.2) otrzymuje się

$\frac{d v_j(k)}{d w_{\alpha \beta}^{(1)}}=\frac{d f_1\left(u_j\right)}{d u_j} \sum_{m=0}^{N+K} \frac{d\left(x_m(k) w_{j m}^{(1)}\right)}{d w_{\alpha \beta}^{(1)}}=\frac{d f_1\left(u_j\right)}{d u_j}\left[\delta_{j \alpha} x_\beta+\sum_{m=0}^{N+K} \frac{d x_m(k)}{d w_{\alpha \beta}^{(1)}} w_{j m}^{(1)}\right]$

(10.11)

Gdzie $\delta_{j \alpha}$ oznacza symbol Kroneckera. Uwzględniając definicję wektora wejściowego $\mathbf{x}$ dla chwili $k$ uzyskuje się

$\frac{d v_j(k)}{d w_{\alpha \beta}^{(1)}}=\frac{d f_1\left(u_j\right)}{d u_j}\left[\delta_{j \alpha} x_\beta+\sum_{m=N+1}^{N+K} \frac{d v_{m-N}(k-1)}{d w_{\alpha \beta}^{(1)}} w_{j m}^{(1)}\right]=\frac{d f_1\left(u_j\right)}{d u_j}\left[\delta_{j \alpha} x_\beta+\sum_{m=1}^K \frac{d v_m(k-1)}{d w_{\alpha \beta}^{(1)}} w_{j, m+N}^{(1)}\right]$

(10.12)

Podstawienie tej zależności do wzoru (10.10) umożliwia obliczenie pochodnych funkcji celu względem wag warstwy ukrytej dla każdej chwili $k$ . Należy zauważyć, że jest to wzór rekurencyjny, określający pochodną w chwili $k$ w uzależnieniu od jej wartości w chwili poprzedzającej $(k-1)$ . Wartości startowe wszystkich pochodnych dla chwili początkowej $k=0$ przyjmuje się zwykle zerowe. Podsumowując, algorytm uczenia sieci Elmana można przedstawić w następującej postaci:

Uczenie rozpocząć od przypisania wszystkim wagom losowych wartości wstępnych. Zwykle przyjmuje się rozkład równomierny, zawierający się w pewnym przedziale wartości, np. $(-1, 1)$ .
Dla kolejnych chwil czasowych $k ;\ (k = 0, 1, 2,\ldots)$ określić stan wszystkich neuronów w sieci (sygnały $v_i$ oraz $y_i$ w odpowiedzi na pobudzenia wchodzące w skład par uczących. Na tej podstawie wyznaczyć wektor wejściowy $\mathbf{x}(k)$ dla kolejnej chwili $k$ (aż do ustabilizowania się odpowiedzi sieci) dla każdej pary danych uczących.
Określić wektor błędów dopasowania $\mathbf{e}(k)$ dla neuronów warstwy wyjściowej w postaci różnic między aktualnymi i zadanymi wartościami sygnałów neuronów wyjściowych.
Wyznaczyć wektor gradientu funkcji celu względem wag warstwy wyjściowej i ukrytej, korzystając ze wzorów (10.8) i (10.10).
Dokonać uaktualniania wag sieci według zależności (10.9) wynikającej z przyjętej metody wyznaczania kierunku
1. dla neuronów warstwy wyjściowej sieci

$w_{\alpha \beta}^{(2)}(k+1)=w_{\alpha \beta}^{(2)}(k)+\eta p_{\alpha \beta}^{(2)}(k)$

(10.13)

dla neuronów warstwy ukrytej sieci

$w_{\alpha \beta}^{(1)}(k+1)=w_{\alpha \beta}^{(1)}(k)+\eta p_{\alpha \beta}^{(1)}(k)$

(10.14)

Po uaktualnieniu wartości wag następuje powrót do punktu 2 algorytmu dla kolejnej chwili $k$ aż do ustabilizowania się wartości wag.

W celu uproszczenia oznaczeń przy wyprowadzaniu wzorów adaptacji sieci założono istnienie jednej pary uczącej (wersja algorytmu on-line), w której adaptacja wag następowała po prezentacji każdej pary uczącej $(\mathbf{x}, \mathbf{d})$ . Zwykle znacznie skuteczniejszy jest algorytm off-line, w którym adaptacja wag zachodzi dopiero po prezentacji wszystkich par uczących. Realizacja takiej wersji algorytmu jest analogiczna do przedstawionej uprzednio, z tą różnicą, że należy zsumować składowe gradientu od kolejnych par uczących, a proces zmiany wag przeprowadzić każdorazowo dla pełnego zbioru danych uczących.

Omówiony algorytm należy do grupy algorytmów nielokalnych, w których adaptacja jednej wagi wymaga znajomości wartości wszystkich pozostałych wag sieci oraz sygnałów poszczególnych neuronów. Jego wymagania co do pamięci komputera są dodatkowo zwiększone potrzebą przechowywania wszystkich wartości pochodnych $\frac{d v_j(k)}{d w_{\alpha \beta}^{(1)}}$ odpowiadających poprzednim chwilom czasowym. Pomimo tego sieć rekurencyjna może być konkurencyjna w stosunku do sieci jednokierunkowej MLP, gdyż jej złożona struktura układowa jest w stanie zaadaptować się do wymagań uczących przy znacznie mniejszej liczbie neuronów ukrytych (mniejsza złożoność sieci), pozwalając uzyskać lepsze zdolności generalizacji.

10.1.3 Program uczący sieci Elmana

Przy projektowaniu programu uczącego sieci Elmana wykorzystano toolbox "Neural Network" i inne funkcje wbudowane w programie Matlab [46,43]. Pakiet programów nosi nazwę ELMAN.m (nazwa pliku uruchomieniowego). Uruchomienie programu następuje w oknie komend Matlaba po napisaniu nazwy Elman. Pojawi się wówczas menu główne przedstawione na rys. 10.2.

Rys. 10.2 Okno menu głównego programu ELMAN

W lewej części menu znajdują się: pole do zadawania danych uczących (pole Dane uczące), oraz testujących, nie uczestniczących w uczeniu (pole Dane testujące). Wczytywanie danych może odbywać się z jednego pliku z rozszerzeniem .mat grupującego wszystkie 4 grupy danych (macierz zawierająca wektory uczące $\mathbf{x}_u$ , macierz zawierająca uczące wektory zadane $\mathbf{d}_u$ , macierz zawierająca wektory testujące $\mathbf{x}_t$ , macierz zawierająca testujące wektory zadane $\mathbf{d}_t$ . Można również wczytać uprzednio zapamiętaną sieć (przycisk Wczytaj sieć).

Definiowanie struktury sieciowej odbywa się w polu środkowym menu (pole Struktura sieci). Można wybrać liczbę neuronów w warstwie ukrytej (sieć zawiera tylko jedną warstwę ukrytą) jak również rodzaj funkcji aktywacji neuronów. Dostępne są następujące funkcje: liniowa (Lin), sigmoidalna jedno polarna (Sigm) oraz sigmoidalna bipolarna (Bip). Liczba węzłów wejściowych oraz neuronów wyjściowych są automatycznie wyznaczane na podstawie wymiaru wektorów $\mathbf{x}$ oraz $\mathbf{d}$ i użytkownik nie może ich zmienić.

W praktycznej implementacji algorytmu uczenia sieci Elmana zastosowano metodę adaptacji wag typu off-line, wykorzystując te same algorytmy uczenia co dla sieci MLP. Różnią je metody określania gradientu (w sieci Elmana istnieje konieczność pamiętania wektora gradientu z poprzednich cykli uczących). Przy zastosowaniu w programie adaptacyjnego współczynnika uczenia ? dopasowującego się do aktualnych zmian wartości funkcji celu w procesie uczenia uzyskuje się sprawne narzędzie, które pozwala na skuteczne przeprowadzenie uczenia sieci odwzorowującej złożone procesy dynamiczne.

10.1.4 Przykładowe zastosowania sieci Elmana w prognozowaniu zapotrzebowania na energię elektryczną

Sieć Elmana jest siecią rekurencyjną o sprzężeniu zwrotnym z warstwy ukrytej do warstwy wejściowej. Ze względu na bezpośredni wpływ sygnałów z chwili (n-1) na stan wymuszenia w n-tej chwili, sieć taka ma naturalną predyspozycję do modelowania ciągów czasowych. Oznacza to, że sieć tego rodzaju może znaleźć zastosowanie w prognozowaniu. Tutaj przedstawimy zastosowanie sieci Elmana do prognozowania profilu 24-godzinnego zapotrzebowania na energię elektryczną w Polskim Systemie Elektroenergetycznym (PSE) z wyprzedzeniem jednodniowym.

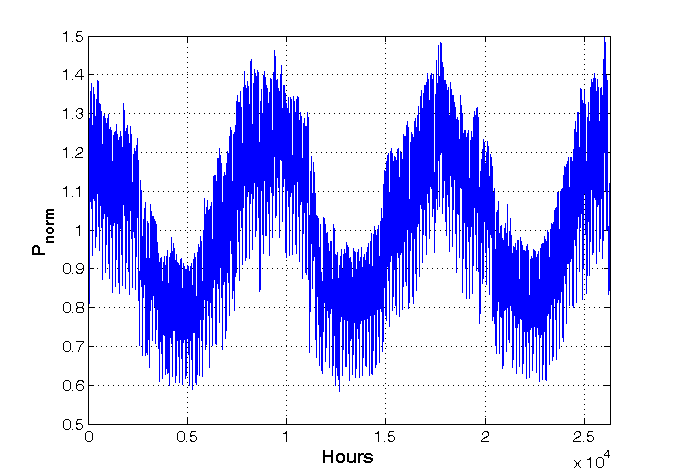
Problem predykcji wektora 24-elementowego należy do zadań trudnych ze względu na duże zmiany obciążeń godzinnych nawet w obrębie sąsiednich dni i godzin. Na rys. 10.3 przedstawiono typowy rozkład obciążeń względnych (odniesionych do wartości średniej) w PSE w przeciągu ostatnich 3 lat. Widoczne są znaczne zmiany obciążeń od wartości 0,6 do 1.4 (w wartościach względnych). Przy średnim obciążeniu rzeczywistym na poziomie $P_m=16019MW$ odchylenie standardowe było równe $\sigma=2800MW$ . Tak duży stosunek odchylenia standardowego do wartości średniej jest miara skali trudności w prognozie.

Rys. 10. 3 Rozkład godzinny obciążeń względnych w PSE w przeciągu 3 lat

W prognozie wartości względnych obciążeń zastosowano sieć Elmana. Wielkościami wejściowymi (zewnętrznymi) dla sieci prognozującej były

Znormalizowane obciążenia ostatnich 4 godzin tego samego dnia oraz 5 godzin z 3 ostatnich dni (4 godziny wstecz i godzina aktualnej prognozy) - w sumie 19 składowych
Kod pory roku: 00 – wiosna, 01 - lato, 10 – jesień, 11 – zima – w sumie 2 składowe
Kod typu dnia: 11 – dni robocze, 10 – soboty, 01 – piątki, 00 –niedziele i święta - w sumie 2 składowe

Wektor wejściowy zewnętrzny zawierał więc 23 składowe. Neurony w warstwie ukrytej były sigmoidalne, a ich liczba ustalona w wyniku eksperymentów wstępnych równa 8. Liczba neuronów w warstwie wyjściowej była równa liczbie godzin dla których dokonywano prognozy (24). Funkcja aktywacji tych neuronów była liniowa. Strukturę sieci zastosowanej w prognozie można więc zapisać w postaci 23-8-24.

Sieć poddano uczeniu na danych odpowiadających obciążeniom z 2 lat. Po nauczeniu parametry sieci zostały zamrożone i sieć poddano testowaniu na danych z jednego roku (365 dni odpowiadających 8760 godzinom). Wyniki testów zostały porównane ze znanymi wartościami rzeczywistymi dla tych samych godzin. W wyniku porównania określono następujące rodzaje błędów:

średni błąd procentowy (MAPE)

$M A P E=\frac{1}{n} \sum_{h=1}^n \frac{|P(h)-\widehat{P}(h)|}{|P(h)|} \cdot 100 \%$

(10.15)

gdzie $n$ oznacza liczbę godzin biorących udział w prognozie (u nas 8760 godzin), $P(h)$ – obciążenie rzeczywiste w godzinie $h$ , a $\widehat{P}(h)$ obciążenie prognozowane na tę godzinę.

błąd średniokwadratowy (MSE)

$M S E=\frac{1}{n} \sum_{h=1}^n[P(h)-\widehat{P}(h)]^2$

(10.16)

znormalizowany błąd średniokwadratowy (NMSE)

$NMSE=\frac{MSE}{[\operatorname{mean}(P)]^2}$

(10.17)

gdzie $\operatorname{mean}(P)$ oznacza wartość średnią obciążenia występującą w okresie prognozy.

maksymalny błąd procentowy (MAXPE)

$MAXPE=\max \left\{\frac{|P(h)-\widehat{P}(h)|}{|P(h)|} \cdot 100 \%\right\}$

(10.18)

Tabela 10.1 przedstawia uzyskane wyniki prognozy profilu 24-godzinnego obciążeń w PSE dla jednego roku w postaci błędów średnich. Dane poddane prognozie nie uczestniczyły w uczeniu

Tabela 10.1 Wyniki prognozy profilu 24-godzinnego obciążenia w PSE w postaci różnych rodzajów błędów dla sieci Elmana

MAPE [%]	MAXPE [%]	MSE [MW²]	NMSE
2.26	24.95	3.14e5	1.22e-3

Dla porównania wzrokowego jakości systemu prognozy na rys. 10.4 przedstawiono nałożone na siebie wartości prognozowane oraz rzeczywiste obciążeń godzinnych dla jednego wybranego tygodnia. Jak widać prognoza dobrze śledzi wartości rzeczywiste.

Rys. 10.4 Przykładowy rozkład prognozowanych i rzeczywistych obciążeń godzinnych dla PSE dla wybranego tygodnia w roku uzyskany przy zastosowaniu sieci Elmana (niebieski – wartości rzeczywiste, czerwony – prognoza)