Podręcznik
4. Sieci rekurencyjne
4.2. Sieć głęboka LSTM
10.2.1 Wprowadzenie
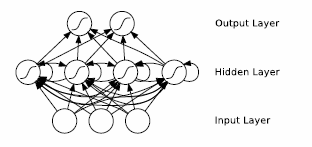
Sieci rekurencyjne LSTM dopuszczają sprzężenia zwrotne między neuronami jedynie w warstwie ukrytej. Typowy przykład takiej struktury zawierającej sprzężenia zwrotne jedynie między neuronami ukrytymi w warstwie przedstawiono na rys. 10.5 [58].
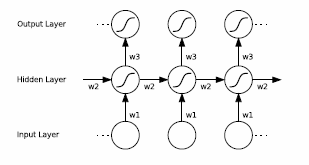
Sygnał wyjściowy neuronu zależy nie tylko od pobudzenia w danej chwili, ale również od stanu neuronów w chwili poprzedniej. Można to przedstawić w postaci rozłożonej w czasie jak na rys. 10.6 [19], w której sprzężenie zostało zamienione na przepływ jednokierunkowy sygnałów z uwzględnieniem kolejnych chwil czasowych. Stan neuronów w kolejnych chwilach: \(t, t+1, t+2\) aż do końca okna pomiarowego \(T\) zależy również od ich stanu w chwilach wcześniejszych. Układ taki można więc traktować jako sieć głęboką.
|
|
\( t \qquad t+1 \qquad t+2 \qquad t \rightarrow T \) |
|
Warstwa wyjściowa Warstwa ukryta Warstwa wejściowa |
|
W uczeniu takiej sieci występuje problem tak zwanego zanikającego gradientu. W kolejnych chwilach czasowych zależność funkcji gradientu od sygnału wejściowego sprzed poprzednich chwil czasowych powoli zanika, co powoduje utratę pewnej ilości informacji pierwotnie dostarczonej do sieci. Ten efekt może być zilustrowany jak na rys. 10.7. Stopień zaczernienia węzłów ilustruje wpływ sygnału wejściowego z chwili \(t=1\) na stan neuronów w chwilach późniejszych (im bardziej ciemny kolor tym większy wpływ). Klasyczne rozwiązanie sieci rekurencyjnej nie gwarantuje więc dobrego zapamiętania wcześniej wytrenowanych wzorców. Oznacza to utratę informacji, która była wprowadzona we wcześniejszych etapach uczenia sieci.
Skuteczne rozwiązanie tego problemu było możliwe dzięki wprowadzeniu specjalizowanej struktury rekurencyjnej, zwanej siecią Long Short-Term Memory (w skrócie LSTM) [58].
| Warstwa wyjściowa |
 |
| Warstwa ukryta | |
| Sygnały wejściowe |
10.2.2 Zasada działania sieci LSTM
Sieć ta należy do sieci rekurencyjnych o strukturze specjalnie dostosowanej do długiego zapamiętywania krótkich wzorców (short term). Składa się z wielu rekurencyjnie połączonych bloków zwanych blokami pamięciowymi [58]. Każdy taki blok zawiera trzy bramki multiplikatywne: wejściową, wyjściową oraz pamięci, pełniące rolę sterowanych zaworów. Typowa struktura komórki bloku pamięciowego używanej w LSTM przedstawiona jest na rys. 10.8.
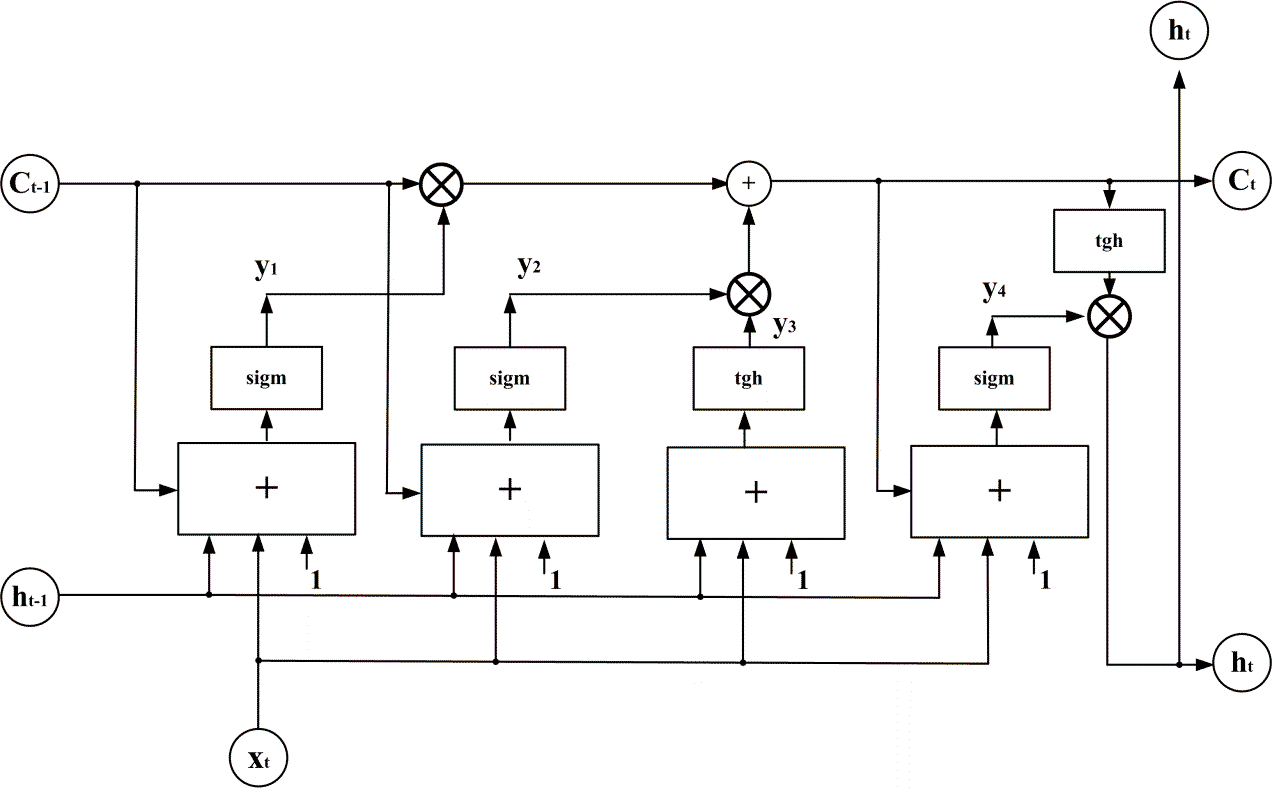
Komórka pamięciowa zawiera trzy wejścia. Są to
Xt – sygnał wejściowy w aktualnej chwili czasowej t
Ct-1 – sygnał pamięci z chwili t-1 poprzedniej komórki pamięci
ht-1 – sygnał wyjściowy z chwili t-1 poprzedniej komórki pamięci
Jednocześnie komórka ta wytwarza dwa rodzaje sygnałów wyjściowych istotnych z punktu widzenia współdziałania komórek ze sobą. Są to
Ct – sygnał pamięci w aktualnej chwili czasowej t danej komórki pamięci
ht – sygnał wyjściowy w aktualnej chwili czasowej t danej komórki pamięci; jest to sygnał wyjściowy neuronu ukrytego podawany na warstwę wyjściową neuronów sieci.
Komórka przetwarza nieliniowo zarówno aktualny sygnał wejściowy podany na jej wejście jak i sygnały wyjściowe oraz pamięci z chwili poprzedniej wszystkich bloków z którymi jest sprzężona. Struktura przepływu sygnałów w dwu kolejnych chwilach czasowych dla sieci LSTM dla jednej komórki może być przedstawiona jak na rys. 10.9.
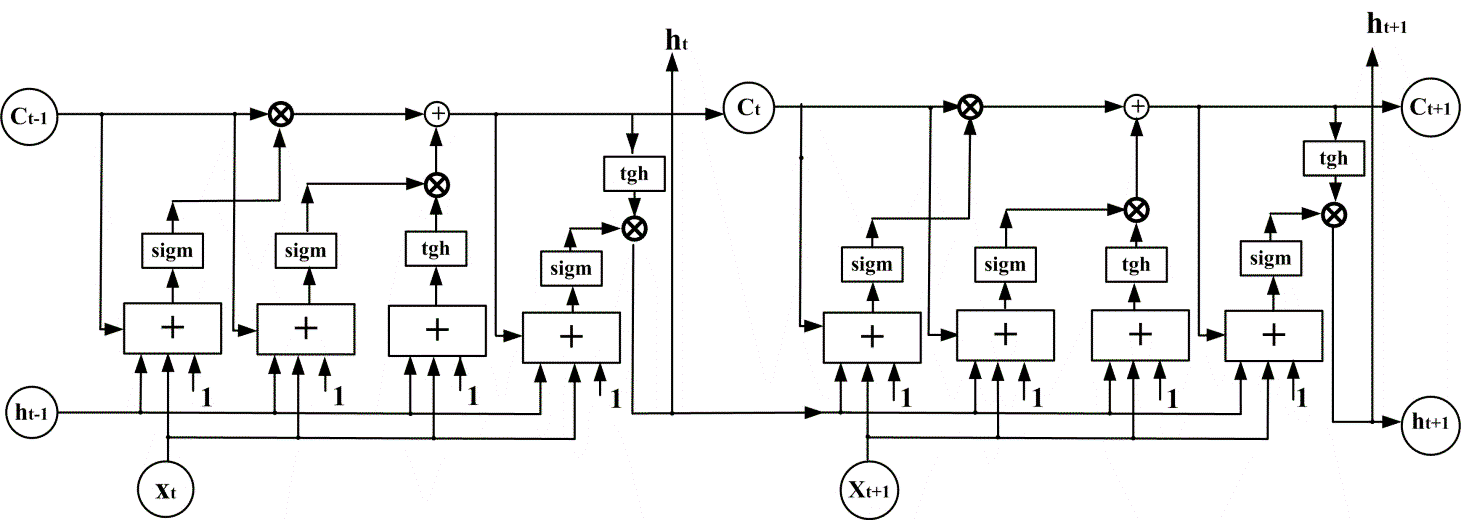
Bardzo istotną rolę w przetwarzaniu sygnałów odgrywają bramki multiplikatywne, oznaczone symbolem ×. Górna bramka z lewej strony komórki jest sterowaną bramką (zaworem) pamięci. Decyduje o tym jaka część pamięci z poprzedniej chwili czasowej przejdzie do chwili następnej. Stanowi zatem regulowany system zaworowy, który przepuszcza w określonym stopniu (od zera do 1) informację zawartą w pamięci z chwili poprzedniej. O poziomie przejścia tej zawartości decyduje sygnał wytworzony przez warstwę neuronową sigmoidalną, widoczną z lewej strony modelu.
Druga bramka (symbol środkowy ×) stanowi następny regulowany zawór nowej pamięci i uczestniczy w wytworzeniu zawartości pamięci Ct dla aktualnej chwili czasowej. Stanowi sterowane połączenie nowo wytworzonego stanu pamięci i pamięci poprzedniej Ct-1, która została przepuszczona przez zawór pierwszy. Połączenie tych informacji następuje w bloku sumatora. W efekcie takiej operacji stara zawartość pamięci Ct-1 zostaje zamieniona na nową Ct.
Poszczególne zawory mają swoje wymuszenia i sygnały wyjściowe. Zawór pamięci jest sterowany poprzez jednowarstwową sieć neuronową o sigmoidalnej (jedno-polarnej) funkcji aktywacji. Sygnały wejściowe dla tej warstwy stanowią: Xt – sygnał wejściowy w aktualnej chwili czasowej t, Ct-1 – sygnał pamięci z chwili t-1 poprzedniej komórki pamięci, ht-1 – sygnał wyjściowy z chwili t-1 poprzedniej komórki pamięci oraz sygnał polaryzacji. Sumacyjny sygnał wyjściowy zaworu pamięci po przetworzeniu sigmoidalnym mnożony jest z sygnałem pamięci z chwili poprzedniej i stanowi dla niej współczynnik z jakim poprzednia pamięć przechodzi do następnej chwili czasowej.
Drugi zawór reprezentowany przez środkowy mnożnik × decyduje o nowym stanie pamięci Ct w chwili t i jest nazywany zaworem nowej pamięci. Składa się z dwu równolegle działających warstw neuronowych. Pierwsza warstwa sigmoidalna jedno-polarna przyjmuje identyczne wymuszenia jak warstwa neuronowa w zaworze pamięci (Xt, Ct-1, ht-1 i polaryzacja) i stanowi przetworzoną zawartość starej pamięci. Druga warstwa operuje jedynie sygnałami Xt, ht-1 oraz polaryzacją, a więc nie zależy od zawartości starej pamięci. Funkcja aktywacji tej warstwy jest sigmoidą bipolarną realizowaną przez funkcję tangensa hiperbolicznego. Mnożnik decyduje o wpływie starej pamięci na stan wyjściowy tego zaworu, który będzie następnie dodany do zawartości starej pamięci wychodzącej z bloku pamięci (symbol sumatora) tworząc aktualny (w chwili t) stan pamięci Ct.
Ostatnią operacją komórki pamięciowej jest wytworzenie sygnału wyjściowego ht w aktualnej chwili czasowej t. Sygnał wyjściowy komórki jest iloczynem dwu sygnałów: aktualnego sygnału pamięci Ct przepuszczonego przez funkcję sigmoidalną bipolarną oraz sygnału wyjściowego z warstwy neuronowej zasilonej poprzez Xt, ht-1 oraz polaryzację. System ten stanowi zawór wyjściowy komórki, decydujący o tym jak duża porcja nowej pamięci zostanie przekazana na wyjście komórki, czyli sygnału komórki, który zasili komórkę w następnej chwili czasowej.
W efekcie wysterowania poszczególnych zaworów możliwe jest przepuszczenie lub zablokowanie określonej porcji informacji z chwil poprzednich. Na rys. 10.10 zilustrowano możliwy wpływ informacji dostarczonej do sieci w chwili t1 na stan komórki w następnych chwilach czasowych. Symbol „o” oznacza pełne otwarcie zaworu a symbol „–„ pełne zamknięcie. Stan wyjścia komórek w poszczególnych chwilach czasowych w zależności od informacji z chwili t1 jest funkcją otwarcia lub zamknięcia odpowiednich zaworów i ilustrowany ciemnym stanem węzła (informacja przechodzi) lub jasnym (przepływ informacji zablokowany).

10.2.3 Uczenie sieci LSTM
W procesie uczenia doborowi podlegają wagi poszczególnych połączeń sieci poprzez minimalizację funkcji błędu na danych uczących w postaci par (wielkość wejściowa x i wielkość zadana na wyjściu d) określonych w kolejnych chwilach czasowych. Minimalizacja odbywa się metodą gradientową przy generacji gradientu poprzez zastosowanie propagacji wstecznej. Sygnały wejściowe przesyłane są najpierw wprzód (w obrębie przyjętego okna czasowego T) a następnie błąd na wyjściu w poszczególnych chwilach czasowych przesyłany jest w kierunku odwrotnym (od wyjścia do wejścia). Na tej podstawie generowane są składniki gradientu względem poszczególnych wag sieci, podobnie jak odbywało się to w klasycznych sieciach neuronowych.
Przyjmijmy oznaczenia wskaźnikowe jak na rys. 10.8. Poszczególne warstwy neuronowe charakteryzowane są poprzez macierze wagowe opisane za pomocą dwu wskaźników: pierwszy pochodzi od numeru przypisanego warstwie, drugi od symbolu wielkości wejściowej dla tej warstwy. Przykładowo w1h oznacza macierz wagową pierwszego zaworu przetwarzającą sygnały wyjściowe komórki ht-1 z poprzedniej chwili wagowej. Funkcja sigmoidalna oznaczona jest symbolem sigm a symbol tgh oznacza funkcję tangensa hiperbolicznego. Wektory sygnałowe w poszczególnych punktach komórki są wyrażone wzorami [58]
| \( \mathbf{y}_1=\operatorname{sigm}\left(\mathbf{W}_{1 c} \mathbf{c}_{\mathbf{t}-1}+\mathbf{W}_{1 h} \mathbf{h}_{t-1}+\mathbf{W}_{1 x} \mathbf{x}_t+\mathbf{w}_{10}\right) \) | (10.19) |
| \(\mathbf{y}_2=\operatorname{sigm}\left(\mathbf{W}_{2 c} \mathbf{c}_{t-1}+\mathbf{W}_{2 h} \mathbf{h}_{t-1}+\mathbf{W}_{2 x} \mathbf{x}_t+\mathbf{w}_{20}\right) \) | (10.20) |
| \(\mathbf{y}_3=\operatorname{tgh}\left(\mathbf{W}_{3 h} \mathbf{h}_{t-1}+\mathbf{W}_{3 x} \mathbf{x}_t+\mathbf{w}_{30}\right) \) | (10.21) |
| \(\mathbf{y}_4=\operatorname{sigm}\left(\mathbf{W}_{4 c} \mathbf{c}_t+\mathbf{W}_{4 h} \mathbf{h}_{t-1}+\mathbf{W}_{4 x} \mathbf{x}_t+\mathbf{w}_{40}\right) \) | (10.22) |
Na tej podstawie tworzone są: stan pamięciowy komórki ct oraz sygnał wyjściowy komórki ht (oba w chwili t). Są one określone wzorami
| \(\mathbf{c}_t=y_2 \cdot y_3+c_{t-1} y_1\) | (10.23) |
| \(\mathbf{h}_t=\boldsymbol{y}_4 \cdot \operatorname{tgh}\left(\mathbf{c}_t\right)\) | (10.24) |
Przetwarzanie wsteczne sygnałów odbywa się w identyczny sposób jak w metodzie klasycznej propagacji wstecznej (odwrócenie kierunku przepływu przy tych samych wartościach wag gałęzi liniowej i zastąpieniu funkcji aktywacji poprzez wartość pochodnej w punkcie pracy sieci o normalnym kierunku przepływu). W przypadku węzła realizującego mnożenie korzysta się z zależności pochodnej iloczynu, zgodnie z którą, jeśli sygnał y jest iloczynem dwu sygnałów v1 i v2, \(y=v_1(w) \cdot v_2(w)\) to
| \(\frac{d y}{d w}=v_1 \frac{d v_2}{d w}+v_2 \frac{d v_2}{d w}\) | (10.25) |
Pełna informacja o gradiencie jest sumą pochodnych po wszystkich krokach czasowych wykonanych wewnątrz okna pomiarowego T. W uczeniu wykorzystuje się z reguły metodę stochastyczną największego spadku z momentem rozpędowym (SGD) lub metodykę ADAM.
10.2.4 Przykład zastosowania sieci LSTM w prognozowaniu zanieczyszczeń atmosferycznych
W tym punkcie pokazane zostanie zastosowanie sieci LSTM do prognozowania godzinnych zmian poziomu 4 zanieczyszczeń atmosferycznych (PM10, SO2, NO2, and ozon) [47]. Prognozowanie poziomu zanieczyszczeń należy do zadań trudnych, ze względu na znaczne różnice występujące między sąsiednimi godzinami tego samego dnia. Widać to wyraźnie na wartościach statystycznych dotyczących tych zanieczyszczeń dla danych zmierzonych w Warszawie (dzielnica Ursynów) pokazanych w tabeli 10.2.
Table 10.2. Parametry statystyczne zanieczyszczeń atmosferycznych poddanych predykcji
|
|
PM10 |
SO2 |
NO2 |
Ozon |
|
Mean \([ \mu g/ m^3 ] \) |
33.56 |
9.89 |
24.82 |
48.43 |
|
Std/mean [%] |
78.20 |
88.82 |
71.92 |
64.20 |
|
Max \([ \mu g/ m^3 ] \) |
414.91 |
57.84 |
203.86 |
189.12 |
|
Min \([ \mu g/ m^3 ] \) |
0.70 |
0.71 |
0.42 |
0.09 |
W rozwiązaniu problemu predykcji zastosowano sieć LSTM o 4 neuronach wyjściowych (każdy odpowiedzialny za predykcję określonego typu zanieczyszczenia). Jako wejście dla sieci (wektor x) zastosowano następujące wielkości: PM10, SO2, NO2, OZON, szybkość wiatru, kierunek wiatru, temperaturę, promieniowanie słoneczne, wilgotność, składowe prędkości wiatru w osi x i y (wszystkie znane wielkości z godziny poprzedzającej predykcję). Liczba neuronów ukrytych zastosowana w strukturze sieci była równa 500. W uczeniu zastosowano metodę ADAM.
Dla zwiększenia dokładności predykcji zastosowano zespół sieci złożony ze struktur LSTM różniących się liczbą neuronów ukrytych (od 300 do 700), wartością „dropout ratio” jak również składem zbioru danych uczących (wybieranych losowo z bazy danych) dla każdej sieci. Procedurę uczenia i testowania na tym samym zbiorze danych testujących powtórzono 5 razy. Wynik zespołu jest średnią arytmetyczną wyników poszczególnych jednostek LSTM.
W tabeli 10.3 przedstawiono wyniki działania systemu przy predykcji pyłów PM10. Wyniki dotyczą takich miar jakości, jak MAPE, MAE, RMSE, MPSE oraz R. MPSE jest zmodyfikowaną wersją MAPE, w której porównuje się normy wektora błędów w stosunku do normy wielkości rzeczywistych – tego typu modyfikacja jest istotna przy bardzo małych (zbliżonych do zera wartości rzeczywistych zanieczyszczenia). Pozytywny wpływ zespołu jest widoczny, choć niezbyt imponujący.
Tabela 10.3. Wyniki predykcji pyłu PM10 (predykcja z wyprzedzeniem godzinnym) [47]
|
|
MAPE [%] |
MAE \([ \mu g/ m^3 ] \) |
RMSE \([ \mu g/ m^3 ] \) |
MPSE [%] |
R |
|
Średnia członków zespołu |
13.86 |
4.27 |
7.40 |
11.91 |
0.9649 |
|
Zespół |
13.70 |
4.11 |
7.36 |
11.74 |
0.9653 |
Na rys. 10.11 przedstawiono wyniki predykcji porównane z wartościami prawdziwymi (wykres górny) oraz błąd względny predykcji w poszczególnych godzinach.
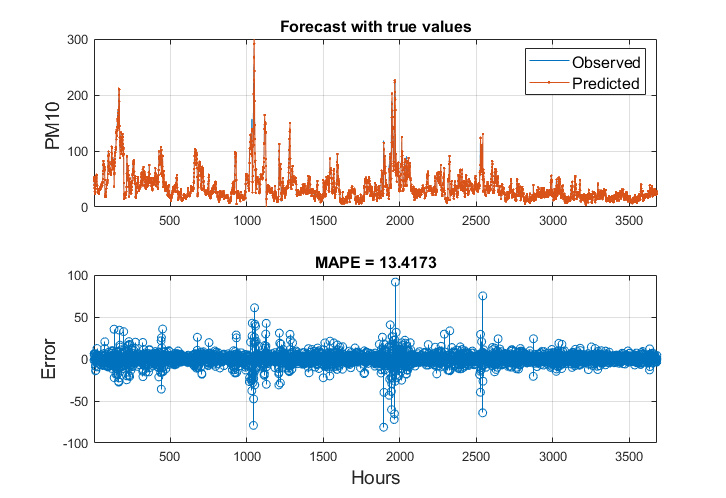
Na rys. 10.12 przedstawiono nałożone na siebie wykresy wielkości rzeczywistych i prognozowanych PM10 dla 120 godzin dla uwypuklenia szczegółów przebiegów podlegających prognozowaniu.
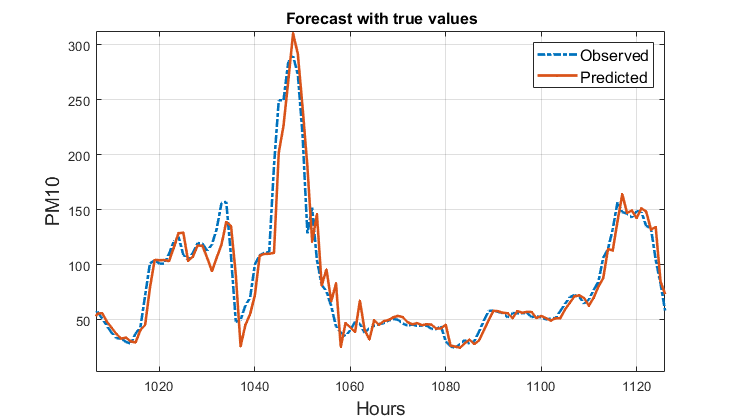
W tabeli 10.4 przedstawiono wyniki predykcji dotyczące pozostałych 3 rodzajów zanieczyszczeń. Podobnie jak w przypadku PM10 wyniki zespołu są na wyższym poziomie niż średnia wyników indywidualnych sieci bez ich fuzji.
Tabela 10.4. Wyniki statystyczne dotyczące predykcji zanieczyszczeń SO2, NO2 ozonu in przy prognozie z wyprzedzeniem 1-godzinnym
|
Zanieczyszczenie |
|
MAPE [%] |
MAE \([ \mu g/ m^3 ] \) |
RMSE \([ \mu g/ m^3 ] \) |
MPSE [%] |
R |
|
SO2 |
Średnia członków zespołu |
23.48 |
2.22 |
4.40 |
22.20 |
0.8488 |
|
Zespół |
22.82 |
2.15 |
4.30 |
21.52 |
0.8556 |
|
|
NO2 |
Średnia członków zespołu |
19.95 |
4.21 |
6.72 |
17.62 |
0.9157 |
|
Zespół |
19.53 |
4.13 |
6.63 |
17.30 |
0.9180 |
|
|
Ozon |
Średnia członków zespołu |
26.00 |
5.81 |
8.62 |
11.24 |
0.9592 |
|
Zespół |
25.93 |
5.79 |
8.60 |
11.31 |
0.9593 |
Ostatni eksperyment dotyczył predykcji średniodobowych wartości zanieczyszczeniaPM10. Zastosowano zespół 5 sieci LSTM zbudowany na identycznej zasadzie jak w przypadku prognozy godzinnej. Wyniki statystyczne poszczególnych członków zespołu przed integracją i po integracji w zespole przedstawiono w tabeli 10.5. Tym razem widoczna jest znacząca poprawa wyników zespołu w stosunku do średniej jej członków przed fuzją. Przykładowo, wartość błędu MAPE została zredukowana z 8.11% do 7.29% (ponad 10% poprawa względna).
Table 10.5. Wyniki statystyczne predykcji średniodobowej dla pyłu PM10
|
Zanieczyszczenie |
|
MAPE [%] |
MAE \([ \mu g/ m^3 ] \) |
RMSE \([ \mu g/ m^3 ] \) |
MPSE [%] |
R |
|
PM10 |
Średnia członków zespołu |
8.11 |
2.98 |
3.23 |
9.03 |
0.7975 |
|
Zespół |
7.29 |
2.33 |
2.88 |
8.84 |
0.8394 |