Podręcznik Grafika komputerowa i wizualizacja

Zaproponowane macierze rzutowania, zarówno perspektywicznego jak równoległego mają jedną zerową kolumnę lub wiersz.

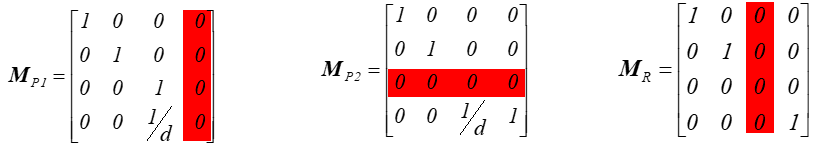
Oznacza to że nie jest możliwe wyznaczenie macierzy odwrotnej. Wszystkie te macierze są nieodwracalne. Rzutowanie jest operacją nieodwracalną. W rzutowaniu obrazem każdego punktu leżącego na prostej (promieniu) rzutującej jest jeden (i ten sam) punkt na rzutni. Czyli nie jest możliwe odtworzenie trzeciego wymiaru tylko i wyłącznie na podstawie rzutu obiektu.

Często do następnych operacji (na przykład do eliminacji elementów zasłoniętych) niezbędna jest informacja o trzecim wymiarze (odległości od obserwatora - głębokości). Rozwiązanie tego problemu przynosi operacja nazywana przekształceniem perspektywicznym (a nie rzutowaniem). Jest to operacja, która pozwala wyznaczyć rzut perspektywiczny i jednocześni daje informację o odległości.

Jeśli rozpatrzymy znormalizowaną bryłę widzenia perspektywicznego – ostrosłup ścięty, to promienie rzutujące tworzą pęk prostych w wierzchołku tego ostrosłupa. Można dokonać przekształcenia, które przekształci ostrosłup ścięty na prostopadłościan (rys.5.11). Wtedy pęk prostych (promieni rzutujących) stanie się zbiorem prostych równoległych. A to oznacza, że po takim zniekształceniu przestrzeni wszystkie punkty leżące na prostej rzutującej będą miały jednakowe współrzędne odpowiadające współrzędnym rzutu.

Operacja ta wymaga normalizacji współrzędnych. Współrzędne punktów ostrosłupa ściętego muszą spełniać następujące warunki:

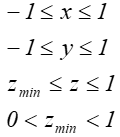
Macierz przekształcenia perspektywicznego ma postać:

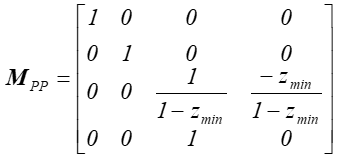
Zaś zależność między współrzędnymi punktu i jego rzutu ma teraz postać.:
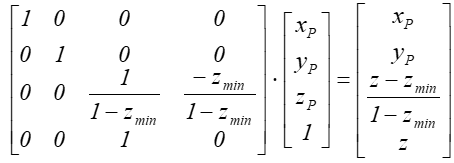         po normalizacji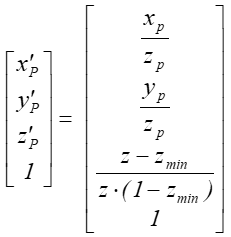 

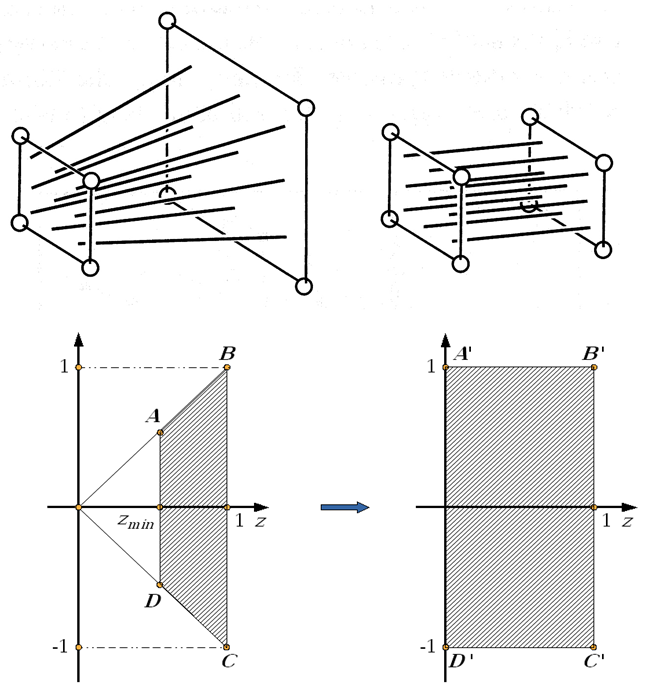
      Rys. 5.11. Przekształcenie perspektywiczne.  Na podstawie [6].

Macierz przekształcenia perspektywicznego wymaga normalizacji operacji. Wynik na rysunku jest podany z uwzględnieniem normalizacji.

 Jak widać współrzędne x_P i y_P obrazu punktu odpowiadają współrzędnym rzutu perspektywicznego przy założeniu, że środek rzutowania jest w początku układu współrzędnych. Jednocześnie współrzędna z obrazu daje informację o położeniu względem osi OZ. Warto zwrócić uwagę na fakt, że przekształcenie wartości głębokości jest operacją nieliniową, ale zachowującą porządek na prostej, co w zupełności wystarcza do oceny głębokości.