Podręcznik Grafika komputerowa i wizualizacja

W zasadzie można byłoby stwierdzić, że oczekiwane właściwości końcowe projektu i wyobraźnia projektantów powinna być jedynymi ograniczeniami narzuconymi na proces wspomagania projektowania. W takim razie przez obiekt graficzny należałoby rozumieć cokolwiek, co da się narysować przy pomocy komputera. Wydaje się jednak, że celem nie jest jedynie swoboda projektowania, ale efekt końcowy, jakim jest realizacja fizyczna danego obiektu. I z tego powodu bardzo często wprowadza się pewne ograniczenia reprezentacji. Ograniczenia, które nie ograniczając wyobraźni projektanta powinny, wbrew pozorom, ułatwić mu pracę.

Najczęściej rozpatrywany zestaw cech jakie będą  oczekiwane od brył, które są rozpatrywane przez systemy modelowania geometrycznego:

Zaproponowany zestaw właściwości bryły jest pewnym kompromisem między swobodą projektowania a zastosowaniami praktycznymi, kompromisem, który daje przy tym możliwość efektywnego wspomagania projektowania. Przykładem jak należy rozumieć ten kompromis jest jednorodność topologiczna. Z jednej strony nie ma w zasadzie żadnych przeciwwskazań w grafice komputerowej aby tworzyć obiekty niejednorodne (np. krzesło w postaci trójwymiarowego sześciennego siedziska połączonego z dwuwymiarowym prostokątnym oparciem). Ale jednocześnie ujednolicenie opisu może uprościć podejście do różnie definiowanych elementów. Natomiast jeśli popatrzymy na problem od strony praktycznej; technologicznie realizacyjnej, to okaże się, że problem w zasadzie nie istnieje ponieważ żyjemy wśród obiektów trójwymiarowych jednorodnych topologicznie i praktyczne wykonanie prostokątnego oparcie dla rozpatrywanego krzesła i tak będzie wymagało określenia trzeciego wymiaru – jego grubości. Jeśli już nawet dla spełnienia wizji projektanta jest niezbędne istnienie niejednorodności topologicznej to prościej jest założyć, że w ramach jednej bryły zachowujemy jednorodność i w ostateczności dopuszczamy zestawienie różnych brył w ramach jednego procesu. Chociaż i tak w efekcie końcowym na etapie technologii zostanie to ujednolicone. Podobnie problem występuje ze sztywnością bryły. Sztywność nie musi oznaczać niezmienności kształtu, ale raczej niezmienność struktury lub budowy obiektu. Pręt stalowy może podlegać pewnym drobnym zmianom kształtu (ugięcie, skręcenie) bez zmiany struktury czy budowy. Dopiero przyłożenie większej siły powoduje np. jego zgięcie czy złamanie. W tym kontekście gumka do ścierania może być, w pewnych sytuacjach, traktowana jako bryła sztywna.

 Elementem opisu właściwości bryły, na który warto zwrócić uwagę jest domknięcie bryły. To co widzimy obserwując dowolny przedmiot jest efektem odbicia światła od powierzchni tego przedmiotu. Jeśli zostanie on przekrojony to zobaczymy powierzchnię przekroju – to znaczy będzie to nowy brzeg powstały przecięcia. Powierzchnia brzegu obiektu jest więc bardzo istotna w procesie rysowania – wizualizacji obiektu.

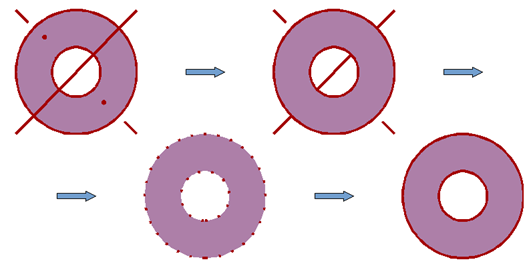
Rys.6.1. Domknięcie – regularyzacja zbioru.

Proces rozwiązania problemu domknięcia bryły nazywany jest regularyzacją zbioru (rys. 6.1). Jeśli rozpatrzymy dowolny obiekt jako pewien zbiór punktów to można wyróżnić punkty wewnętrzne tworzące zbiór otwarty, punkty brzegowe (punkty, których odległość zarówno od obiektu jak i jego uzupełnienia jest równa zeru) oraz zbiór domknięty, zawierający wszystkie jego punkty wewnętrzne i wszystkie brzegowe. Rysunek pokazuje regularyzację zbioru. Kolejne etapy to: domknięcie poprzez przejęcie do wnętrza ewentualnych punktów zdefiniowanych jako brzeg (np. w wyniku jakiejś operacji na zbiorach), a które w rzeczywistości znajdują się we wnętrzu. Otwarcie zbioru pozwalające wyeliminować punkty brzegowe niepołączone z wnętrzem. Ponowne domknięcie dające regularyzację zbioru.

Można zastanowić się jak efektywnie opisać bryłę? Jakie jej cechy wykorzystać?

 Biorąc pod uwagę te dwa, różne podejścia do opisu bryły, wyróżnia się cztery podstawowe metody reprezentacji obiektów najczęściej stosowane w grafice komputerowej: