Podręcznik Grafika komputerowa i wizualizacja
Rozdział 7. MODELOWANIE KRZYWYCH I POWIERZCHNI
7.5. Krzywe B-sklejane
Krzywa
B-sklejana jest definiowana jako kombinacja liniowa funkcji sklejanych ![]() o współczynnikach
odpowiadających punktom kontrolnym (punktom de Boora). Funkcje sklejane są
przedziałami stopnia m, co nie jest
związane z liczbą punktów tak jak w przypadku krzywych Béziera. Oznacza to
rzeczywiście uniezależnienie stopnia wielomianu opisującego krzywą (oczywiście
przedziałami w tym przypadku) od liczby punktów kontrolnych.
o współczynnikach
odpowiadających punktom kontrolnym (punktom de Boora). Funkcje sklejane są
przedziałami stopnia m, co nie jest
związane z liczbą punktów tak jak w przypadku krzywych Béziera. Oznacza to
rzeczywiście uniezależnienie stopnia wielomianu opisującego krzywą (oczywiście
przedziałami w tym przypadku) od liczby punktów kontrolnych.
Krzywa B-sklejana opisana jest jako:
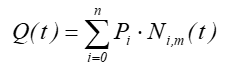
punkty kontrolne Pi nazywane są punktami de Boora.
Funkcje sklejane ![]() określa się
rekurencyjnie:
określa się
rekurencyjnie:
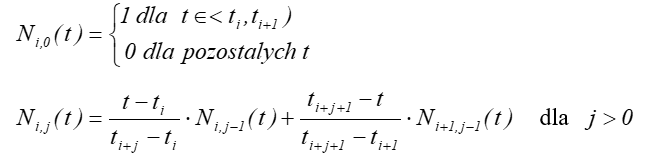
Funkcje
sklejane ![]() są przedziałami
wielomianami i mają następujące właściwości:
są przedziałami
wielomianami i mają następujące właściwości:
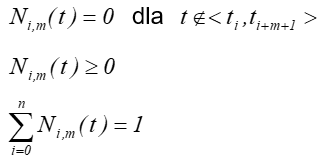
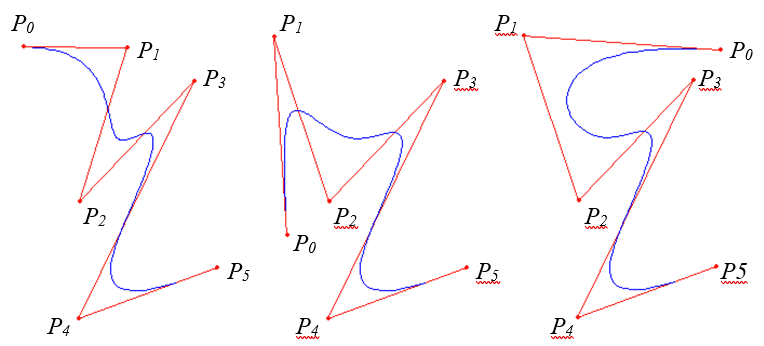
Rys.7.9. Przykłady
krzywych B-sklejanych. Zmiana położenia
punktów kontrolnych P0 i P1 powoduje
lokalne (tylko !) zmiany kształtu krzywej. Nie wpływa to na
kształt pozostałej części krzywej.
Zakłada się, że węzły ti są uporządkowane niemalejąco tzn. ti ≤ ti+1 co oznacza, że mogą istnieć równe węzły (wielokrotne). Przyjmuje się wtedy, że 0/0=0. Takie założenia generalnie definiują krzywą dla węzłów które nie musza być równoodległe. Jednocześnie możliwość dodania (wstawienie) węzła pomiędzy dwa już istniejące, lub zwielokrotnienia węzła daje dodatkowe możliwości wpływania na kształt krzywej. Czasami jednak rozpatruje się krzywe o węzłach równoodległych.
Istnieje algorytm de Boora i Coxa wyznaczania punktów krzywej B-sklejanej (analogiczny do algorytmu de Casteljau dla krzywej Béziera) [3]. Jeśli wyznaczanych jest wiele punktów krzywej to tańszym rozwiązaniem będzie obliczenie współczynników postaci naturalnej wielomianu w kolejnych podprzedziałach i skorzystanie z algorytmu Hornera.
Właściwości krzywych B-sklejanych
Pierwsza właściwość – zerowanie funkcji sklejanej poza przedziałem ![]() jest bardzo istotna
dla modelowania kształtu. Oznacza bowiem lokalność wpływu parametrów (rys.7.9).
Rozpatrzmy podprzedział
jest bardzo istotna
dla modelowania kształtu. Oznacza bowiem lokalność wpływu parametrów (rys.7.9).
Rozpatrzmy podprzedział ![]() dla
dla ![]() niezerowe są tylko funkcje
niezerowe są tylko funkcje ![]() o indeksach i=j-m, j-m+1, j-m+2, j . W takim przedziale wartość Q(t) , a tym samym kształt krzywej,
zależy tylko od punktów kontrolnych Pj-m
, Pj-m+1 , Pj-m+2 , … Pj . Z drugiej strony
punkt kontrolny Pi wpływa
jedynie na fragment krzywej odpowiadający
o indeksach i=j-m, j-m+1, j-m+2, j . W takim przedziale wartość Q(t) , a tym samym kształt krzywej,
zależy tylko od punktów kontrolnych Pj-m
, Pj-m+1 , Pj-m+2 , … Pj . Z drugiej strony
punkt kontrolny Pi wpływa
jedynie na fragment krzywej odpowiadający ![]() .
.
Indeks j zmienia się od 0 do m , natomiast i od 0
do n . Cały zakres takiej krzywej
definiują więc węzły: ![]() . Ale danych jest n+1 punktów kontrolnych (de Boora).
Punkty P0 , P1, P2 , … Pm definiują krzywą dla
. Ale danych jest n+1 punktów kontrolnych (de Boora).
Punkty P0 , P1, P2 , … Pm definiują krzywą dla ![]() , natomiast punkty Pn-m, Pn-m+1, Pn-m+2,…Pn definiują krzywą dla
, natomiast punkty Pn-m, Pn-m+1, Pn-m+2,…Pn definiują krzywą dla ![]() . Węzły
. Węzły ![]() oraz
oraz ![]() nazywane są węzłami
brzegowymi. Jeśli krzywa jest otwarta, to znaczy
nazywane są węzłami
brzegowymi. Jeśli krzywa jest otwarta, to znaczy ![]() , i
, i ![]() oraz
oraz ![]() to krzywa przechodzi
przez końcowe punkty kontrolne, czyli
to krzywa przechodzi
przez końcowe punkty kontrolne, czyli ![]() .
.
Podobnie jak było w przypadku krzywych Béziera, styczne do krzywej w punktach końcowych mają kierunek końcowych odcinków łamanej kontrolnej. Dla krzywej zamkniętej przyjmuje się, że punkty de Boora i węzły kontrolne są cykliczne (Pn=P0).
Jest spełniony warunek wypukłej skorupki (krzywa zawiera się całkowicie w wypukłej skorupce zbudowanej na punktach kontrolnych), ale tylko w sąsiedztwie punktów !
Wymierne krzywe B-sklejane (NURBS)Wymierne krzywe B-sklejane (ang. Non-Uniform Rational B-Splines) to rozwiązanie, które łączy zalety krzywych Béziera i krzywych B-sklejanych. Krzywe te opisane są w sposób następujący:
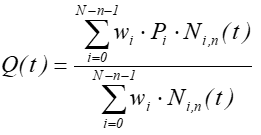
Punkty Pi (de Boora ) są punktami kontrolnymi, wi są wagami tych punktów.
- Krzywe wymierne dają możliwość wykreślenia dowolnej krzywej stożkowej.
- Konstrukcja wykorzystująca funkcje sklejane pozwala opisywać krzywą wielomianami, których stopień jest niezależny od liczby punktów kontrolnych.
- Wpływ punktu kontrolnego na kształt krzywej istnieje tylko w zakresie lokalnym.
- Dodatkowo wagi każdego punktu kontrolnego pozwalają na precyzyjne zmiany kształtu krzywej (też lokalnie).
- Krzywe wymierne są niezmiennicze względem przekształceń obrotu, skalowania i przesunięcia oraz przekształcenia perspektywicznego punktów kontrolnych.
