Podręcznik Grafika komputerowa i wizualizacja: 7.3. Parametryzacja krzywych i powierzchni

Rozdział 7. MODELOWANIE KRZYWYCH I POWIERZCHNI

7.3. Parametryzacja krzywych i powierzchni

Wiele krzywych jest opisanych równaniem uwikłanym postaci . Taka reprezentacja nie daje możliwości kontroli konkretnego fragmentu krzywej.

Wygodnym sposobem opisu krzywych i powierzchni jest opis parametryczny.

Parametryczna reprezentacja krzywych: .

Powierzchni: .

Za pomocą doboru wartości parametru można zdefiniować dowolny fragment krzywej, a kierunek wzrostu parametru jednoznacznie określa np. kierunki stycznych połączonych fragmentów.

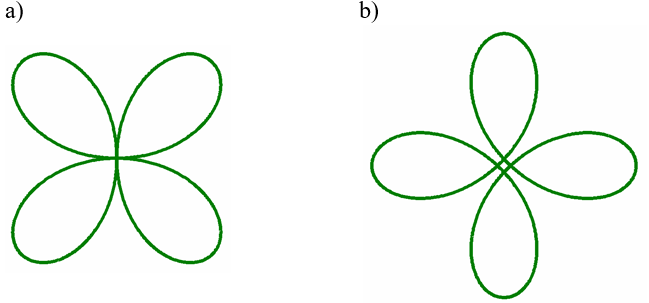
Rys.7.2. Czterolistna koniczyna. Różne reprezentacje parametryczne krzywej .

Przykładowa czterolistna koniczyna jest narysowana na rysunku 7.2 a w postaci rozety czterolistnej o reprezentacji parametrycznej:

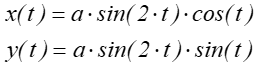dla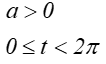

Na rysunku 7.2 b w postaci hipotrochoidy:

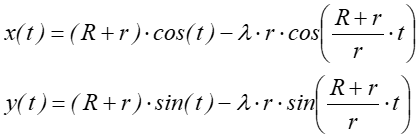dla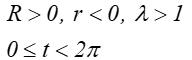

Często stosowany jest opis kształtu powierzchni obiektów wykorzystujący równanie drugiego stopnia. Powierzchnie drugiego stopnia to elipsoida, walec (cylinder), stożek, paraboloida eliptyczna, paraboloida hiperboliczna, hiperboloida jednopowłokowa, hiperbolida dwupowłokowa. Ich równanie uwikłane ma postać:

gdzie Q jest macierzą współczynników postaci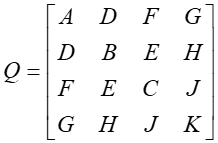

oraz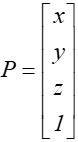

Przy czym dla każdej powierzchni drugiego stopnia jest znana reprezentacja parametryczna. Przykładowa hiperboloida jednopowłokowa, zaprezentowana na rysunku: 7.3, o równaniu uwikłanym postaci 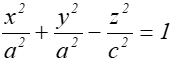, została przedstawiona parametrycznie jako:

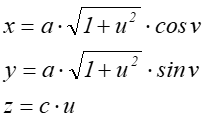dla

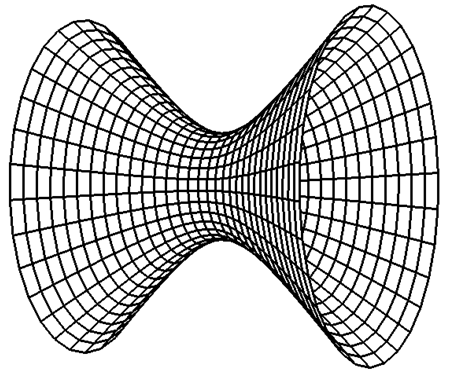
Rys.7.3. Hiperbola jednopowłokowa.

Zalety stosowania powierzchni drugiego stopnia:

Możliwość łatwego wyznaczenia wektora normalnego .
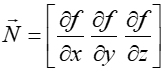Możliwość szybkiego wyznaczenia przecięcia powierzchni z prostą – efektywność stosowania w algorytmach związanych z metodą śledzenia promieni.
Możliwość szybkiego wyznaczenia z na podstawie x i y – przydatne w algorytmach eliminacji elementów zasłoniętych.
Powierzchnia drugiego stopnia jest praktycznie użyteczna w wielu aplikacjach technicznych (wystarczająco skomplikowane kształty).